Module 19 - Applications of Integration

Module 19 - Answers

Lesson 1

Answer 1

19.1.1

Answer 2

19.1.2

[0, 4, 1] x [-5, 15, 1]

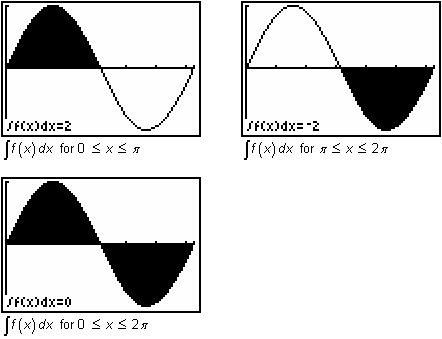
The net area is 4 square units.

Answer 3

19.1.3

The graph shown below is an approximation of the net-area function.

Lesson 2

Answer 1

19.2.1

The total area bounded by y = x³ – 3x² – x + 3 and the x-axis on the interval [0, 4] is 12 square units.

Answer 2

19.2.2

The x-coordinate of the right point of intersection is approximately 1.562.

Answer 3

19.2.3

The area between the two curves is approximately 11.682 square units.

Lesson 3

Answer 1

19.3.1

The length of the curve y = x² between x = -1 and x = 2 is approximately 6.126 units.

Self Test

Answer 1

The net area bounded by f(x) = x³ - 4x² - 4x + 16 and the x-axis is approximately 19.583 square units.

Answer 2

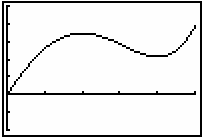
The screen below shows one possible net-area function for f(x) = x³ - 4x² - 4x + 16 over [0, 5].

Answer 3

The total area bounded by f(x) = x³ – 4x² – 4x + 16 and the x-axis over [0, 5] is approximately 32.917 square units.

Answer 4

The area between the two curves f(x) = x² - 1 and g(x) = x is approximately 1.863 square units.

Answer 5

The length of the curve f(x) = sin x between x = 0 and x = 2

is approximately 7.640 units.

Answer 6

The integral

gives the length of f(x) = tanx between x = 0 and x =

/4.