A restatement of the Fundamental Theorem of Calculus is presented in this lesson along with a corollary that can be used to evaluate definite integrals analytically.

Restating the Fundamental Theorem of Calculus

You have discovered the Fundamental Theorem of Calculus in the context of finding areas under a curve but a more general version of this theorem can be proved without an appeal to area. The following is a restatement of the theorem.

If f is continuous on [a, b] and c is any constant in [a, b], then the function

has a derivative at every point in [a, b], and the derivative is

That is, the derivative of a definite integral of f whose upper limit is the variable x and whose lower limit is a constant equals the function f evaluated at x. This is true regardless of the value of the constant lower limit c. As long as c = a, x > a and f(t) is positive on [a, b], the function named F is the same as the area function that was previously explored.

Using the Restated Theorem

The restatement of the theorem may be used to evaluate :

• Clear all functions and turn off all scatter plots in the Y= editor.
• Enter Y₁ = fnInt(sin(T),T,0,X).
• Enter Y₂ = nDeriv(Y₁,X,X).
• Enter Y₃ = sin(X).
• Unselect Y₁.

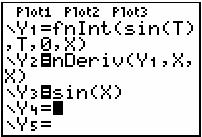
• Select 7:ZTrig from the ZOOM menu.
• Trace on Y2 and Y3 to show the graphs appear to be the same.

Changing Xres The graphs are rather slow to develop because the calculator computes definite integrals and numeric derivatives for each pixel if Xres is 1. You can speed up the graphing somewhat by changing Xres to 2 in the WINDOW settings. The calculator uses every other pixel when Xres = 2.

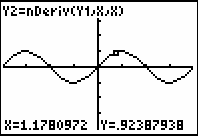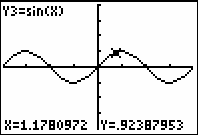18.3.1 Use the restatement of the Fundament Theorem of Calculus to evaluate , and then support your answer with the TI-83.

Click here for the answer.

18.3.2 Predict the following derivative. Check your answer with the TI-83. Hint: You will have to use the chain rule.

Click here for the answer.

18.3.3 Evaluate the following derivative and support your answer with the TI-83.

Click here for the answer.

18.3.4 Find a more general version of the Fundamental Theorem of Calculus by predicting the following derivative.

Click here for the answer.

Using a Corollary of the Fundamental Theorem of Calculus

The following corollary of the Fundamental Theorem of Calculus gives a method for evaluating a definite integral.

Corollary

If f is continuous on [a, b], then

The function F is called an antiderivative of the function f.

18.3.5 Use the corollary to predict the value of , then check your work with the TI-83.

Click here for the answer.

Notice the difference between the derivative of the integral, , and the value of the integral The chain rule is used to determine the derivative of the definite integral. The value of the definite integral is found using an antiderivative of the function being integrated, as stated in the corollary.