In this lesson you will find functions that represent the area under various curves by experimenting and identifying patterns. You will use fnInt to approximate areas and gather data. You will continue your investigation to find the relationship between an area function and the corresponding original curve.

An Area Function for y = x²

You are going to find the area under the curve f(x) = x² between x = 0 and x = b for various values of b. A pattern should emerge that will allow you to write a generalized area function.

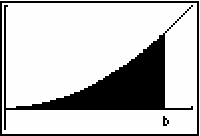
Finding Area

Recall from Module 17 that the area under the curve f(x) = x² between x = 0 and x = 1 was found to be 1/3 using the Definite Integral command.

Find the area under the curve f(x) = x² between x = 0 and x = 2.

• Enter the command fnInt(X², X, 0, 2).

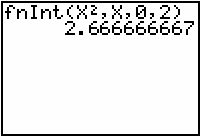
• Convert the answer to a fraction by pressing   .

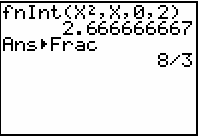
In fact, the exact area under f(x) = x² between x = 0 and x = 2 is square units.

Illustrate the area using the f(x)dx function in the CALC menu of the Graph screen using a [0, 2, 1] x [-1, 4, 1] window.

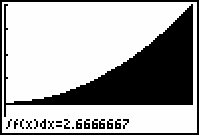
Finding a Formula for Area

Find the area under the curve f(x) = x² between x = 0 and x = 3.

Rather than retyping the entire fnInt command, press to recall the last fnInt command and edit the last parameter in the command by using the arrow keys to place the cursor at the desired position.

Find the area between x = 0 and x = 4. Convert to a fraction.

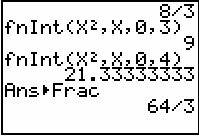
Examine the pattern of the areas as the interval becomes larger.

18.1.1 Predict the area under the curve f(x) = x² between x = 0 and x = 5 then use your calculator to check your prediction. Click here for the answer.

18.1.2 Based on the previous results, find an algebraic formula that generalizes the area under the curve f(x) = x² between x = 0 and x = b.

Click here for the answer

Using Different Variables

The area formula, is a function of b because it gives the area under the function f(x) = x² between x = 0 and x = b, where b is the quantity that varies. This area function could be described using function notation as .

Notice that A and f can both be thought of as functions of the same variable x. The function f evaluated at x yields the y-coordinate of the point (x, f(x)), which lies on the graph of f. If x is positive, the function A evaluated at x yields the area under the graph of f between 0 and the point x on the t-axis. This is illustrated in the diagram below.

Finding Other Area Functions

Definite integrals can be used to find area functions under other curves.

Find the function that gives the area under the curve f(x) = x³ between x = 0 and x = b, where b0.

• Clear the Home screen.
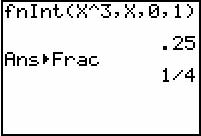
• Find the area under the curve f(x) = x³ between x = 0 and x = 1.
• Convert the result to a fraction.

18.1.3 Find the area under the curve f(x) = x³ between x = 0 and x = b for b = 2, 3, 4, and 5. Fill in the table below and then enter the generalized formula in the last column. State the area function associated with the curve. It will be helpful to write each area as a fraction with the common denominator of 4.

Click here for the answer.

18.1.4 Use the definite integral command to find areas under the curve f(x) = x⁴ between x = 0 and x = b for various positive values of b. Find the area function associated with f(x) = x⁴.

Click here for the answer.

18.1.5 Complete the following table with the curve function whose area function is given.

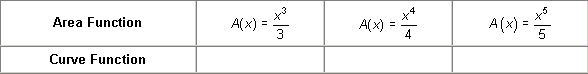
Click here for the answer

18.1.6 Describe the relationship between the area function A and the curve function f.

Click here for the answer.

The Fundamental Theorem of Calculus

If you noticed that the derivative of the area function is the curve function, you have discovered the Fundamental Theorem of Calculus. The theorem states that the derivative of the area function is the curve function, , and it provides the means to solve a wide variety of real world problems that have no apparent relationship to area under the curve.