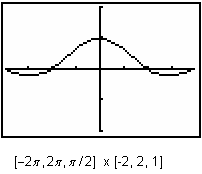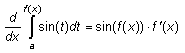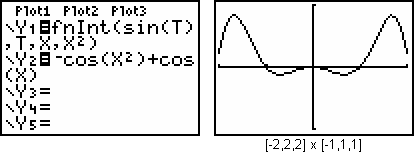|
Module 18 - Answers
|
|
|
|
Lesson 1
|
|
|
|
Answer 1
|
|
|
18.1.1
The area under the curve between x = 0 and x = 5 is
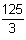 .
.
|
|
|

|

|
|
Answer 2
|
|
|
18.1.2 The area under the curve f(x) = x2 between x = 0 and x = b is given by
 .
.
|
|
|

|

|
|
Answer 3
|
|
|
18.1.3
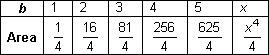
The area function associated with f(x) = x3 is
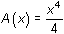 .
.
|
|
|

|

|
|
Answer 4
|
|
|
18.1.4 The function for the area under f(x) = x4 between 0 and x is
 .
.
|
|
|

|

|
|
Answer 5
|
|
|
18.1.5

|
|
|

|

|
|
Answer 6
|
|
|
|
18.1.6
The derivative of the area function A is the curve function f.
|
|
|

|

|
|
Lesson 2
|
|
|
|
Answer 1
|
|
|
18.2.1

|
|
|

|

|
|
Answer 2
|
|
|
18.2.2
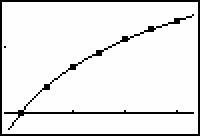

Notice that the coefficient of lnx is approximately 1 and the constant is approximately 0, as denoted by scientific notation E-4.
|
|
|

|

|
|
Answer 3
|
|
|
18.2.3

|
|
|

|

|
|
Answer 4
|
|
|
18.2.4
The derivative of the area function
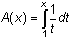 is the curve function, or in other words
is the curve function, or in other words
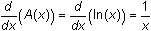 .
.
|
|
|

|

|
|
Answer 5
|
|
|
18.2.5
The area function increases at an increasing rate. It is concave upward.
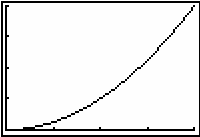
|
|
|

|

|
|
Lesson 3
|
|
|
|
Answer 1
|
|
|
18.3.1 The derivative of this integral function is sin(x)/x.
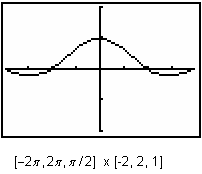
|
|
|

|

|
|
Answer 2
|
|
|
18.3.2 If
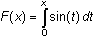 , then
, then
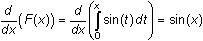 and
and
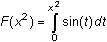 . By the chain rule,
. By the chain rule,
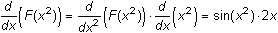 . Thus,
. Thus,
 .
.
[-2, 2, 1] x [-5, 5, 1]
|
|
|

|

|
|
Answer 3
|
|
|
|
18.3.3
|
|
|

|

|
|
Answer 4
|
|
|
18.3.4
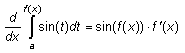
|
|
|

|

|
|
Answer 5
|
|
|
18.3.5 -cos(x) is an antiderivative of sin(x), so the integral equals -cos(
 ) - (-cos(0))=2.
) - (-cos(0))=2.
|
|
|

|

|
|
Answer 6
|
|
|
18.3.6
|
-cos(x2) - (-cos(x))= -cosx2 + cosx |
| |
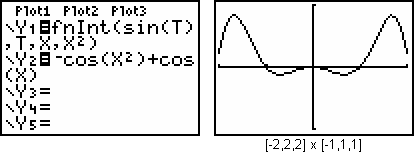 |
|
|
|

|

|
|
Self Test
|
|
|
|
Answer 1
|
|
|
The area function is 
|
|
|
|
Answer 2
|
|
|
|
The derivative of the area function with respect to x is 3x2 which is f(x).
|
|
|
|
Answer 3
|
|
|
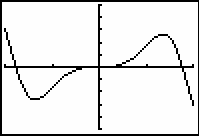
The graph of the area function has the shape shown below.
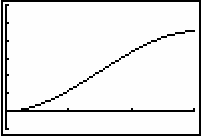
|
|
|
|
Answer 4
|
|
|

|
|
|
|
Answer 5
|
|
|
|
sin(x2) - sin(x)
|
|
|

|
©Copyright
2007 All rights reserved. |
Trademarks
|
Privacy Policy
|
Link Policy
|
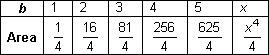
![]() .
.