A calculator-produced graph cannot provide confirmation that your analytic work is correct because calculator graphs are sometimes flawed. However, graphs that match can be considered support that your work is probably correct. In this lesson you will use rules to find derivatives of several functions and then use your TI-83 to provide support for your results.
The Power Rule
One of the most basic functions is a power of x. Its derivative can be found by using the Power Rule. The Power Rule says
Finding a Tangent Line
The Power Rule can be used to find the derivative of the function y = x3. The derivative can then be used to find the slope and the equation of the line tangent to y = x3 at the point (1,1). The easiest way to write the equation is to use the by using the
point-slope form of a line.
![]()
![]()
The point-slope form of the equation for the line through the point (x1, y1) with slope m is
![]()
![]()
The derivative of the function y = x3 is
The derivative evaluated at x = 1 is 3, so the equation of the tangent line is
Support this result by graphing y = x3 and y = 3(x - 1) + 1 in a [-3, 3, 1] x [-5, 5, 1] viewing window.

The line appears to be tangent to the curve at x = 1, which provides graphical support that the equation of the tangent line is correct.
Other Derivative Rules
Many derivatives are found by using more than one rule. The rules for finding the derivative of a constant multiple of a function and the sum and difference of two functions can be used to find the derivatives of polynomials. The derivative of the polynomial found by using the rules can then be supported graphically.
The Derivative of a Constant Function Rule
If f is the function with the constant value c, then
The Constant Multiple Rule
The Constant Multiple Rule says: If f is a differentiable function of x and c is a constant then
The Sum and Difference Rule
The Sum and Difference Rule says: If f and g are differentiable functions of x, then
Derivative of a Polynomial
The previous two rules, along with the Power Rule, can be used to find the derivative of any polynomial. For example, the derivative of y = x4 - 2x3 + 5x2 - 7x + 11 is y' = 4x3 - 6x2 + 10x - 7 . Graphs can provide support for the result.
-
Enter the following in the Y= editor:
Y1 = X^4 - 2X^3 + 5X^2 - 7X + 11
Y2 = nDeriv(Y1,X,X)
Y3 = 4X^3 - 6X^2 + 10X - 7
- Unselect Y1.

- Display the graphs of Y2 and Y3 in a [-3, 3, 1] x [-25, 25, 5] window.
- Use the Trace feature and the up and down arrow keys to confirm that the graphs of Y2 and Y3 appear to be the same.
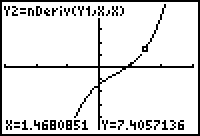

Both graphs appear to be the same, which is graphical support that the derivative defined in Y3 is correct.
The Product Rule
What is the derivative of the product of two differentiable functions? In other words, if u and v are differentiable functions of x then what is the derivative of their product,
![]() ?
?
After using the Sum and Difference Rule you might think there is a similar rule for the derivative of a product. However, you can illustrate that this is not the case by displaying a counterexample with your calculator.
A Counterexample
Show that
![]()
-
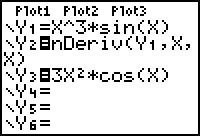
Enter the following:
Y1 = X^3*sin(X)
Y2 = nDeriv(Y1,X,X)
Y3 = 3X2 *cos(X)
- Unselect Y1.
- Display the graphs in a [-3, 3, 1] x [-25, 25, 5] window.
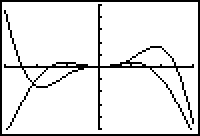
The two graphs are not the same, which is graphical evidence that
![]() .
.
The Product Rule for derivatives actually says:
![]()
Using this rule to find the derivative of y = x3 sin x gives
Provide graphical support for this derivative.
- Change Y3 to X^3 * cos(X) + 3X^2 *sin(X)

- Display the graphs in a [-3, 3, 1] x [-25, 25, 5] window.
- Use Trace and the up and down arrow keys to see if Y2 and Y3 are the same.


Tracing on both graphs produces the same coordinates. This is graphical support that the derivative defined in Y3 is correct.
The Quotient Rule
The Quotient Rule for derivatives says: If u and v are differentiable functions of x then
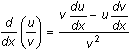
12.2.1 Use the Quotient Rule to find the derivative of
![]() . Support your result graphically. Click here for the answer.
. Support your result graphically. Click here for the answer.