When y = sin x is increasing the derivative is positive. When y = sin x is decreasing the derivative is negative.
When y = sin x has a turning point the derivative is zero.
The derivative of y = sin x is y = cos x.
The derivative of y = sin 3x is the function y = 3cos 3x. We usually write y ' = 3 cos 3x.
The derivative of y = sin 4x is y ' = 4cos 4x.
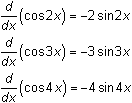

The derivative is
![]() .
.
Graphical support:

|
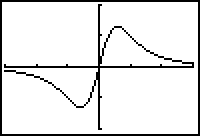
|
| [-3, 3, 1] x [-2, 2,1] |
False. A calculator can only be used to support, not prove analytic work.
False
![]()
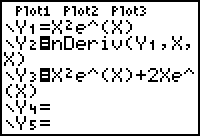
|
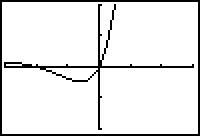
|
| [-3, 3, 1] x [-2, 2, 1] |
![]()

[-3, 3, 1] x [-5, 5, 1]
©Copyright 2007 All rights reserved. | Trademarks | Privacy Policy | Link Policy