In this lesson you will use the TI-83 Numeric Derivative feature to graph derivatives of various functions. These graphs will provide clues for differentiation rules. Analytic confirmation of these rules can be found in most calculus books.

The Derivative of y = sin x

Graph the function y = sin x and its derivative. Examine the graph of the derivative and determine how it relates to the graph of the function. Notice the values of the derivative when the function is increasing and when it is decreasing.

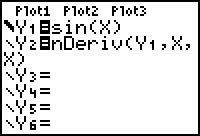
• Make sure your calculator is in radian mode. Enter Y₁ = sin(X) and Y₂ = nDeriv(Y₁,X,X).
• Change the graphing style of Y₁ to "thick."

• Display both graphs in a viewing window.

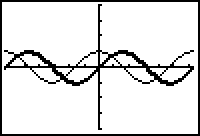
12.1.1 When the graph of y = sin x is increasing, what is true about its derivative? When the graph of y = sin x is decreasing, what is true about its derivative? Click here for the answer.

12.1.2 What is the value of the derivative when y = sin x has a turning point? Click here for the answer.

12.1.3 Make a conjecture about what function the derivative of y = sin x might be. Enter the function you conjectured into Y₃ and determine if the graphs defined in Y₂ and Y₃ coincide. Click here for the answer.

You should consult a calculus book for an analytic determination of the derivative of y = sin x to confirm your conjecture.

The Derivative of y = cos x

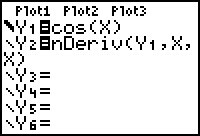
Graph y = cos x and its derivative in the same viewing window.

• Change Y₁ to cos(X). Keep the "thick" graphing style.

• Display both graphs in a viewing window.

12.1.4 Make a conjecture about the derivative of y = cos x. Provide graphical support for your conjecture by graphing your function in Y₃ to see if it produces the same graph as the derivative. Click here for the answer.

Consult a calculus book to confirm your conjecture about the derivative of y = cos x.

The procedure used above may be extended to include more general forms of familiar functions.

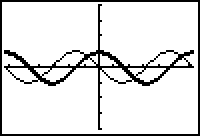
The Derivative of y = sin kx

Determine the form of the derivative of y = sin kx by exploring the form with different values of k. First explore the derivative of y = sin 2x.

• Enter Y₁ = sin(2X) and Y₂ = nDeriv(Y₁,X,X)
• Set the graphing style of Y₁ to "thick."

• Display both graphs in a viewing window.

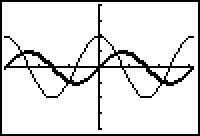
12.1.5 What is the amplitude of the derivative? What is the period of the derivative? Click here for the answer.

12.1.6 Write an equation for the derivative of y = sin 2x. Provide graphical support for your answer by graphing your equation in Y₃, which should match the graph of Y₂. Click here for the answer.

12.1.7 Graph y = sin 3x and its numeric derivative. Make a conjecture about the function that represents the derivative. Graph your conjecture together with the numeric derivative. Are they the same?

Repeat this process for y = sin 4x. Click here for the answers.

12.1.8 What do you think the derivative of y = sin kx, where k is a constant, might be? Click here for the answer.

The Derivative of y = cos kx

12.1.9 Use the previous graphical procedures to make and support conjectures for the derivatives of the following:

y = cos 2x

y = cos 3x

y = cos 4x

Click here for the answers.

12.1.10 Based on your previous answers, what is the derivative of y = cos(kx), if k is a constant? Click here for the answer.

The Derivative of y = e^x

Another derivative that is easily found by graphing is that of y = e^x.

• Enter Y₁ = e^(X) and Y₂ = nDeriv(Y₁,X,X)
  e^( is the "2^nd" feature above .
• Make the graphing style of Y₁ "thick."

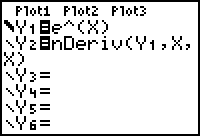
• Display both graphs in a [-3, 3, 1] x [-5, 5, 1] window.

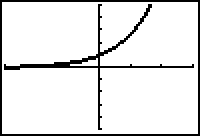
There appears to be only one graph.

12.1.11 Use the Trace feature and the arrow keys to move to various points on the graphs and jump back and forth between Y₁ and Y₂ by using the up and down arrow keys. What do you discover? Click here for the answer.

Using a Table of Values Another way to support the answer to the last question is to use the Table feature to make a table of values for Y1 and Y2. This allows you to compare values of Y1 and Y2 for selected values of x.

12.1.12 Use your discovery to make a conjecture about the derivative of y = e^x. Click here for the answer.

The Derivative of y = e^kx

Sometimes it is hard to decide if two functions are equal by looking at their graphs. It helps to compare their values using tables.

12.1.13 Use Tables and the graphical methods of this lesson to discover the derivatives of the following functions:

y = e^2x

y = e^3x

y = e^4x

Click here for the answer.

12.1.14 Based on your results, what is the derivative of y = e^kx? Click here for the answer.

The Chain Rule

There is a pattern in many of the derivatives of this lesson.

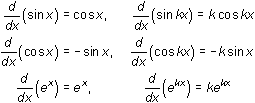
12.1.15 Based on these derivatives, what might be the derivative of y = f(kx), where k is a constant and f is an unknown function? Click here for the answer.

The answer to the previous question is a special case of a theorem called the The Chain Rule for Derivatives. Find this rule in a calculus book and see how it applies to this lesson.