In this lesson you will use several different features of the TI-83 to find and understand derivatives.

In Module 9 you saw that velocities correspond to slopes in the graph of position vs time. Average velocity corresponds to the slope of a

A secant line is a line through two points on a curve.

secant line that connects two points, and instantaneous velocity corresponds to the slope of a line tangent to the curve.

Average velocity is given by , which is the slope of a secant line through the points
(a, f(a)) and (a+h, f(a+h)).

Instantaneous velocity is given by , which is the slope of the tangent line to the curve at (a, f(a)).

The slope of the tangent line to the graph of a function at a point is called the derivative of the function at that point. The formal definition of derivative is given below.

Formal Definition of Derivative

The derivative of a function f at x = a is

provided the limit exists.

Illustrating Secant Line Convergence

For functions that have a tangent line, if the point (a, f(a)) on the curve is fixed, as h approaches zero the second point (a+h, f(a+h)) approaches the fixed point and the corresponding secant lines converge to the tangent line at that point.

The procedure outlined below will find the value of the derivative of the function f(x) = 2x - x² at the point (0.5, 0.75) using a method similar to the one you used to find instantaneous velocities.

1. Find the slopes of several secant lines and use them to estimate the slope of the tangent line at x = 0.5.
2. Then take the limit of the slopes of the secant lines to find the derivative.

The graph below illustrates f(x) = 2x - x² in a [-1, 3, 1] x [-1, 2, 1] window, with three secant lines through the fixed point (0.5, 0.75) that approximate the tangent line at (0.5, 0.75).

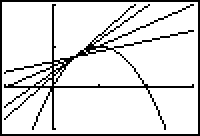
Finding Slopes of Secant Lines

The first step in the procedure outlined above is to find the slopes of secant lines that will be used to estimate the derivative. To find the slopes you need to enter the function f(x) = 2x - x² in the Y= editor.

• Define Y₁ = 2X - X²

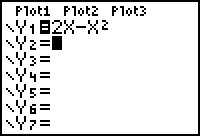
The slope of the secant line through the points (0.5, f(0.5)) and (0.5 + h, f(0.5 + h)) can be found by evaluating the difference quotient

.

We are interested in values of h that are small so that the two points are close together. The resulting secant line will approximate the tangent line.

You may evaluate the difference quotient for h = 0.1 on the TI-83 by using a two-part command. The first part of the command will store 0.1 in h and the second part of the command will evaluate the difference quotient. The two commands will be combined together with the colon symbol.

• Store 0.1 in H by pressing [H]. "H" is above in the last column.
  Don't press yet because another command will be combined with this command.
• Combine the next command by pressing [:]. ":" is above the key on the bottom row.
• Enter the difference quotient: (Y₁(0.5+H) - Y₁(0.5)) / H.
• Execute both commands by pressing .

The slope of the secant line containing (0.5, f(0.5)) and (0.6, f(0.6)) is 0.9.

Using Smaller Values of h

As the point (0.5 + h, f(0.5 + h)) approaches the point (0.5, f(0.5)), h approaches 0 and the secant lines converge to the tangent line.

To evaluate the difference quotient for smaller values of h, change the value of H in the last expression on the Home screen from 0.1 to 0.01 and evaluate the difference quotient.

• Recall the last expression by pressing [ENTRY].
• Move the cursor to the "1" in the expression 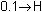  by using the arrow keys.
• Change to insert mode by pressing [INS].
• Insert a zero by pressing .
• Evaluate the difference quotient with the new value of H by pressing .

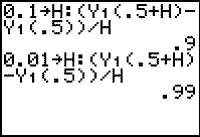
The slope of the corresponding secant line is 0.99.

• Evaluate the difference quotient with h = 0.001 and with h = 0.0001.

The slopes of the secant lines are 0.999 and 0.9999, respectively.

10.1.1 Predict the derivative at (0.5, f(0.5)). Click here for the answer.

Left-hand Difference Quotients

In the procedure above, right-hand difference quotients were used. Left-hand difference quotients may be found by letting h be a negative number.

• Evaluate the difference quotient with h = -0.01 and h = -0.001.
  Insert a negative sign and then use to delete zeros in the previous expression.

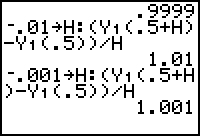
The slopes of the corresponding secant lines are 1.01 and 1.001. With the fixed point (0.5, 0.75), one secant line passes through (0.49, f(0.49)) and the other through (0.499, f(0.499)).

Finding a Derivative at a Point

As stated earlier, the derivative at x = 0.5 is defined to be the limit

.

Before this limit can be evaluated, the expression must be expanded and simplified. Recall that the function of interest is f(x) = 2x - x².

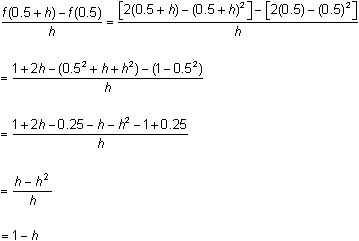
Therefore, and the derivative of f(x) = 2x - x² at x = 0.5 is 1.

Using the Numeric Derivative Command

You can also approximate the derivative of the function at a point by using the numeric derivative command nDeriv(, which is found in the Math menu. The syntax for finding a derivative at a point is nDeriv(expression,variable,value).

• Go to the Home screen by pressing [QUIT].
• Open the Math menu by pressing . nDeriv( is the eighth item in the menu.

• Paste nDeriv( to the Home screen by pressing .
• Complete the command nDeriv(Y₁,X,0.5).
• Execute the command by pressing .

The nDeriv Command nDeriv( actually evaluates a symmetric difference quotient and approximates the derivative. You can add an optional fourth parameter to change the default value of h, which is set at 0.001. For example, to evaluate the symmetric difference quotient at x=0.5 with h = 0.01 enter the command nDeriv(Y1,X, 0.5, 0.01)

Drawing the Tangent Line

Because the point on the curve and the derivative at that point are both known, an equation for the tangent line may be found by using the

An equation for the line through the point (x1, y1) with slope m is y - y1 = m(x - x1).

point-slope form of a line. If the slope of the tangent line at (0.5, 0.75) is 1, then an equation for the tangent line is y - 0.75 = 1·(x - 0.5).

Graph f(x) = 2x - x² and its tangent line at (0.5, 0.75).

• Set Y₁ = 2X - X².
• Set Y₂ = (X-0.5) + 0.75.
• Graph both the function and the tangent line in a [-1, 3, 1] x [-1, 2, 1] window.

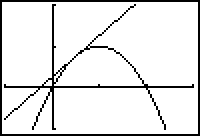
The line appears to be tangent to the curve at x = 0.5.