In this lesson you will modify a piecewise function to make it continuous and then graph the function using Boolean operators.

Consider the function defined by

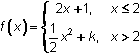
8.3.1 By using the definition of continuity, find the value of k that makes the function continuous at
x = 2. Click here for the answer.

Graphing a Piecewise Function

Display the graph of 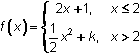using the value of k that makes the function continuous.

• Set Xres = 1.
• Enter
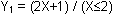
  You can paste "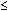 " from the Test menu by pressing [TEST] . [TEST] is above .
• Enter Y₂ = ( (1/2)X²+3 ) / (X>2)
  The symbol ">" is in the TEST menu.
• Graph the function in a [-3, 7, 1] x [-3, 25, 5] window.

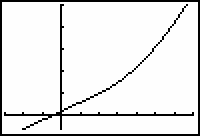
The graph appears to be continuous at x = 2.

8.3.2 Describe how the graph would change if you changed k to 7. Click here for the answer.

Illustrate the result of changing the value of k to 7.

• Set Y₂=( (1/2)X²+7 ) / (X>2).

Editing Existing Expressions Rather than retyping the entire expression in Y2 you can simply replace the "3" with a "7". Move the cursor on to the "3" and press . The old value should be replaced since the calculator is in the overwrite mode. The calculator shows it is in the overwrite mode when the cursor is a blinking solid rectangle. It can be changed from overwrite to insert mode and back again by pressing [INS]. ([INS] is above in the first row of keys.) Each time you press [INS] the mode changes, or "toggles," between overwrite and insert. In insert mode, the cursor is a blinking underline character. Whenever an arrow key or is pressed, the calculator returns to overwrite mode.

• Display the graph of the function by pressing .

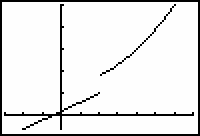
The second part of the piecewise function has been shifted upward, and the function is no longer continuous at x = 2. The discontinuity in this modified function (k = 7) is a jump discontinuity.

8.3.3 Evaluate the left- and right-hand limits of the piecewise function with k = 7 at x = 2. Click here for the answer.