The discontinuity you investigated in Lesson 8.1 is called a removable discontinuity because it can be removed by redefining the function to fill a hole in the graph. In this lesson you will examine three other types of discontinuities: jump, oscillating, and infinite.

A Jump Discontinuity

The function has a jump discontinuity at x = 0. Graphing the function can illustrate the reason for the name of this type of discontinuity.

• Set Xres = 1.
• Enter the expression Y₁ = abs(X)/X in the Y= Editor.
  The "abs(" function can be pasted from the catalog by pressing [CATALOG] .

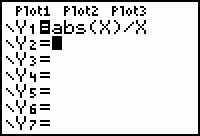
• Graph the function in a ZDecimal window.

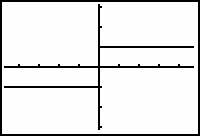
The function is not continuous at x = 0 because x = 0 is not in the domain of the function.

The function is said to have a jump discontinuity because it jumps from y = -1 to y = 1 at x = 0. The left- and right-hand limits are defined as x approaches 0, but is undefined because

For any jump discontinuity, the one-sided limits are unequal.

An Oscillating Discontinuity

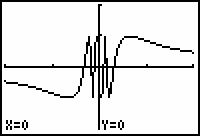
The function has a discontinuity at x = 0 because it is not defined at x = 0. This discontinuity is called an oscillating discontinuity. The oscillating discontinuity can be illustrated by viewing its graph in several windows that increasingly zoom in around the y-axis.

• Graph 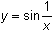in a [-2, 2, 1] x [-2, 2, 1] window.

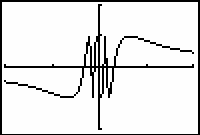
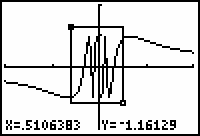
It is hard to tell what is happening near x = 0 by looking at the graph. You can magnify a portion of the graph near x = 0 by using a feature in the Zoom menu called ZBox (Zoom Box).

• Display the Zoom menu by pressing .

• Select the Zoom Box (1:ZBox) feature by pressing .

This feature will allow you to magnify the region around the y-axis by drawing a box around the part of the window you want to magnify.

• Move the cursor to the upper left corner of the desired box by using the arrow keys.

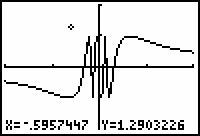
• Mark the upper left corner by pressing .
• Move the cursor to the diagonally opposite corner by using the arrow keys.

You should see the outline of a box evolve as you move the cursor.

• Finish identifying the box by pressing

The region inside the box is magnified to fill the entire viewing screen.

The Zoom Box feature magnifies the graph by adjusting the Window values to match the box corner coordinates.

This window shows even more oscillations than the previous one.

• Use the Zoom Box feature to zoom in further around the y-axis.

 

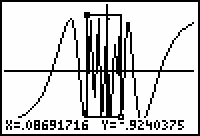
No matter how many times you zoom in, the graph will continue to oscillate between y = 1 and y = -1. In fact, there are infinitely many oscillations packed near x = 0. That is why is said to have an oscillating discontinuity at x = 0. The left- and right-hand limits do not exist in this case.

ZBox Feature The first corner that you mark when you use zoom box can be any one of the four corners, not just the upper left corner as in the example above. The only requirement is that the second corner be diagonally opposite the first.

An Infinite Discontinuity

The function y = tan(x) has a third type of discontinuity at . This discontinuity is called an infinite discontinuity.

• Graph y = tan(x) in a 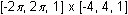window.

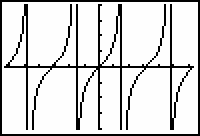
8.2.1 Based on the graph, why do you think y = tan(x) is said to have an infinite discontinuity at ?

Click here for the answer.