Page 59 - Activités algorithmiques avec Python en spécialité Mathématiques

Thème : simulation & espérances
TI-83 Premium CE Édition Python TI-Nspire CX II-T
Niveau : spécialité maths Terminale
L'approximation « Monte Carlo »
L. DIDIER & R. CABANE
Fiche méthode
Objectif 1 : proposition de résolution
Stratégie
On crée deux fonctions dans ce script :
▸ Une « fonction de décision » d qui prend comme arguments deux réels x et y et qui renvoie le nombre réel correspondant au carré de la distance OM entre O(0,0) et M(x,y) diminué de 1 (l’usage de la racine carrée n’est ici pas utile et consomme du temps de calcul) ; on teste si d(a,b) est négatif pour savoir si on est dans la zone souhaitée.
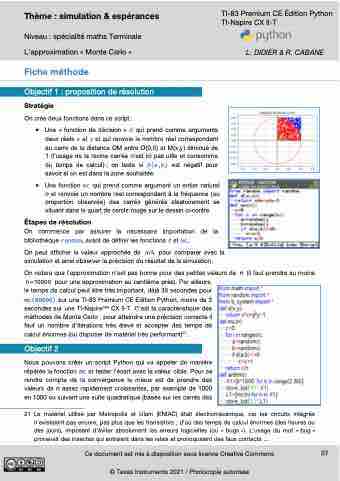
▸ Une fonction mc qui prend comme argument un entier naturel n et renvoie un nombre réel correspondant à la fréquence (ou proportion observée) des carrés générés aléatoirement se situant dans le quart de cercle rouge sur le dessin ci-contre.
Étapes de résolution
On commence par assurer la nécessaire importation de la bibliothèque random, avant de définir les fonctions d et mc.
On peut afficher la valeur approchée de π/4 pour comparer avec la simulation et ainsi observer la précision du résultat de la simulation.
On notera que l’approximation n’est pas bonne pour des petites valeurs de n (il faut prendre au moins n=10000 pour une approximation au centième près). Par ailleurs,
le temps de calcul peut être très important, déjà 35 secondes pour mc(80000) sur une TI-83 Premium CE Edition Python, moins de 3 secondes sur une TI-NspireTM CX II-T. C’est la caractéristique des méthodes de Monte Carlo : pour atteindre une précision correcte il faut un nombre d’itérations très élevé et accepter des temps de
21 calculénormes(oudisposerdematérieltrèsperformant) .
Objectif 2
Nous pouvons créer un script Python qui va appeler de manière répétée la fonction mc et tester l’écart avec la valeur cible. Pour se rendre compte de la convergence le mieux est de prendre des valeurs de n assez rapidement croissantes, par exemple de 1000 en 1000 ou suivant une suite quadratique (basée sur les carrés des
21 Le matériel utilisé par Metropolis et Ulam (ENIAC) était électromécanique, car les circuits intégrés n’existaient pas encore, pas plus que les transistors ; d’où des temps de calcul énormes (des heures ou des jours), imposant d’éviter absolument les erreurs logicielles (ou « bugs »). L’usage du mot « bug » provenait des insectes qui entraient dans les relais et provoquaient des faux contacts ...
Ce document est mis à disposition sous licence Creative Commons 57 © Texas Instruments 2021 / Photocopie autorisée