Page 58 - Activités algorithmiques avec Python en spécialité Mathématiques

Thème : simulation & espérances
TI-83 Premium CE Édition Python TI-Nspire CX II-T
Niveau : spécialité maths Terminale
L'approximation « Monte Carlo »
L. DIDIER & R. CABANE
disque, et les carrés « bleus » qui ne sont pas de ce type. On admet aisément que le total des aires des carrés rouges est proche (et supérieur) à l’aire du quart de disque grisé (et d’autant plus proche que M est grand), de sorte que la proportion des carrés rouges parmi l’ensemble des petits carrés (notons-la p ) est une approximation de π/4 (d’autant meilleure que M est grand).
Or, approcher des proportions au moyen d’expériences aléatoires est exactement l’objectif de la Statistique. Nous procédons donc à un tirage aléatoire de petits carrés au sein du carré ABDG (avec une loi uniforme sur les M2 petits carrés) ; soit la variable aléatoire Z valant 1 si le petit carré tiré est rouge et 0 sinon. La probabilité d’avoir Z=1 est exactement p , et c’est aussi l’espérance de Z. Pour estimer p , on considère un grand nombre n de tirages indépendants, suivant la même loi que Z, de sorte que quand n tend vers l’infini, la proportion de carrés rouges obtenus converge vers l’espé- rance de Z, soit p . Le nombre π peut donc être approché par 4 fois la proportion de carrés rouges.
Pour tirer un petit carré au hasard, il suffit de tirer l’abscisse et l’ordonnée de son coin en bas à gauche ; pour cela, on trouve dans le module random une fonction random qui réalise ce dont nous avons besoin.
En effet, cette fonction tire une valeur au hasard parmi M=253 valeurs régulièrement réparties entre 0 et 1 : c’est bien un très grand nombre (valant environ 1016 ).
Objectifs
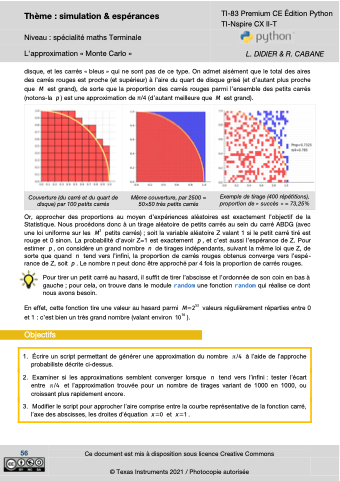
Couverture (du carré et du quart de disque) par 100 petits carrés
Même couverture, par 2500 = 50×50 très petits carrés
Exemple de tirage (400 répétitions), proportion de « succès » = 73,25%
1. Écrire un script permettant de générer une approximation du nombre π/4 à l’aide de l’approche probabiliste décrite ci-dessus.
2. Examiner si les approximations semblent converger lorsque n tend vers l’infini : tester l’écart entre π/4 et l’approximation trouvée pour un nombre de tirages variant de 1000 en 1000, ou croissant plus rapidement encore.
3. Modifierlescriptpourapprocherl’airecompriseentrelacourbereprésentativedelafonctioncarré, l’axe des abscisses, les droites d’équation x=0 et x=1 .
56
Ce document est mis à disposition sous licence Creative Commons
© Texas Instruments 2021 / Photocopie autorisée