Page 55 - Activités algorithmiques avec Python en spécialité Mathématiques

Thème : loi binomiale
TI-83 Premium CE Édition Python TI-82 Advanced Édition Python
Niveau : spécialité maths Terminale
Un problème de surréservation
L. DIDIER & R. CABANE
Une réponse probabiliste est aussi envisageable ; elle consisterait à faire un calcul d’espérance mathé- matique, et ajuster n de sorte que l’espérance de Gn soit maximale, mais c’est assez compliqué.
Une réponse algorithmique consiste à simuler la situation suffisamment de fois pour que la moyenne des valeurs simulées de Gn se stabilise autour de l’espérance de Gn (loi des grands nombres), avant d’ajuster n pareillement.
Nspire CX Le nombre de calculs requis est assez élevé, néces- sitant une bonne puissance de calcul ; c’est une situation où une
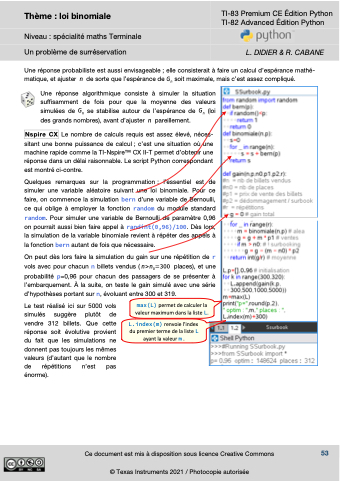
machine rapide comme la TI-NspireTM CX II-T permet d’obtenir une réponse dans un délai raisonnable. Le script Python correspondant est montré ci-contre.
Quelques remarques sur la programmation : l’essentiel est de simuler une variable aléatoire suivant une loi binomiale. Pour ce faire, on commence la simulation bern d’une variable de Bernoulli, ce qui oblige à employer la fonction random du module standard random. Pour simuler une variable de Bernoulli de paramètre 0,96 on pourrait aussi bien faire appel à randint(0,96)/100. Dès lors, la simulation de la variable binomiale revient à répéter des appels à la fonction bern autant de fois que nécessaire.
On peut dès lors faire la simulation du gain sur une répétition de r
vols avec pour chacun n billets vendus ( n>n0=300 places), et une
probabilité p=0,96 pour chacun des passagers de se présenter à l’embarquement. À la suite, on teste le gain simulé avec une série d’hypothèses portant sur n, évoluant entre 300 et 319.
Le test réalisé ici sur 5000 vols simulés suggère plutôt de vendre 312 billets. Que cette réponse soit évolutive provient du fait que les simulations ne donnent pas toujours les mêmes valeurs (d’autant que le nombre de répétitions n’est pas énorme).
max(L) permet de calculer la valeur maximum dans la liste L.
L.index(m) renvoie l’index du premier terme de la liste L ayant la valeur m .
Ce document est mis à disposition sous licence Creative Commons 53 © Texas Instruments 2021 / Photocopie autorisée