Page 24 - Activités algorithmiques avec Python en spécialité Mathématiques

Thème : probabilités
TI-83 Premium CE Edition Python TI-Nspire CX II-T
Niveau : spécialité maths Première + Terminale
Marches aléatoires
L. DIDIER & R. CABANE
Fiche méthode
Marche aléatoire 1D
▶ Objectif 1 :
Pour simuler la variable aléatoire Y, on peut se servir de la fonction randint fournie par la bibliothèque (ou module) random, nécessitant deux paramètres pour préciser l’intervalle d’entiers entre lesquels les nombres au hasard seront fournis. Voir l’appendice 1 pour plus de détails.
Ici, on attend des nombres 0 ou 1 (probabilité 1⁄2) ; pour obtenir des nombres -1 ou 1, une transforma- tion arithmétique suffit alors (2*randint(0,1)-1). L’espérance est évidemment nulle.
Une autre fonction fournie par ce module est choice, qui prend en paramètre la liste des valeurs entre lesquelles un tirage au hasard (équiprobable) est recherché. C’est le mécanisme du « pile ou face ».
Une représentation très simple de la marche aléatoire peut être obtenue en mode texte, en faisant défiler des lignes où une étoile est placée comme le pion. Pour positionner le caractère * dans la ligne, on le fait précéder d’un nombre variable d’espaces (c’est le rôle de la variable k).
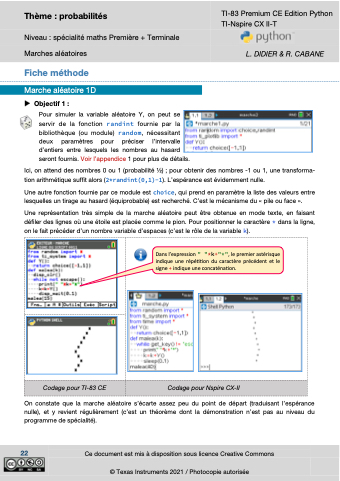
Dans l’expression " "*k+"*", le premier astérisque indique une répétition du caractère précédent et le signe + indique une concaténation.
On constate que la marche aléatoire s’écarte assez peu du point de départ (traduisant l’espérance nulle), et y revient régulièrement (c’est un théorème dont la démonstration n’est pas au niveau du programme de spécialité).
Codage pour TI-83 CE
Codage pour Nspire CX-II
22
Ce document est mis à disposition sous licence Creative Commons
© Texas Instruments 2021 / Photocopie autorisée