Pode efetuar cálculos estatísticos para analisar dados. O exemplo seguinte ajusta um modelo de regressão linear y=mx+b às duas listas nas colunas A e B.

1.

No menu Estatística, selecione Cálculo estatístico > Regressão linear (mx+b) para escolher o modelo de regressão.

Surge a caixa de diálogo Regressão linear (mx+b).

2.

Introduza a[] como a coluna para a Lista X.

3.

Introduza b[] como a coluna para a Lista Y.

4.

Para guardar a equação de regressão numa variável específica, substitua Guardar RegEqn em pelo nome da variável.

5.

Introduza c[] como a coluna para o 1º Resultado.

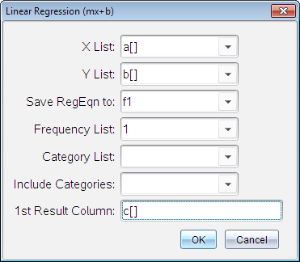
6.

Clique em OK.

A aplicação Listas e Folha de cálculo insere duas colunas: uma com os nomes dos resultados e outra com os valores correspondentes.

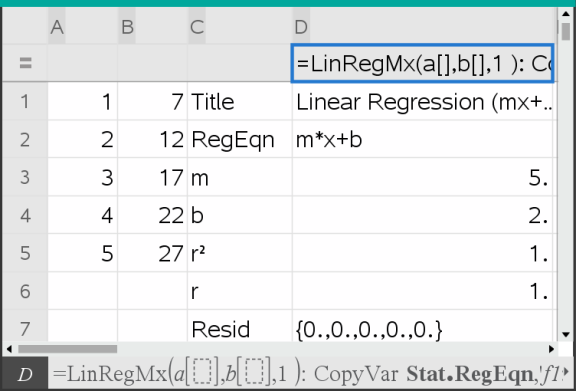
Nota: Os resultados estão ligados aos dados de origem. Por exemplo, se mudar um valor da coluna A, a equação de regressão é atualizada automaticamente.

 

A aplicação Listas e Folha de cálculo guarda resultados estatísticos com o nome de um grupo de variáveis com o formato stat.nnn, em que nnn corresponde ao nome do resultado (por exemplo, stat.RegEqn e stat.Resid). A utilização de nomes padrão para as variáveis torna mais fácil identificar e utilizar as variáveis estatísticas mais tarde. Se quiser utilizar um grupo de variáveis personalizadas em vez do nome padrão, pode editar a fórmula na célula da fórmula da coluna.

Pode utilizar a seguinte fórmula para guardar os resultados no grupo de variáveis MystatsB.

=LinRegMx(a[],b[],1 ): CopyVar Stat., MystatsB.

Posteriormente, pode ver os resultados, introduzindo a seguinte expressão na aplicação Calculadora ou noutra coluna da aplicação Listas e Folha de cálculo:

Resultados MystatsB.

 

O menu Cálculos estatísticos permite selecionar a partir dos cálculos descritos abaixo Para obter mais informações, consulte o Guia de Referência -do  TI Nspire™.

Estatística de uma variável (OneVar)

Analisa dados com uma variável medida. Pode especificar uma lista de frequências opcionais. Os dados estatísticos devolvidos com esta técnica de análise são:

•

Média da amostra, x

•

Soma dos dados, Gx

•

Soma dos quadrados dos dados, Gx2

•

Desvio padrão da amostra, sx

•

Desvio padrão da população, sx

•

tamanho da amostra, n

•

X-mín

•

primeiro quartil, Q1

•

Mediana

•

terceiro quartil, Q3

•

X-máx

•

Soma dos quadrados dos desvios, SSx = G(x Nx)2

Estatística de duas variáveis (TwoVar)

Analisa dados emparelhados. Lista 1 é a variável independente. Lista 2 é a variável dependente. Pode especificar uma lista de frequências opcionais. Os dados estatísticos devolvidos com esta técnica de análise são:

Para cada lista:

•

Média da amostra, x ou y

•

Soma dos dados, Gx ou Gy

•

Soma dos quadrados dos dados, Gx2 ou Gy2

•

Desvio padrão da amostra, sx = sn-1x ou sy = sn-1y

•

desvio padrão da população, sx = snx ou sy = sny

•

X-mín ou Y-mín

•

primeiro quartil, Q1X ou Q1Y

•

Mediana

•

terceiro quartil, Q3X ou Q3Y

•

X-máx ou Y-máx

•

Soma dos quadrados dos desvios, SSx = G(x Nx)2 ou SSy = G(y Ny)2

Dados adicionais:

•

Tamanho da amostra para cada conjunto de dados, n

•

Gxy

•

Coeficiente de correlação, R.

Linear Regression (mx+b) (LinRegMx) (Regressão linear)

Ajusta a equação do modelo y=ax+b aos dados com um ajuste de mínimos quadrados. Mostra os valores para m (declive) e b (y-interseção).

Linear Regression (a+bx) (LinRegBx) (Regressão linear)

Ajusta a equação do modelo y=a+bx aos dados com um ajuste de mínimos quadrados. Mostra os valores para a (y-interseção), b (declive), r2 e r.

Reta mediana-mediana (MedMed)

Ajusta a equação do modelo y=mx+b aos dados através da técnica da reta mediana-mediana (reta resistente), calculando os pontos do resumo x1, y1, x2, y2, x3 e y3. A reta-mediana mediana apresenta os valores para m (declive) e b (y-interseção).

Regressão quadrática (QuadReg)

Ajusta o polinómio de segundo grau y=ax2+bx+c aos dados. Mostra os valores para a, b, c e R2. Para três pontos de dados, a equação é um ajuste polinomial; para quatro ou mais, é uma regressão polinomial. São necessários pelo menos três pontos de dados.

Reegrssão cúbica (CubicReg)

Ajusta o polinómio de terceiro grau y=ax3+bx2+cx+d aos dados. Mostra os valores para a, b, c, d e R2. Para quatro pontos de dados, a equação é um ajuste polinomial; para cinco ou mais, é uma regressão polinomial. São necessários pelo menos quatro pontos.

regressão quártica, QuartReg

Ajusta o polinómio de quarto grau y=ax4+bx3+cx2+dx+e aos dados. Mostra os valores para a, b, c, d, e e R2. Para cinco pontos de dados, a equação é um ajuste polinomial; para seis ou mais, é uma regressão polinomial. São necessários pelo menos cinco pontos.

Regressão potencial (PowerReg)

Ajusta a equação do modelo y=axb aos dados com um ajuste de mínimos quadrados em valores transformados ln(x) e ln(y). Mostra os valores para a, b, r2 e r.

Regressão exponencial (ExpReg)

Ajusta a equação do modelo y=abx aos dados com um ajuste de mínimos quadrados em valores transformados x e ln(y). Mostra os valores para a, b, r2 e r.

Regressão logarítmica (LogReg)

Ajusta a equação do modelo y=a+b ln(x) aos dados com um ajuste de mínimos quadrados em valores transformados ln(x) e y. Mostra os valores para a, b, r2 e r.

Regressão sinusoidal (SinReg)

Ajusta a equação do modelo y=a sin(bx+c)+d aos dados com um ajuste de mínimos quadrados iterativo. Mostra os valores para a, b, c e d. São necessários pelo menos quatro pontos de dados São necessários pelo menos dois pontos por ciclo para evitar previsões de frequências falsas.

Nota: A saída da SinReg é sempre em radianos, independentemente da definição do modo Radianos/Graus.

Regressão logística (d=0) (Logistic)

Ajusta a equação do modelo y=c/(1+a*e-bx) aos dados com um ajuste de mínimos quadrados iterativo. Mostra valores para a, b e c.

Regressão logística (dƒ0) (LogisticD)

Ajusta a equação do modelo y=c(1+a*e(-bx))+d aos dados com um ajuste de mínimos quadrados iterativo. Mostra os valores para a, b, ce d.

Regressão linear múltipla (MultReg)

Calcula a regressão linear múltipla da lista Y nas listas X1, X2, …, X10.