Exemplo: Calcular uma distribuição para ajustar ao modelo de distribuição de Densidade de probabilidade normal.
| 1. | Clique na célula da fórmula da coluna (segunda célula a partir do topo) na coluna A. |
| 2. | Clique em Estatística > Distribuições > Densidade de probabilidade normal para selecionar o modelo de distribuição. |
A caixa de diálogo Distribuição de probabilidade Normal abre-se e mostra os campos para escrever ou seleccionar os argumentos para o cálculo.
| 3. | Prima Tab conforme necessário para se mover de campo para campo e fornecer cada argumento. Pode escrever os valores ou selecioná-los na lista pendente: |
| - | Valor X: Clique na seta pendente para selecionar qualquer lista no problema para fornecer os valores x para o cálculo. |
| - | Média: Escreva um valor para a média ou clique na seta pendente para seleccionar uma variável que contenha a média. |
| - | Desvio padrão: Escreva um valor para o desvio padrão ou selecione uma variável que contenha o desvio padrão. |
| 4. | Clique na caixa de verificação Desenhar para ver a distribuição representada graficamente em Dados e Estatística. |
Nota: A opção Desenhar não está disponível para todas as distribuições.
| 5. | Clique em OK. |
A aplicação Listas e Folha de Cálculo insere duas colunas: uma com os nomes dos resultados e uma com os valores correspondentes. Os resultados são representados graficamente em Dados e Estatística.
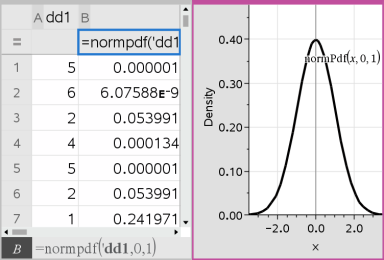
Nota: Os resultados estão ligados aos dados de origem. Por exemplo, pode alterar um valor na Coluna A e a equação atualiza-se automaticamente.
As distribuições seguintes estão disponíveis na aplicação Listas e Folha de Cálculo. Para obter mais informações relativas a estas funções, consulte o Guia de Referência do TI-Nspire™.
| • | Para devolver um resultado de distribuição baseado num valor, escreva a função numa célula. |
| • | Para devolver uma lista de resultados de distribuição baseada numa lista de valores, escreva a função numa célula da fórmula da coluna. Neste caso, especifique uma lista (coluna) que contenha os valores. Para cada valor na lista, a distribuição devolve um resultado correspondente. |
Nota: Para funções de distribuição que suporte a opção de desenho (normPDF, t PDF, χ² Pdf e F Pdf), a opção só está disponível se introduzir a função de distribuição numa célula de fórmula.
Densidade de probabilidade Normal (normPdf)
Calcula a função de densidade da probabilidade (pdf) para a distribuição normal num valor x especificado. As predefinições são a média μ=0 e o desvio padrão σ=1. A função de densidade de probabilidade (pdf) é:

Esta distribuição é utilizada para determinar a probabilidade da ocorrência de um determinado valor numa distribuição normal. A opção de desenho está disponível quando a Densidade de Probabilidade Normal é chamada a partir de uma célula de fórmula.
Quando aceder às distribuições a partir da célula de fórmula, tem de selecionar uma lista válida na lista pendente para evitar resultados imprevistos. Se aceder a partir de uma célula, tem de especificar um número para o valor x. A distribuição devolve a probabilidade de ocorrência do valor especificado.
Função cumulativa de distribuição Normal (normCdf)
Calcula a distribuição de probabilidade normal entre o Limite inferior e o Limite superior para a média especificada, μ (predefinição=0) e o desvio padrão, s (predefinição=1). Pode clicar na caixa de verificação Desenhar (Sombrear área) para sombrear a área entre os limites inferior e superior. As alterações ao Limite inferior e ao Limitesuperior iniciais atualizam automaticamente a distribuição.
Esta distribuição é útil para determinar a probabilidade de uma ocorrência de qualquer valor entre os limites inferior e superior na distribuição normal. É equivalente a calcular a área sob a curva normal especificada entre os limites.
Inverso da distribuição Normal (invNorm)
Calcula a função de distribuição normal cumulativa inversa para uma determinada área sob a curva de distribuição normal especificada pela média, μ, e pelo desvio padrão, s.
Esta distribuição é útil para determinar o valor x dos dados na área de 0 a x<1 quando o percentil é conhecido.
t Pdf (tPdf)
Calcula a função de densidade de probabilidade (pdf) para a distribuição-t com um valor x especificado. df (graus de liberdade) tem de ser > 0. A função de densidade de probabilidade (pdf) é:
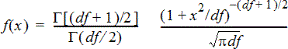
Esta distribuição é útil para determinar a probabilidade de uma ocorrência de um valor quando o desvio padrão da população não é conhecido e o tamanho da amostra é pequeno. A opção de desenho está disponível quando chamar t Pdf a partir de uma célula da fórmula.
t Cdf (tCdf)
Calcula a probabilidade de distribuição Student-t entre o Limite inferior e o Limite superior para o df (graus de liberdade) especificado. Pode clicar na caixa de verificação Desenhar (Sombrear área) para sombrear a área entre os limites. As alterações ao Limite inferior e ao Limite superior iniciais atualizam automaticamente a distribuição.
Esta distribuição é útil para determinar a probabilidade da ocorrência de um valor num intervalo definido pelos limites inferior e superior para uma população distribuída normalmente quando o desvio padrão da população não for conhecido.
t inverso (invt)
Calcula a função de distribuição de probabilidade-t cumulativa inversa especificada pelos Graus de liberdade, df, para uma determinada área sob a curva.
Esta distribuição é útil para determinar a probabilidade de uma ocorrência dos dados de 0 a x<1. Esta função é utilizada quando a média da população e/ou o desvio padrão da população não é conhecido.
c2 Pdf (c2 Pdf())
Calcula a função de densidade de probabilidade (pdf) para a distribuição c2 (chi ao quadrado) com um valor x especificado. df (graus de liberdade) tem de ser um número inteiro > 0. A função de densidade de probabilidade (pdf) é:
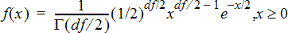
Esta distribuição é útil para determinar a probabilidade da ocorrência de um determinado valor a partir de uma população com uma distribuição c2 . A opção de desenho está disponível quando chamar c2 Pdf a partir de uma célula da fórmula.
c2 Cdf (c2 Cdf())
Calcula a distribuição de probabilidade c2 (chi quadrado) entre o Limite Inferior e o Limite Superior para o df (graus de liberdade) especificado. Pode clicar na caixa de verificação Desenhar (Sombrear área) para sombrear a área entre os limites inferior e superior. As alterações ao LimiteInferior e ao LimiteSuperior iniciais atualizam automaticamente a distribuição.
Esta distribuição é útil para determinar a probabilidade da ocorrência do valor em determinados limites de uma população com uma distribuição c2 .
F Pdf (F Pdf())
Calcula a função de densidade de probabilidade (pdf) para a distribuição F com um valor x especificado. numerador df (graus de liberdade) e denominador df têm de ser números inteiros > 0. A função de densidade de probabilidade (pdf) é:

|
em que |
n = graus de liberdade do numerador |
Esta distribuição é útil para determinar a probabilidade de duas amostras terem a mesma variância. A opção de desenho está disponível ao chamar F Pdf a partir de uma célula da fórmula.
F Cdf (F Cdf())
Calcula a probabilidade da distribuição F entre o LimiteInferior e o LimiteSuperior para o Numerdf (graus de liberdade) e Denomdf especificados. Pode clicar na caixa de verificação Desenhar (Sombrear área) para sombrear a área entre os limites inferior e superior. As alterações ao LimiteInferior e ao LimiteSuperior iniciais atualizam automaticamente a distribuição.
Esta distribuição é útil para determinar a probabilidade de uma observação individual ficar no intervalo entre o limite inferior e o limite superior.
Densidade de probabilidade Binomial (binomPdf())
Calcula uma probabilidade em x para a distribuição binomial discreta com o TentativasNum especificado e a probabilidade de sucesso (p) em cada tentativa. O parâmetro x pode ser um número inteiro ou uma lista de números inteiros. 0{p{1 tem de ser verdadeiro. TentativasNum tem de ser um número inteiro > 0. Se não especificar x, é devolvida uma lista de probabilidades de 0 a TentativasNum. A função de densidade de probabilidade (pdf) é:
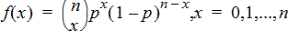
em que n = numtrials
Esta distribuição é útil para determinar a probabilidade de sucesso numa experiência de sucesso/insucesso na n-ésima prova Por exemplo, pode utilizar esta distribuição para determinar a probabilidade de tirar um certo número de face euro em cinco lançamentos de uma moeda.
Função cumulativa de distribuição Binomial (binomCdf())
Calcula uma probabilidade acumulada para a distribuição binomial discreta com o n número de tentativas e a probabilidade p de sucesso de cada tentativa.
Esta distribuição é útil para determinar a probabilidade de um sucesso numa experiência antes da conclusão de todas as experiências. Por exemplo, se sair face euro no lançamento de uma moeda for um sucesso e planear lançar a moeda 10 vezes ao ar, esta função dará a probabilidade de obter faces euro pelo menos uma vez em 10 lançamentos.
Binomial Inverso (invBinom())
Dado o número de tentativas (NumTrials) e a probabilidade de sucesso de cada tentativa (Prob), esta função devolve o número mínimo de sucessos, k, de forma a que a probabilidade cumulativa de k sucessos seja igual ou superior à probabilidade cumulativa dada (CumulativeProb).
Bionomial inverso relativamente a N (invBinomN())
Dada a probabilidade de sucesso de cada tentativa (Prob) e o número de sucessos (NumSuccess), esta função devolve o número mínimo de tentativas, N, de forma a que a probabilidade cumulativa de x sucessos é inferior ou igual à probabilidade cumulativa dada (CumulativeProb).
Densidade de probabilidade de Poisson (poissPdf())
Calcula uma probabilidade em x para a distribuição Poisson discreta com a média especificada, μ, que tem de ser um número real > 0. x pode ser um número inteiro ou uma lista de números inteiros. A função de densidade de probabilidade (pdf) é:
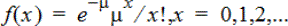
Esta distribuição é útil para determinar a probabilidade de obter um determinado número de sucessos antes do início de uma experiência. Por exemplo, pode utilizar este cálculo para prever o número de coroas que ocorreriam em 8 tentativas.
Função de distribuição Poisson (poissCdf())
Calcula a probabilidade acumulada para a distribuição Poisson discreta com a média especificada x.
Esta distribuição é útil para determinar a probabilidade que um determinado número de sucessos ocorram entre os limites superior e inferior de uma experiência. Por exemplo, pode utilizar este cálculo para prever o número de faces euro apresentadas entre o lançamento da moeda número 3 e o lançamento da moeda nº 8.
Função de densidade de probabilidade geométrica (geomPdf())
Calcula uma probabilidade em x, o número da tentativa em que ocorre o primeiro sucesso, para a distribuição geométrica discreta com a probabilidade de sucesso especificada p. 0{p{1 tem de ser verdadeiro. x pode ser um número inteiro ou uma lista de números inteiros. A função de densidade de probabilidade (pdf) é:

Esta distribuição é útil para determinar o número de tentativas mais provável antes de obter um sucesso. Por exemplo, pode utilizar este cálculo para prever quantos lançamentos de uma moeda são necessários para obter face euro.
Função de distribuição cumulativa geométrica (geomCdf())
Calcula uma probabilidade geométrica acumulada do LimiteInferior ao LimiteSuperior com uma probabilidade de sucesso especificada (p).
Esta distribuição é útil para determinar a probabilidade associada ao primeiro sucesso que ocorra durante as tentativas de 1 a n. Por exemplo, pode utilizar este cálculo para determinar a probabilidade que as faces euro apareçam no 1.º lançamento, 2.º lançamento, 3.º lançamento, ... n-ésimo lançamento