Du kan utføre statistiske beregninger for å analysere data. Følgende eksempel tilpasser en y=mx+b lineær regresjonsmodell til to lister i kolonnene A og B.

1.

Fra Statistikk-menyen, velg Stat beregning, og velg > Lineær regresjon (mx+b) for å velge regresjonsmodellen

Dialogboksen Lineær regresjon (mx+b) åpnes.

2.

Skriv a[] som kolonne for X-liste.

3.

Skriv b[] som kolonne for Y-liste.

4.

Hvis du vil lagre regresjonsligningen i en spesifisert variabel, erstatt Lagre RegLgn med navnet på variabelen.

5.

Skriv c[] som kolonne for 1. resultat.

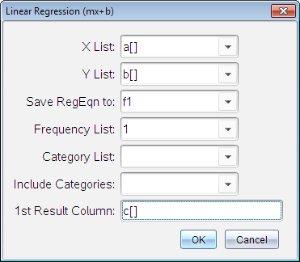
6.

Klikk på OK.

Lister & regneark setter inn to kolonner: en som inneholder navnene på resultatene, og en som inneholder de tilsvarende verdiene.

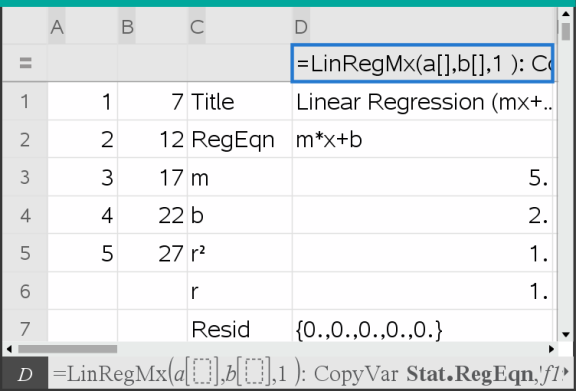
Merk: Resultatene er koblet til kildedataene. For eksempel kan du endre en verdi i kolonne A, og dermed oppdateres regresjonsligningen automatisk.

 

Lister & regnark lagrer statistiske resultater med bruk av et variabelgruppenavn med formatet stat.nnn, der nnn er resultatnavnet (f.eks. RegLig og stat.Rest). Ved å bruke standardnavn på variablene blir det enklere å identifisere og bruke statistikk-variablene senere. Du kan redigere formelen i kolonnens formelcelle hvis du vil bruke en egendefinert variabelgruppe istedenfor standardnavnet.

Du kan bruke følgende formel for å lagre resultatene i variabelgruppen MinestatsB.

=LinRegMx(a[],b[],1 ): KopiVar Stat., MinestatsB.

Senere kan du vise resultatene ved å legge inn følgende uttrykk i applikasjonen Kalkulator eller i en annen kolonne i Lister & regneark-applikasjonen:

MinestatsB.resultater

 

Stat beregninger-menyen lar deg velge fra beregningene som beskrevet nedenfor. For mer informasjon, se TI-Nspire™  referanseguide .

En-variabel-statistikk (EnVar)

Analyserer data med en målt variabel. Du kan spesifisere en valgfri frekvensliste. Statistiske data som returneres ved hjelp av denne analyseteknikken, er:

•

Utvalgsgjennomsnitt x,

•

Sum av dataene, Gx

•

Sum av kvadrerte data, Gx2

•

Utvalgets standardavvik, sx

•

Populasjonens standardavvik, sx

•

Utvalgsstørrelse, n

•

X-Min

•

Første kvartil, Q1

•

Median

•

Tredje kvartil, Q3

•

X-maks

•

sum av kvadratavvik, SSx = G(x Nx)2

Statistikk med to variabler (ToVar)

Analyserer parvise data. Liste 1 er den uavhengige variabelen. Liste 2 er den avhengige variabelen. Du kan spesifisere en valgfri frekvensliste. Statistiske data som returneres ved hjelp av denne analyseteknikken, er:

For hver liste:

•

Tilfeldig utvalg gjennomsnitt, x eller y

•

Summen av dataene, Gx eller Gy

•

Summen av kvadrerte data, Gx2 eller Gy2

•

Utvalgets standardavvik, sx = sn-1x eller sy = sn-1y

•

Populasjonens standardavvik, sx = snx eller sy = sny

•

X-min eller Y-min

•

Første kvartil, Q1X eller Q1Y

•

Median

•

Tredje kvartil, Q3X or Q3Y

•

X-maks eller Y-maks

•

Summen av kvadrerte avvik, SSx = G(x Nx)2 eller SSy = G(y Ny)2

Tilleggsdata:

•

Utvalgsstørrelse for hvert datasett, n

•

Gxy

•

Korrelasjonskoeffisient, R.

Lineær regresjon (mx+b) (LinRegMx)

Tilpasser modelligningen y=ax+b til dataene ved å bruke minste kvadraters metode. Den viser verdier for m (stigningstall) og b (y-skjæringspunkt).

Lineær regresjon (a+bx) (LinRegBx)

Tilpasser modelligningen y=a+bx til dataene ved å bruke minste kvadraters metode. Den viser verdiene fora (y-skjæringspunkt), b (stigningstall), rr2 og r.

Median-Median linje (MedMed)

Tilpasser modelligningen y=mx+b til datene ved å bruke median-median linjeteknikk (heltrukket linje) og beregner summen av punktene x1, y1, x2, y2, x3 og y3. Median-Median Linje viser verdiene for m (stigningstall) og b (y-skjæringspunkt).

Kvadratisk regresjon, KvadReg

Tilpasser annengrads polynom y=ax2+bx+c til datene. Den viser verdiene for a, b, c og R2. For tre datapunkter er ligningen en polynomisk tilpasning. For fire eller flere er den en polynomisk regresjon. Du trenger minst tre datapunkter.

Kubisk regresjon (KubReg)

Tilpasser tredjegrads polynom y=ax3+bx2+cx+d til dataene. Den viser verdier for a, b, c, d og R2. For fire datapunkter er ligningen en polynomisk tilpasning. For fem eller flere er den en polynomisk regresjon. Du trenger minst fire datapunkter.

fjerdegrads regresjon, QuartReg

Tilpasser fjerdegrads polynom y=ax4+bx3+cx2+dx+e til dataene. Den viser verdiene for for a, b, c, d, e og R2. For fem datapunkter er ligningen en polynomisk tilpasning. For seks eller flere er den en polynomisk regresjon. Du trenger minst fem datapunkter.

Potensregresjon (PowerReg)

Tilpasser modelligningen y=axb til dataene ved å bruke tilpasningen minste kvadraters metode og transformerte verdier ln(x) og ln(y). Den viser verdiene for a, b, r2, and r.

Eksponensiell regresjon (EkspReg)

Tilpasser modelligningen y=abx til dataene ved å bruke tilpasningen minste kvadraters metode og transformerte verdier x og ln(y). Den viser verdiene for a, b, r2, and r.

Logaritmisk regresjon (LogReg)

Tilpasser modelligningen y=a+b ln(x) til dataene ved å bruke tilpasningen minste kvadraters metode og transformerte verdier x og ln(y). Den viser verdiene for a, b, r2, og r.

Sinusregresjon (SinReg)

Tilpasser modelligningen y=a sin(bx+c)+d til dataene ved å bruke tilpasningen iterativ minste kvadraters metode. Den viser verdiene for a, b, c og d. Du trenger minst fire datapunkter. Du trenger minst to datapunkter pr. syklus for å unngå parallellberegnede frekvenser.

Merk: Utdata for SinReg er alltid i radianer, uavhengig av radian/gradmodus-innstilling.

Logistisk regresjon (d=0) (Logistisk)

Tilpasser modelligningen y=c/(1+a*e-bx) til datene med bruk av tilpasningen iterativ minste kvadraters metode. Den viser verdier for a, b, og c.

Logistisk regresjon (dƒ0) (LogisticD)

Tilpasser modelligningen y=c(1+a*e(-bx))+d til dataene med bruk av tilpasningen iterativ minste kvadraters metode. Den viser verdiene for a, b, c og d.

Multippel lineær regresjon (MultReg)

Beregner multiple lineære regresjoner av liste Y på lister X1, X2, …, X10.