Eksempel: Du kan beregne en fordeling for å tilpasse fordelingsmodellen Normal Pdf.
| 1. | Klikk på kolonnens formelcelle (andre celle fra toppen) i kolonne A. |
| 2. | Klikk på Statistikk > Fordelinger > Normal Pdf for å velge fordelingssmodellen. |
Dialogboksen for Normal Pdf åpnes og viser felter for inntasting eller valg av argumenter for beregningen.
| 3. | Trykk på Tab etter behov for å gå fra felt til felt og angi hvert argument. Du kan skrive inn verdier eller velge dem fra rullegardinlisten: |
| - | X-verdi: Klikk på rullegardinpilen for å velge en hvilken som helst liste i oppgaven, for å gi x-verdier for beregningen. |
| - | Gjennomsnitt: Tast inn en verdi for gjennomsnittet eller klikk på rullegardinpilen for å velge en variabel som inneholder gjennomsnittet. |
| - | Standardavvik: Tast en verdi for standardavvik, eller velg en variabel som inneholder standardavviket. |
| 4. | Klikk på avmerkingsboksen Tegn for å se fordelingen bli plottet i Data og statistikk. |
Merk: Tegne-alternativet er ikke tilgjengelig for alle fordelinger.
| 5. | Klikk på OK. |
Lister og regneark setter inn to kolonner: en som inneholder navnene på resultatene og en som inneholder de tilsvarende verdiene. Resultatene plottes i Data og statistikk.
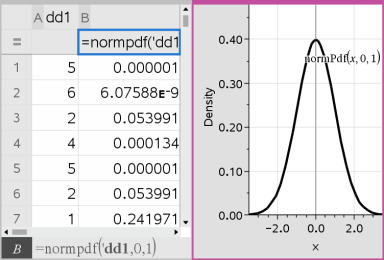
Merk: Resultatene er koblet til kildedataene. Du kan for eksempel endre en verdi i kolonne A, så oppdateres ligningen automatisk.
Følgende fordelinger er tilgjengelige fra applikasjonen Lister og regneark. For mer informasjon om disse funksjonene, se TI-Nspire™-referanseveiledningen.
| • | For å returnere et enkelt fordelingsresultat basert på en enkelt verdi, taster du funksjonen i en enkelt celle. |
| • | For å returnere en liste med fordelingsresultater basert på en liste med verdier, taster du funksjonen i en kolonnes formelcelle. I dette tilfellet spesifiserer du en liste (kolonne) som inneholder verdiene. For hver verdi i listen returnerer fordelingen et tilhørende resultat. |
Merk: For fordelingsfunksjoner som støtter tegne-alternativet (normPDF, t PDF, χ² Pdf og F Pdf), er alternativet kun tilgjengelig dersom du legger inn fordelingsfunksjonen i en formelcelle.
Normal Pdf (normPdf)
Beregner sannsynlighetstetthetsfunksjonen (pdf) for den normale fordelingen ved en spesifisert x-verdi. Standard er gjennomsnitt μ=0 og standardavvik σ=1. Funksjonen for sannsynlighetstetthet (pdf) er:

Denne fordelingen brukes til å bestemme sannsynligheten for forekomsten av en viss verdi i en normal fordeling. Tegne-alternativet er tilgjengelig når normal PDF aktiveres fra en formelcelle.
Når du åpner fordelinger fra formelcellen, må du velge en gyldig liste fra rullegardinmenyen for å unngå uventede resultater. Hvis du åpner fra en formelcelle, må du spesifisere et tall for x-verdien. Fordelingen returnerer sannsynligheten for at den verdien du spesifiserer, vil inntreffe.
Normal Cdf (normCdf)
Beregner den normale fordelingssannsynligheten mellom nedre grense og øvre grense for det spesifikke gjennomsnittet, μ (standard=0) og standardavviket, s (standard=1). Du kan klikke på Tegn (Skyggelegg område) i avmerkingsboksen for å skyggelegge området mellom nedre og øvre grense. Endringer som du foretar i opprinnelig nedre grense og øvre grense oppdaterer fordelingen automatisk.
Denne fordelingen er nyttig når du vil bestemme sannsynligheten for at en enkelt observasjon faller innenfor området mellom nedre og øvre grense i den normale fordelingen. Den er ekvivalent til å finne arealet under den spesifiserte normalkurven mellom grensene.
Invers Normal (invNorm)
Beregner den inverse, kumulative normale fordelingsfunksjonen for et gitt areal under den normale fordelingskurven som er spesifisert av gjennomsnitt μ og standardavvik s.
Denne fordelingen er nyttig når du vil bestemme x-verdien for data i arealet fra 0 to x<1 når persentilen er kjent.
t Pdf (tPdf)
Beregner funksjonen for sannsynlighetstetthet (pdf) for t-fordelingen ved en spesifisert x-verdi. df (frihetsgrader) må være > 0. Funksjonen for sannsynlighetstetthet (pdf) er:

Denne fordelingen er nyttig når du vil bestemme sannsynligheten for forekomsten av en verdi når populasjonens standardavvik ikke er kjent og utvalgets størrelse er liten. Tegne-alternativet er tilgjengelig når t Pdf aktiveres fra en formelcelle.
t Cdf (tCdf)
Beregner Student-t fordelingssannsynlighet mellom nedre grense og øvre grense for spesifiserte df (frihetsgrader). Du kan klikke på Tegn (Skyggelegg område) i kontrollboksen for å skyggelegge området mellom nedre og øvre grense. Endringer som du foretar i opprinnelig nedre grense og øvre grense oppdaterer fordelingen automatisk.
Denne fordelingen er nyttig når du vil bestemme sannsynligheten for forekomsten av en verdi innenfor et intervall som er definert av en nedre og en øvre grense for en normalt fordelt populasjon når populasjonens standardavvik er ukjent.
Invers t (invt)
Beregner invers kumulativ sannsynlighetsfunksjon for t-fordeling spesifisert av frihetsgrad, df, for et gitt område under kurven.
Denne fordelingen er nyttig når du vil bestemme sannsynligheten for en forekomst av data i arealet fra 0 til x<1. Denne funksjonen brukes når populasjonsgjennomsnitt og/eller populasjonsstandardavvik ikke er kjent.
c2 Pdf (c2 Pdf())
Beregner funksjonen for sannsynlighetstetthet (pdf) for c2 (chi-kvadrat) fordelingen ved en spesifisert x-verdi. df (frihetsgrader) må være et heltall > 0. Funksjonen for sannsynlighetstetthet (pdf) er:
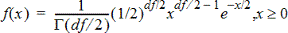
Denne fordelingen er nyttig når du vil bestemme sannsynligheten for forekomsten av en gitt verdi fra en populasjon med en c2-fordeling. Tegne-alternativet er tilgjengelig når c2 Pdf aktiveres fra en formelcelle.
c2 Cdf (c2 Cdf())
Beregner c2 (chi-kvadrat) fordelingssannsynlighet mellom nedreGrense ogøvreGrense for spesifisert df (frihetsgrader). Du kan klikke på Tegn Skyggelegg område i avmerkingsboksen for å skyggelegge området mellom nedre og øvre grense. Endringer som du foretar i opprinnelig nedreGrense og øvreGrense oppdaterer fordelingen automatisk.
Denne fordelingen er nyttig når du vil bestemme sannsynligheten for forekomsten av verdi innenfor gitte grenser for en populasjon med en c2-fordeling.
F Pdf (F Pdf())
Beregner funksjonen for sannsynlighetstetthet (pdf) for F fordeling ved en spesifisert x-verdi. teller df (frihetsgrader) og nevner df må være heltall 0. Funksjonen for sannsynlighetstetthet (pdf) er:

|
der |
n = teller, antall frihetsgrader |
Denne fordelingen er nyttig når du vil bestemme sannsynligheten for at to utvalg har samme varians. Tegne-alternativet er tilgjengelig nårF Pdf aktiveres fra en formelcelle.
F Cdf (F Cdf())
Beregner F fordelingssannsynligheten mellom nedreGrense og øvreGrense for spesifisert dfTeller (frihetsgrader) og dfNevner. Du kan klikke på Tegn (Skyggelegg område) i avmerkingsboksen for å skyggelegge området mellom nedre og øvre grense. Endringer som du foretar i opprinnelig nedreGrense og øvreGrense oppdaterer fordelingen automatisk.
Denne fordelingen er nyttig når du vil bestemme sannsynligheten for at en enkelt observasjon faller innenfor området mellom nedre grense og øvre grense.
Binomisk Pdf (binomPdf())
Beregner en sannsynlighet ved x for diskret binomisk fordeling med spesifiserte antforsøk og suksess-sannsynlighet (p) ved hvert forsøk. x-parameteren kan være et heltall eller en liste med heltall. 0{p{1 må være sann. antforsøk må være et heltall > 0. Hvis du ikke spesifiserer x, returneres en liste med sannsynligheter fra 0 til antforsøk. Funksjonen for sannsynlighetstetthet (pdf) er:
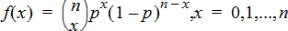
der n = antforsøk
Denne fordelingen er nyttig når du vil bestemme sannsynligheten for å lykkes x ganger i løpet av n forsøk. Du kan for eksempel bruke denne fordelingen til å forutsi sannsynligheten for å kaste krone på det 5. kastet når du kaster kron og mynt.
Binomisk Cdf (binomCdf())
Beregner en kumulativ sannsynlighet for diskret binomisk fordeling med n antall forsøk og sannsynlighet p for suksess ved hvert forsøk.
Denne fordelingen er nyttig når du vil finne sannsynligheten for å lykkes ved minst ett forsøk før alle forsøkene er fullført. Hvis for eksempel krone er et vellykket myntkast og du planlegger å kaste mynten 10 ganger, kan denne fordelingen forutsi sjansen for å få krone minst én gang i løpet av de 10 kastene.
Invers binomial (invBinom())
Gitt antall forsøk (NumTrials) og sannsynligheten for å lykkes for hvert forsøk (Prob), Denne funksjonen returnerer minimum antall suksesser, k, slik at verdien, k, er større eller lik den oppgitte kumulative sannsynligheten (CumulativeProb).
Denne fordelingen er nyttig for å fastslå øvre grense for inndata for binomial cdf. Hvis du for eksempel kaster mynt og krone ti ganger, og du vil ha sannsynligheten for å få x kroner eller mindre til å være under 75 %, hjelper denne fordelingen med å fastslå hva x bør være.
Invers binomisk med hensyn på NinvBinomN())
Gitt sannsynligheten for å lykkes med hvert forsøk (Prob), og antall suksesser (NumSuccess), returnerer denne funksjonen minimum antall forsøk, N, slik at verdien, N, er mindre eller lik kumulativ sannsynlighet (CumulativeProb).
Denne fordelingen er nyttig for å fastslå antall forsøk for binomial cdf. Hvis du for eksempel kaster mynt og krone flere ganger og du ønsker at antall kroner skal være seks eller færre med en sannsynlighet på mindre enn 25 %, hjelper denne fordelingen med å fastslå hvor mange ganger du skal kaste mynt og krone.
Poisson Pdf (poissPdf())
Beregner en sannsynlighet ved x for den diskrete Poisson-fordelingen med spesifisert gjennomsnitt, µ, som må være et reelt tall > 0. x kan være et heltall eller en liste av heltall. Funksjonen for sannsynlighetstetthet (pdf) er:
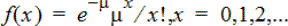
Denne fordelingen er nyttig når du vil finne sannsynligheten for å oppnå et visst antall vellykkede resultater før et forsøk begynner. Du kan for eksempel bruke denne beregningen til å anslå hvor mange ganger du vil få krone når du kaster en mynt 8 ganger.
Poisson Cdf (poissCdf())
Beregner en kumulativ sannsynlighet for den diskrete Poisson-fordeling med spesifisert gjennomsnitt, x.
Denne beregningen er nyttig når du vil finne sannsynligheten for at et visst antall vellykkede forsøk opptrer mellom den øvre og den nedre grensen i et forsøk. Du kan for eksempel bruke denne beregningen til å forutsi hvor mange ganger du kaster krone mellom myntkast nr. 3 og myntkast nr. 8.
Geometrisk Pdf (geomPdf())
Beregner en sannsynlighet ved x, antall forsøk før første suksess inntreffer, for diskret geometrisk fordeling med spesifisert sannsynlighet for suksess p 0{p{1 må være sann. x kan være et heltall eller en liste med heltall. Funksjonen for sannsynlighetstetthet (pdf) er:

Denne fordelingen er nyttig når du vil finne det mest sannsynlige antallet forsøk før du oppnår et vellykket kast. Du kan for eksempel bruke denne beregningen for å anslå hvor mange ganger du må kaste mynten før du får krone første gang.
Geometrisk Cdf (geomCdf())
Beregner en kumulativ geometrisk sannsynlighet fra nedreGrense til øvreGrense med den spesifiserte suksess-sannsynligheten, p.
Denne fordelingen er nyttig når du vil finne sannsynligheten som er assosiert med den første suksessen som inntreffer i løpet av forsøkene fra 1 til n. Du kan for eksempel bruke denne beregningen for å bestemme sannsynligheten for at du får krone første gang på kast nr. 1, nr. 2, nr. 3, ..., nr. n.