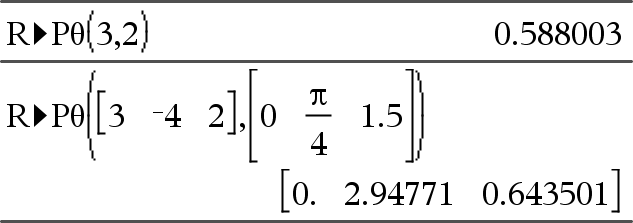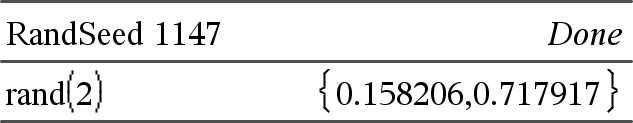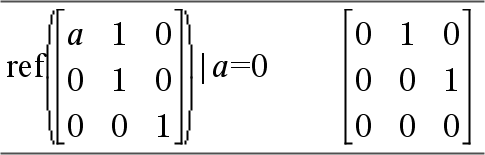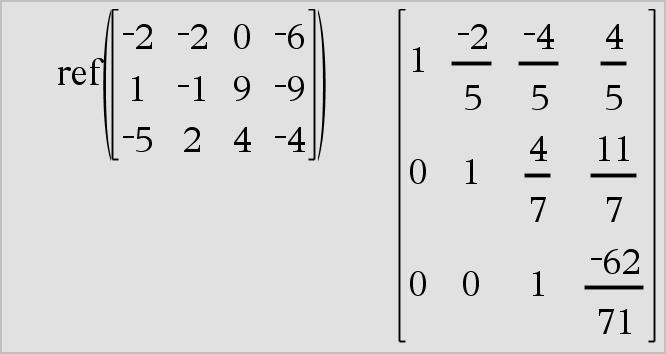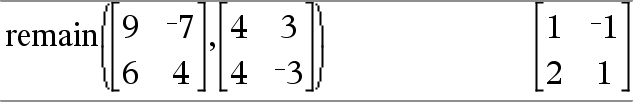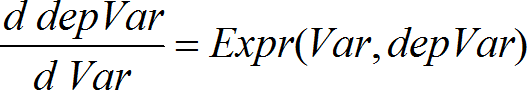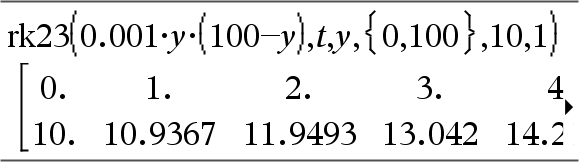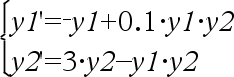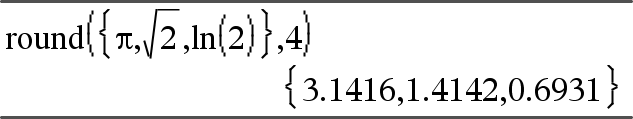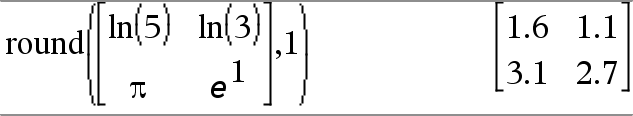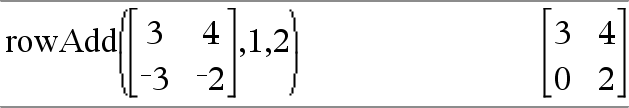R

R►Pθ()

Katalog >


R►Pθ (xValue, yValue) ⇒ värde
R►Pθ (xList, yList) ⇒ lista
R►Pθ (xMatrix, yMatrix) ⇒ matris

Ger den ekvivalenta θ-koordinaten för
(x,y) värden.

Obs: Resultatet erhålls som en vinkel i grader, nygrader eller radianer för respektive inställning av vinkelenhet.

Obs: Du kan infoga denna funktion med datorns tangentbord genom att skriva R@Ptheta(...).

Med vinkelmått Grader:


Med vinkelenhet Nygrader:


Med vinkelenhet Radianer:

R►Pr()

Katalog >


R►Pr (xValue, yValue) ⇒ värde
R►Pr (xList, yList) ⇒ lista
R►Pr (xMatrix, yMatrix) ⇒ matris

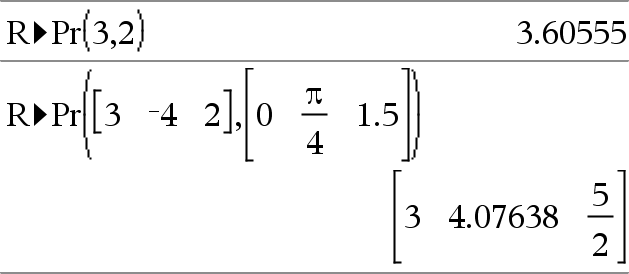
Ger den ekvivalenta r-koordinaten för argumentparen (x,y).

Obs: Du kan infoga denna funktion med datorns tangentbord genom att skriva R@Pr(...).

Med vinkelenhet Radianer:

►Rad

Katalog >

Value1►Rad ⇒ värde

Konverterar argumentet till en vinkel i radianer.

Obs: Du kan infoga denna operator med datorns tangentbord genom att skriva @>Rad.

Med vinkelmått Grader:


Med vinkelenhet Nygrader:

rand( )

Katalog >

rand( ) ⇒ uttryck
rand(#Trials) ⇒ lista

rand( ) ger ett slumpvärde mellan 0 och 1.

rand(#Trials) ger en lista med #Trials slumpvärden mellan 0 och 1.

Bestämmer slumptalsfröet.

slumpBin( )

Katalog >

randBin(n, p) ⇒ uttryck
randBin(n, p, #Trials) ⇒ lista

randBin(n, p) ger ett reellt slumptal från en specificerad binomialfördelning.

randBin(n, p, #Trials) ger en lista med #Trials reella slumptal från en specificerad binomialfördelning.

slumpBin( )

Katalog >

randInt(lowBound,upBound) ⇒ uttryck
randInt(lowBound,upBound ,#Trials) ⇒ lista

randInt(lowBound,upBound) ger ett slumptal med heltalsvärde inom det område som specificeras av heltalsgränserna lowBound och upBound.

randInt(lowBound,upBound,#Trials) ger en lista med #Trials slumptal med heltalsvärden inom det specificerade området.

randMat( )

Katalog >

randMat(numRows, numColumns) ⇒ matris

Ger en matris med heltal mellan -9 och 9 med specificerad dimension.

Båda argumenten måste förenklas till heltal.

Obs: Värdena i denna matris ändras varje gång du trycker på ·.

slumpNorm( )

Katalog >

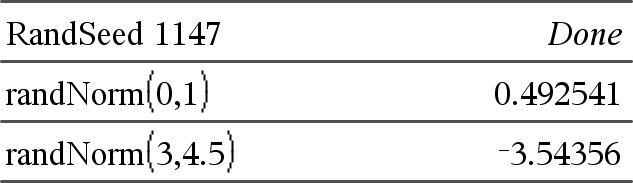
randNorm(μ, σ) ⇒ uttryck
randNorm(μ, σ, #Trials) ⇒ lista

randNorm(μ, σ) ger ett decimalt tal från den specificerade normalfördelningen. Det kan vara ett reellt tal vilket som helst, men det blir kraftigt koncentrerat i intervallet [μ−3•σ, μ+3•σ].

randNorm(μ, σ, #Trials) ger en lista med #Trials decimaltal från den specificerade normalfördelningen.

randPoly()

Katalog >

randPoly(Var, Order) ⇒ uttryck

Ger ett polynom i Var i specificerad Order. Koefficienterna är slumpmässiga heltal i intervallet −9 till 9. Den första koefficienten kommer inte att vara noll.

Order måste vara 0–99.

randSamp( )

Katalog >

randSamp(List,#Trials[,noRepl])⇒ lista

Ger en lista på ett slumpmässigt urval av #Trials försök från List med ett alternativ för återläggning (noRepl=0) eller ingen återläggning(noRepl=1). Förinställningen är med urvalsutbyte.

RandSeed

Katalog >

RandSeed Tal

Om Number = 0 ställs fröna in på fabriksinställningarna för slumptalsgeneratorn. Om Number ≠0, används det för att generera två frön, vilka lagras i systemvariablerna seed1 och seed2.

real( )

Katalog >

real(Value1) ⇒ värde

Ger argumentets reella del.

real(List1) ⇒ lista

Ger de reella delarna av alla element.

real(Matrix1) ⇒ matris

Ger de reella delarna av alla element.

►Rect

Katalog >

Vector ►Rect

Obs: Du kan infoga denna operator med datorns tangentbord genom att skriva @Rect.

Visar Vector i rektangulär form [x, y, z]. Vektorn måste ha dimensionen 2 eller 3 och kan vara en rad eller en kolumn.

Obs: ►Rect är en visa format-instruktion, inte en konverteringsfunktion. Du kan endast använda den i slutet av en inmatningsrad, och den uppdaterar inte ans.

Obs: Se även ►Polar, här.

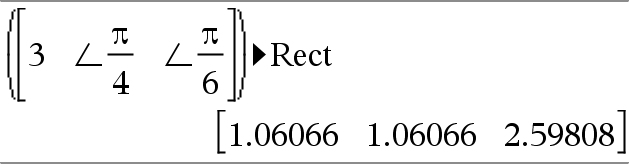
complexValue ►Rect

Visar complexValue i rektangulär form a+bi. complexValue kan ha valfri komplex form. En inmatning av reiθ orsakar dock ett fel i vinkelläget Grader.

Obs: Du måste använda parenteserna för en (r∠θ) polär inmatning.

Med vinkelenhet Radianer:


Med vinkelenhet Nygrader:


Med vinkelmått Grader:

Obs: För att skriva in tecknet ∠, välj det från symbollistan i Katalog.

ref( )

Katalog >

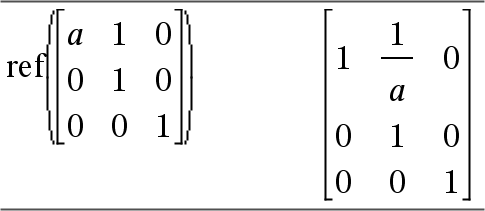
ref(Matrix1[, Tol]) ⇒ matris

Ger radtrappstegsformen av Matrix1.

Alternativt behandlas varje matriselement som noll om dess absolutvärde är mindre än Tol. Denna tolerans används endast om matrisen har inmatning i flyttalsform och inte innehåller några symboliska variabler som inte har tilldelats ett värde. Annars ignoreras Tol.

• Om du använder /·· eller ställer in Auto or Approximate på Approximate, utförs beräkningarna med flyttalsaritmetik.
• Om Tol utelämnas eller inte används beräknas standardtoleransen som:
5E−14 •max(dim(Matrix1)) •rowNorm(Matrix1)

Undvik odefinierade element i Matrix1. De kan leda till oväntade resultat.

Om till exempel a är odefinierat i följande uttryck visas ett varningsmeddelande och resultatet ges som:

Varningen visas på grund av att det generaliserade elementet 1/a inte skulle vara giltigt för a=0.

Du kan undvika detta genom att i förväg lagra ett värde i a eller genom att använda (“|”)-operatorn begränsning för att ersätta ett värde såsom visas i följande exempel.

Obs: Se även rref( ), här.

 

RefreshProbeVars

Katalog >

RefreshProbeVars

Låter dig visa sensordata från alla anslutna sensorer via TI-grundprogrammet.

StatusVar-värde

Status

statusVar=0

Normal (fortsätt med programmet)

statusVar=1

Vernier DataQuest™-applikationen är i datainsamlingsläge.

Obs: Vernier DataQuest™-applikationen måste vara i läge "meter" för att detta kommando ska fungera.

statusVar=2

Vernier DataQuest™-applikationen har inte startats.

statusVar=3

Vernier DataQuest™-applikationen har startats men inga givare har anslutits.

Exempel

Define temp()=

Prgm

© Kontrollera om systemet är klart

RefreshProbeVars status

If status=0 Then

Disp "klar"

För n,1,50

RefreshProbeVars status

temperatur:=mätare.temperatur

Disp "Temperatur: ",temperatur

If temperature>30 Then

Disp "För varm"

EndIf

© Vänta 1 sekund mellan mätningarna

Wait 1

EndFor

Else

Disp "Ej klar. Försök igen senare"

EndIf

EndPrgm

 

Obs: Detta kan även användas med TI-Innovator™ hubb.

 

remain( )

Katalog >


remain(Value1, Value2) ⇒ värde
remain(List1, List2) ⇒ lista
remain(Matrix1, Matrix2) ⇒ matris

Ger resten på det första argumentet med avseende på det andra argumentet definierat av identiteterna:

remain(x,0)   x
remain(x,y)   x−y•iPart(x/y)

Som en följd av detta, observera att remain(−x,y) − remain(x,y). Resultatet är antingen noll eller har samma tecken som det första argumentet.

Obs: Se även mod( ), här.

Request

Katalog >

Begär promptString, var[, DispFlag [, statusVar]]

Request promptString, func(arg1, ...argn)  [, DispFlag [, statusVar]]

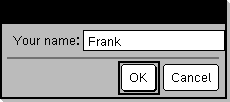
Programmeringskommando: Pausar programmet och visar en dialogruta med meddelandet promptString och en svarsruta där användaren ska skriva in svaret.

När användaren skriver in svaret och klickar på OK tilldelas variabeln vardet värde som står i svarsrutan.

Om användaren klickar på Cancel (Avbryt) fortsätter programmet utan att acceptera någon inmatning. Programmet använder det tidigare värdet på var om var redan var definierad.

Det valfria argumentet DispFlag kan vara ett valfritt uttryck.

• Om DispFlag utelämnas eller beräknas till 1, visas promptmeddelandet och användarens svar i Räknarens historik.
• Om DispFlag beräknas till 0 visas inte prompten och svaret i historiken.

Definiera ett program:

Definiera begär_demo()=Prgm
    Begär ”Radie: ”,r
    Disp ”Area = ”,pi*r2
EndPrgm

 

Kör programmet och skriv in ett svar:

request_demo( )

Resultat efter tryckning på OK:

Radie: 6/2
Area= 28,2743

Det valfria argumentet statusVar ger programmet ett sätt att bestämma hur användaren lämnade dialogrutan. Observera att statusVar är beroende av argumentet DispFlag.

• Om användaren klickade på OK eller tryckte på Enter eller Ctrl+Enter ges variabeln statusVar värdet 1.
• Annars får variabeln statusVar värdet 0.

Med argumentet funk( ) kan programmet lagra användarens svar som en funktionsdefinition. Denna syntax fungerar som om användaren exekverade kommandot:

     Definiera funk(arg1, ...argn) = användarens svar

Programmet kan sedan använda den definierade funktionen func(). Strängen promptString bör vägleda användaren till att skriva in ett lämpligt användarsvar som fullbordar funktionsdefinitionen.

Obs: Du kan använda Request -kommandot med ett användardefinierat program, men inte inom en funktion.

För att stoppa ett program som innehåller ett Request-kommando inne i en oändlig slinga:

• Handenhet: Håll ned c och tryck på · upprepade gånger.
• Windows®: Håll ned F12 och tryck på Enter upprepade gånger.
• Macintosh®: Håll ned F5 och tryck på Enter upprepade gånger.
• iPad®: Appen visar en uppmaning. Du kan fortsätta att vänta eller avbryta.

Obs: Se även RequestStr, här.

Definiera ett program:

Definiera polynom()=Prgm
    Request "Skriv in ett polynom i x:",p(x)
    Disp "Reella rötter är:",polyRoots(p(x),x)
EndPrgm

 

Kör programmet och skriv in ett svar:

polynom()

Resultat efter inmatning av x^3+3x+1 och tryckning på OK:

Reella rötter är: {-0,322185}

RequestStr

Katalog >

RequestStr promptString, var[, DispFlag]

Programmeringskommando: Fungerar på precis samma sätt som den första syntaxen i kommandot Request, förutom att användarens svar alltid tolkas som en sträng. Kommandot Request tolkar svaret som ett uttryck såvida inte användaren omger det med citationstecken ("").

Obs: Kommandot RequestStr kan användas inom ett användardefinierat program, men inte inom en funktion.

Att stoppa ett program som innehåller ett RequestStr-kommando i en oändlig loop:

• Handenhet: Håll ned c och tryck på · upprepade gånger.
• Windows®: Håll ned F12 och tryck på Enter upprepade gånger.
• Macintosh®: Håll ned F5 och tryck på Enter upprepade gånger.
• iPad®: Appen visar en uppmaning. Du kan fortsätta att vänta eller avbryta.

Obs: Se även Request, här.

Definiera ett program:

Definiera requestStr_demo()=Prgm
    BegärStr "Ditt namn:",namn,0
    Disp “Svaret har “,dim(namn),” tecken.”
EndPrgm

 

Kör programmet och skriv in ett svar:

begärStr_demo()

 

Resultat efter tryckning på OK (observera att argumentet DispFlag för 0 förbiser prompten och svarar från historiken):

 

begärStr_demo()

Svaret har 5 tecken.

Return

Katalog >

Return [Expr]

Ger Expr som resultatet av funktionen. Använd inom ett Func...EndFunc-block.

Obs: Använd Return utan ett argument inom ett Prgm...EndPrgm-block för att gå ur ett program.

Obs för att mata in exemplet: Se avsnittet Räknare i produkthandboken för instruktioner om hur du anger multiline-program och funktionsdefinitioner.

right()

Katalog >

right(List1[, Num]) ⇒ lista

Ger Num-elementen längst till höger i List1.

Om du utelämnar Num erhålls alla i List1.

right(sourceString[, Num]) ⇒ sträng

Ger Num-tecknen längst till höger i teckensträngen sourceString.

Om du utelämnar Num erhålls alla i sourceString.

right(Comparison) ⇒ uttryck

Ger den högra sidan av en ekvation eller olikhet.

rk23 ()

Katalog >

rk23(Expr, Var, depVar, {Var0, VarMax}, depVar0, VarStep [, diftol]) ⇒ matris

rk23(SystemOfExpr, Var, ListOfDepVars, {Var0, VarMax}, ListOfDepVars0, VarStep[, diftol]) ⇒ matrix

rk23(ListOfExpr, Var, ListOfDepVars, {Var0, VarMax}, ListOfDepVars0, VarStep[, diftol]) ⇒ matrix

Använder Runge-Kuttas metod för att lösa systemet

med depVar(Var0)=depVar0 i intervallet [Var0,VarMax]. Ger en matris vars första rad definierar resultatvärdena för Var, definierade av VarStep. Den andra raden definierar värdet på den första lösningskomponenten vid motsvarande värden på Var, och så vidare.

Expr är det högra ledet som definierar den ordinära differentialekvationen (ODE).

SystemOfExpr är ett system av högerled som definierar systemet av ODE:er (motsvarar ordningen av oberoende variabler i ListOfDepVars).

ListOfExpr är en lista på högerled som definierar systemet av ODE:er (motsvarar ordningen av oberoende variabler i ListOfDepVars).

Var är den oberoende variabeln.

ListOfDepVars är en lista på oberoende variabler.

{Var0, VarMax} är en lista med två element som instruerar funktionen att integrera från Var0 till VarMax.

ListOfDepVars0 är en lista på startvärden för oberoende variabler.

Om VarStep utvärderas till ett tal skilt från noll ges sign(VarStep) = sign(VarMax-Var0) och lösningar vid Var0+i*VarStep för alla i=0,1,2,… sådana att Var0+i*VarStep är i intervallet [var0,VarMax] (kanske inte ger ett lösningsvärde vid VarMax).

Om VarStep utvärderas till noll ges lösningar vid "Runge-Kutta"-värdena för Var.

diftol är feltoleransen (förinställs på 0,001).

Differentialekvation:

y'=0,001*y*(100-y) och y(0)=10

För att se hela resultatet, tryck på 5 och använd sedan 7 och 8 för att flytta markören.

Samma ekvation med diftol inställd på 1.E−6

Ekvationssystem:

med y1(0)=2 och y2(0)=5

Rot()

Katalog >

root(Value) ⇒ root
root(Value1, Value2) ⇒ root

root(Value) ger kvadratroten ur Value.

root(Value1, Value2) ger Value2-roten ur Value1. Value1 kan vara en reell eller komplex konstant i flyttalsform, ett heltal eller komplex rationell konstant.

Obs: Se även Nth root template, här.

rotate()

Katalog >

rotate(Integer1[,#ofRotations]) ⇒ heltal

Roterar bitarna i ett binärt heltal. Integer1 kan anges i valfri talbas. Det omvandlas automatiskt till 64 positioners binär form. Om storleken på Integer1 är alltför stor för denna form, för en symmetrisk modulooperation talet inom området. För mer information, se ►Base2,  här.

I binärt basläge:

 

För att se hela resultatet, tryck på 5 och använd sedan 7 och 8 för att flytta markören.

Om #ofRotations är positiv sker rotationen åt vänster. Om #ofRotations är negativ sker rotationen åt höger. Förinställningen är −1 (rotera en position åt höger).

Vid exempelvis rotation åt höger:

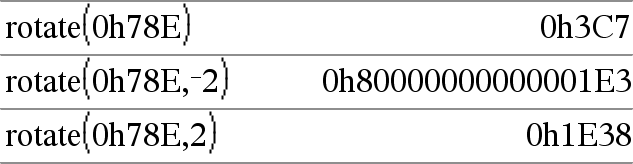
I hexadecimalt basläge:

Varje bit roteras åt höger.

0b00000000000001111010110000110101

Biten längst till höger roteras till positionen längst till vänster.

ger:

0b10000000000000111101011000011010

Resultatet visas enligt det inställda basläget.

Viktigt: För att skriva in ett binärt eller hexadecimalt tal, använd alltid prefixet 0b eller 0h (noll, inte bokstaven O).

rotate(List1[,#ofRotations]) ⇒ lista

Ger en kopia av List1 roterad åt höger eller vänster av #ofRotations-elementen. Ändrar inte List1.

Om #ofRotations är positiv sker rotationen åt vänster. Om #ofRotations är negativ sker rotationen åt höger. Förinställningen är −1 (rotera ett element åt höger).

I decimalt basläge:

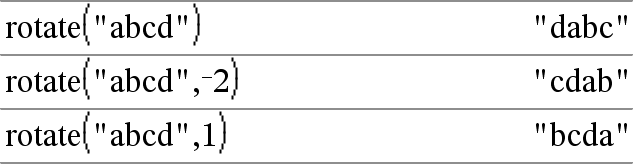
rotate(String1[,#ofRotations]) ⇒ sträng

Ger en kopia av String1 roterad åt höger eller vänster av #ofRotations-tecknen. Ändrar inte String1.

Om #ofRotations är positiv sker rotationen åt vänster. Om #ofRotations är negativ sker rotationen åt höger. Förinställningen är −1 (rotera ett tecken åt höger).

round()

Katalog >

round(Value1[, digits]) ⇒ värde

Ger argumentet avrundat till det specificerade antalet siffror efter decimalpunkten.

digits måste vara ett heltal i intervallet 0–12. Om digits inte ingår, ges argumentet avrundat till 12 signifikanta siffror.

Obs: Läget Display digits (Visa siffror) kan påverka hur detta visas.

round(List1[, digits]) ⇒ lista

Ger en lista på elementen avrundade till det specificerade antalet siffror.

round(Matrix1[, digits]) ⇒ matris

Ger en matris över elementen avrundade till det specificerade antalet siffror.

rowAdd()

Katalog >

rowAdd(Matrix1, rIndex1, rIndex2) ⇒ matris

Ger en kopia av Matrix1 med rad rIndex2 ersatt av summan av raderna rIndex1 och rIndex2.

rowDim()

Katalog >

rowDim(Matrix) ⇒ uttryck

Ger antalet rader i Matrix.

Obs: Se även colDim(), här.

rowNorm()

Katalog >

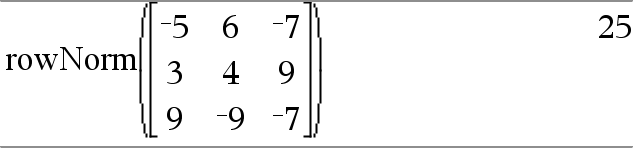
rowNorm(Matrix) ⇒ uttryck

Ger maximum av summorna av absolutbeloppen på elementen i raderna i Matrix.

Obs: Alla matriselement måste förenklas till tal. Se även colNorm(), här.

rowSwap()

Katalog >

rowSwap(Matrix1, rIndex1, rIndex2) ⇒ matris

Ger Matrix1 med raderna rIndex1 och rIndex2 växlade.

rref()

Katalog >

rref(Matrix1[, Tol]) ⇒ matris

Ger den reducerade radtrappstegsformen av Matrix1.

Alternativt behandlas varje matriselement som noll om dess absolutvärde är mindre än Tol. Denna tolerans används endast om matrisen har inmatning i flyttalsform och inte innehåller några symboliska variabler som inte har tilldelats ett värde. Annars ignoreras Tol.

• Om du använder / eller ställer in Auto or Approximate på Approximate, utförs beräkningarna med flyttalsaritmetik.
• Om Tol utelämnas eller inte används beräknas standardtoleransen som:
5E−14 •max(dim(Matrix1)) •rowNorm(Matrix1)

Obs: Se även ref( ), här.