|
Katalog > |
||||||||||
|
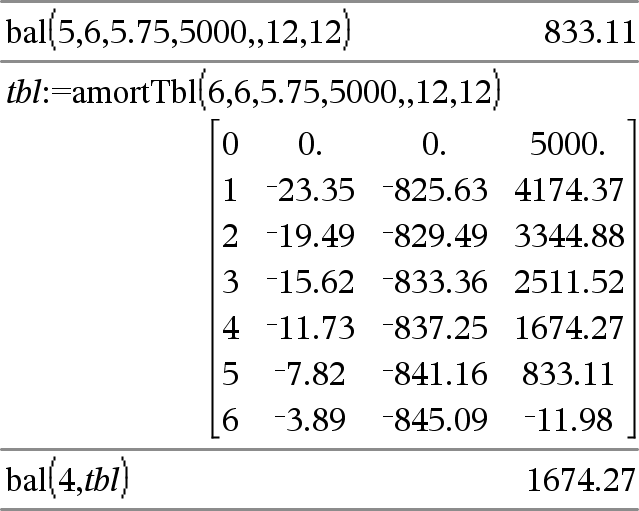
bal(NPmt,N,I,PV,[Pmt], [FV], [PpY], [CpY], [PmtAt], [roundValue])Þvärde bal(NPmt,amortTable)Þvärde Amorteringsfunktion som beräknar planerad balans efter en specificerad inbetalning. N, I, PV, Pmt, FV, PpY, CpY och PmtAt beskrivs i tabellen över TVM-argument, se här. NPmt anger numret på den inbetalning efter vilken du vill att data skall beräknas. N, I, PV, Pmt, FV, PpY, CpY och PmtAt beskrivs i tabellen över TVM-argument, se här.
roundValue anger antalet decimaler för avrundning. Förinställning: 2. bal(NPmt,amortTable) beräknar lånebalansen efter inbetalning nummer NPmt, baserat på amorteringstabell amortTable. Argumentet amortTable måste vara en matris i den form som beskrivs under amortTbl(), här. Obs: Se även GInt() och GPrn(), här. |
|
|
Katalog > |
|
|
Integer1 4Base2Þheltal Obs: Du kan infoga denna operator med datorns tangentbord genom att skriva @>Base2. Omvandlar Integer1 till ett binärt tal. Binära och hexadecimala tal har alltid prefixet 0b respektive 0h. Noll, inte bokstaven O, följt av b eller h. 0b binärtTal 0h hexadecimaltTal |
|
|
Ett binärt tal kan ha upp till 64 siffror. Ett hexadecimalt tal kan ha upp till 16 siffror. Utan prefix behandlas Integer1 som ett decimalt tal (bas 10). Resultatet visas i binär form, oavsett Bas-läget. Negativa tal visas i “tvåkomplement”-form. Exempel, N1 visas som 0hFFFFFFFFFFFFFFFF i Hexadecimalt basläge 0b111...111 (64 1’s) i Binärt basläge N263 visas som 0h8000000000000000 i Hexadecimalt basläge 0b100...000 (63 zeros) i Binärt basläge Om du skriver in ett decimalt heltal som är alltför stort för att anges i 64-bitars binär form används en symmetrisk modulooperation för att få ned värdet till lämplig nivå. Se följande exempel på värden utanför området. 263 blir N263 och visas som 0h8000000000000000 i Hexadecimalt basläge 0b100...000 (63 nollor) i Binärt basläge 264 blir 0 och visas som 0h0 i Hexadecimalt basläge 0b0 i Binärt basläge N263 N 1 blir 263 N 1 och visas som 0h7FFFFFFFFFFFFFFF i Hexadecimalt basläge 0b111...111 (64 ettor) i Binärt basläge |
|
|
Katalog > |
|
|
Integer1 4Base10Þheltal Obs: Du kan infoga denna operator med datorns tangentbord genom att skriva @>Base10. Omvandlar Integer1 till ett decimalt tal (bas 10). En binär eller hexadecimal inmatning måste alltid ha prefixet 0b respektive 0h. 0b binaryNumber 0h hexadecimalNumber Noll, inte bokstaven O, följt av b eller h. Ett binärt tal kan ha upp till 64 siffror. Ett hexadecimalt tal kan ha upp till 16 siffror. Utan prefix behandlas Integer1 som ett decimalt tal. Resultatet visas i decimal form, oavsett Bas-läget. |
|
|
Katalog > |
|
|
Integer1 4Base16Þheltal Obs: Du kan infoga denna operator med datorns tangentbord genom att skriva @>Base16. Konverterar Integer1 till ett hexadecimalt tal. Binära och hexadecimala tal har alltid prefixet 0b respektive 0h. 0b binaryNumber 0h hexadecimalNumber Noll, inte bokstaven O, följt av b eller h. Ett binärt tal kan ha upp till 64 siffror. Ett hexadecimalt tal kan ha upp till 16 siffror. Utan prefix behandlas Integer1 som ett decimalt tal (bas 10). Resultatet visas i hexadecimal form, oavsett Bas-läget. Om du skriver in ett decimalt heltal som är alltför stort för att anges i 64-bitars binär form används en symmetrisk modulooperation för att få ned värdet till lämplig nivå. För mer information, se 4Base2, här. |
|
|
Katalog > |
|
|
binomCdf(n,p)Þlista binomCdf(n,p,lowBound,upBound)Þtal om lowBound och upBound är tal, lista om lowBound och upBound är listor binomCdf(n,p,upBound)för P(0{X{upBound)Þtal om upBound är ett tal, lista om upBound är en lista Beräknar en kumulativ sannolikhet för den diskreta binomialfördelningen med n antal försök och sannolikheten p för att lyckas vid varje försök. För P(X { upBound), sätt lowBound=0 |
|
|
Katalog > |
|
|
binomPdf(n,p)Þlista binomPdf(n,p,XVal)Þtal om XVal är ett tal, lista om XVal är en lista Beräknar en sannolikhet för den diskreta binomialfördelningen med n antal försök och sannolikheten p för att lyckas vid varje försök. |
|