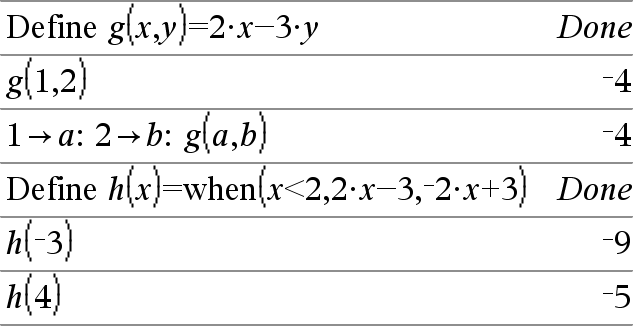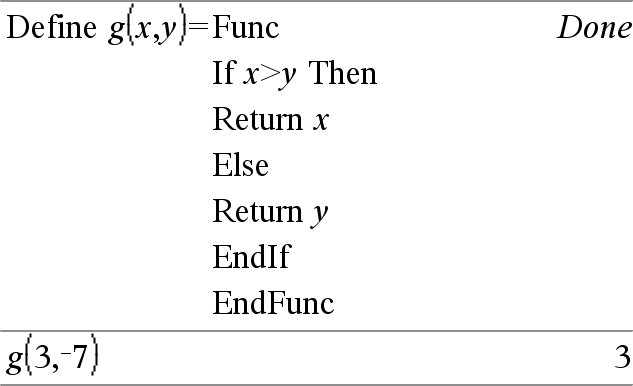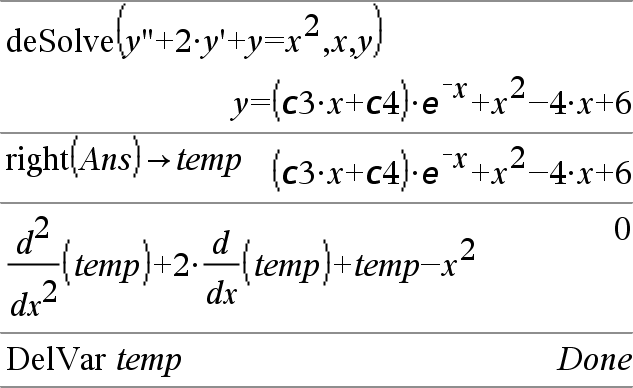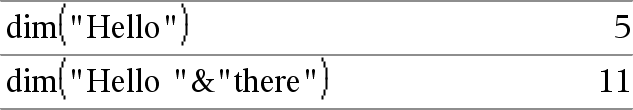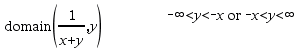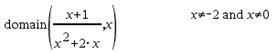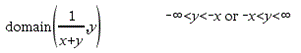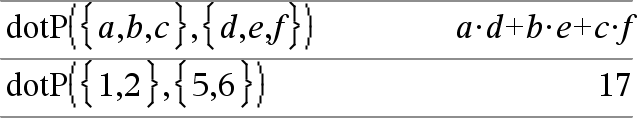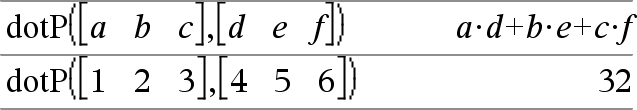|
Catalogus > |
|
|
dbd(datum1,datum2)Þwaarde Geeft het aantal dagen tussen datum1 en datum2 met behulp van de actuele-dag-telmethode. datum1 en datum2 kunnen getallen of lijsten met getallen zijn binnen het bereik van de datums op de standaard kalender. Als zowel datum1 als datum2 lijsten zijn, dan moeten deze dezelfde lengte hebben. datum1 en datum2 moeten tussen de jaren 1950 tot en met 2049 liggen. U kunt de datums in twee notaties invoeren. De plaatsing van de decimale punt onderscheidt de datumnotaties. MM.DDJJ (algemeen gebruikte notatie in de Verenigde Staten) DDMM.JJ (algemeen gebruikte notatie in Europa) |
|
|
Catalogus > |
|
|
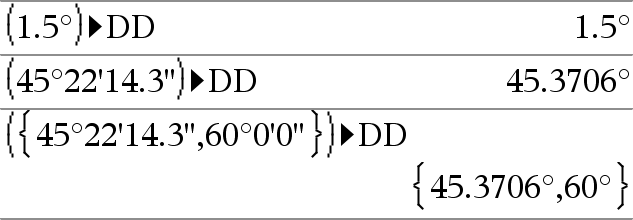
Uitdr1 4DDÞwaarde Lijst1 4DDÞlijst Matrix1 4DDÞmatrix Opmerking: u kunt deze operator vanaf het toetsenbord van de computer invoeren door @>DD in te typen. Geeft het decimale equivalent van het argument, uitgedrukt in graden. Het argument is een getal, lijst of matrix die op basis van de hoekmodus-instelling geïnterpreteerd wordt als decimale graden, radialen of graden. |
In de hoekmodus Graden:
In de hoekmodus Decimale graden:
In de hoekmodus Radialen:
|
|
Catalogus > |
|
|
Lijst1 4DecimalÞuitdrukking Matrix1 4DecimalÞuitdrukking Opmerking: u kunt deze operator vanaf het toetsenbord van de computer invoeren door @>Decimal in te typen. Geeft het argument in decimale vorm weer. Deze operator kan alleen op het eind van de invoerregel gebruikt worden. |
|
|
Catalogus > |
|
|
Define Var = Uitdrukking Define Functie(Param1, Param2, ...) = Uitdrukking Definieert de variabele Var of de door de gebruiker gedefinieerde functie Functie. Parameters, zoals Param1, vormen de plaats voor het doorgeven van argumenten aan de functie. Bij het oproepen van een door de gebruiker gedefinieerde functie moet u argumenten opgeven (bijvoorbeeld waarden of variabelen) die overeenkomen met de parameters. De functie werkt, wanneer deze wordt aangeroepen, Uitdrukking uit met de opgegeven argumenten. Var en Functie kunnen niet de naam van een systeemvariabele of van een ingebouwde functie of commando zijn. Opmerking: deze vorm van Define staat gelijk aan het uitvoeren van de uitdrukking: uitdrukking & Functie(Param1,Param2). |
|
|
Define Functie(Param1, Param2, ...) = Func Define Programma(Param1, Param2, ...) = Prgm In deze vorm kan de door de gebruiker gedefinieerde functie of programma een blok van meerdere beweringen uitvoeren. Blok kan zowel een enkele bewering als een serie beweringen op aparte regels zijn. Blok kan ook uitdrukkingen en instructies (zoals If, Then, Else en For) bevatten. Opmerking bij het invoeren van het voorbeeld: Instructies over het invoeren van programma's met meerdere regels en functiedefinities vindt u in het hoofdstuk Rekenmachine van de handleiding van uw product. Opmerking: Zie ook Define LibPriv, hier en Define LibPub, hier. |
|
|
Catalogus > |
|
|
Define LibPriv Var = Uitdrukking Define LibPriv Functie(Param1, Param2, ...) = Uitdrukking Define LibPriv Functie(Param1, Param2, ...) = Func Define LibPriv Programma(Param1, Param2, ...) = Prgm Werkt hetzelfde als Define, behalve dat er een persoonlijke bibliotheekvariabele, -functie of -programma wordt gecreëerd. Persoonlijke functies en programma's verschijnen niet in de Catalogus. |
|
|
Catalogus > |
|
|
Define LibPub Var = Uitdrukking Define LibPub Functie(Param1, Param2, ...) = Uitdrukking Define LibPub Functie(Param1, Param2, ...) = Func Define LibPub Programma(Param1, Param2, ...) = Prgm Werkt hetzelfde als Define, behalve dat er een openbare bibliotheekvariabele, -functie of -programma wordt gecreëerd. Openbare functies en programma verschijnen in de Catalogus nadat de bibliotheek is opgeslagen en vernieuwd. |
|
|
Zie @List(), hier. |
|
|
|
|
|
Zie @tmpCnv(), hier. |
|
|
|
|
|
Catalogus > |
|
|
DelVar Var1[, Var2] [, Var3] ... DelVar Var. Wist de gespecificeerde variabele of variabelegroep uit het geheugen. Als een aantal van de variabelen vergrendeld is, veroorzaakt deze opdracht een foutmelding en worden alleen de niet-vergrendelde variabelen gewist. Zie |
|
|
DelVar Var. wist alle leden van de variabelegroep Var. (zoals de statistische stat.nn-resultaten of variabelen die gecreëerd zijn met de LibShortcut()-functie). De punt (.) in deze vorm van het commando DelVar beperkt dit tot het wissen van een variabelegroep; de enkelvoudige variabele Var wordt niet gewist. |
|
|
Catalogus > |
|
|
Geeft een lijst met de inhoud van Lijst1 waaruit alle lege elementen verwijderd zijn. Zie voor meer informatie over lege elementen hier. |
|
|
Zie d(), hier. |
|
|
|
|
|
Catalogus > |
|||||||
|
det(vierkanteMatrix[, Tolerantie])Þuitdrukking Geeft de determinant van vierkanteMatrix. Optioneel wordt elk matrixelement behandeld als nul als de absolute waarde ervan minder dan Tolerantie is. Deze tolerantie wordt alleen gebruikt als de matrix gegevens met een drijvende komma heeft, en geen symbolische variabelen bevat die geen waarde toegekend hebben gekregen. Anders wordt Tolerantie genegeerd.
|
|
|
Catalogus > |
|
|
diag(Lijst)Þmatrix diag(rijMatrix)Þmatrix diag(kolomMatrix)Þmatrix Geeft een matrix met de waarden in de argumentenlijst of de argumentenmatrix op zijn hoofddiagonaal. |
|
|
diag(vierkanteMatrix)ÞrijMatrix Geeft een rijmatrix met de elementen uit de hoofddiagonaal van vierkanteMatrix. vierkanteMatrix moet vierkant zijn. |
|
|
Catalogus > |
|
|
dim(Lijst)Þgeheel getal Geeft de afmeting van Lijst. |
|
|
dim(Matrix)Þlijst Geeft de afmetingen van matrix als een lijst met twee elementen {rijen, kolommen}. |
|
|
dim(String)Þgeheel getal Geeft het aantal tekens in de tekenreeks String. |
|
|
Catalogus > |
|
|
Disp uitdrOfString1 [, uitdrOfString2] ... Geeft de argumenten in de geschiedenis van de Rekenmachine. De argumenten worden achter elkaar weergegeven, met smalle spaties als scheiding. Vooral handig in programma's en functies om de weergave van tussenberekeningen te verzekeren. Opmerking bij het invoeren van het voorbeeld: Instructies over het invoeren van programma's met meerdere regels en functiedefinities vindt u in het hoofdstuk Rekenmachine van de handleiding van uw product. |
|
|
Catalogus > |
|||||
|
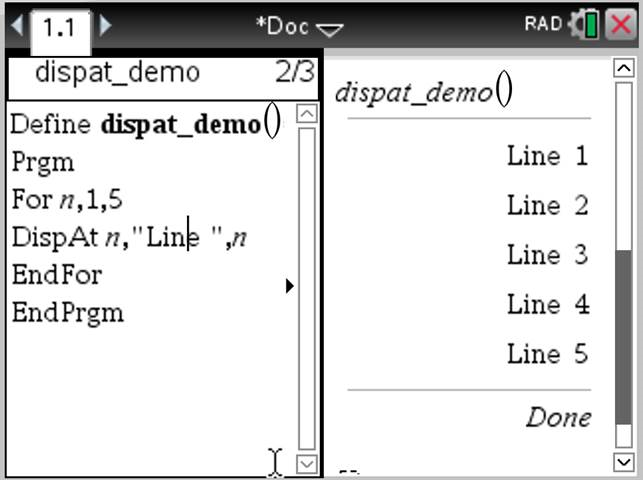
DispAt int,expr1 [,expr2 ...] ... DispAt stelt u in staat de regel op te geven waarin de gespecificeerde uitdrukking of string op het scherm zal worden weergegeven. Het regelnummer kan worden opgegeven als een uitdrukking. Let op: het regelnummer geldt niet voor het gehele scherm, maar voor het gedeelte dat direct volgt op de instructie /het programma. Deze instructie maakt dashboard-achtige uitvoer mogelijk van programma’s waarbij de waarde van een uitdrukking of van een sensor-uitlezing op dezelfde regel wordt bijgewerkt. DispAten Disp kunnen binnen hetzelfde programma worden gebruikt. Opmerking: Het maximale aantal is ingesteld op 8, aangezien dit overeenkomt met een scherm vol met regels op het rekenmachinescherm - zo lang de regels maar geen 2D wiskundige uitdrukkingen bevatten. Het exacte aantal regels is afhankelijk van de inhoud van de weergegeven informatie.
|
Voorbeeld
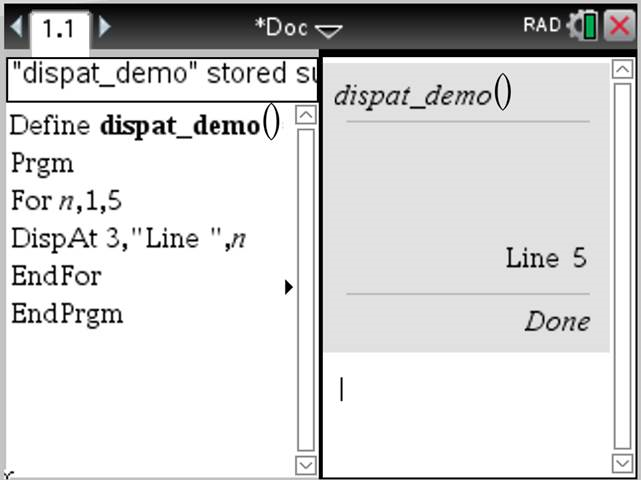
Illustratieve voorbeelden:
|
Foutmeldingen:
|
Foutbericht |
Beschrijving |
|---|---|
|
Het DispAt regelnummer moet tussen de 1 en 8 liggen |
Uitdrukking beoordeelt het Regelnummer buiten het bereik van 1-8 (inclusief 8) |
|
Te weinig argumenten |
In de functie of instructie ontbreken één of meer argumenten. |
|
Geen argumenten |
Hetzelfde als huidige 'syntax error' dialoog |
|
Te veel argumenten |
Beperk argument. Dezelfde error als Disp. |
|
Ongeldig gegevenstype |
Eerste argument moet een getal zijn. |
|
Leeg: DispAt leeg |
De "Hello World"-gegevenstypefout wordt gegeven voor "void" (indien 'terugbellen' is gedefinieerd) |
|
Conversie-operator: DispAt 2_ft @> _m, "Hallo wereld" |
CAS: Gegevenstypefout wordt gegeven (indien 'terugbellen' is gedefinieerd') Numeriek: Conversie zal uitgewerkt worden en indien het resultaat een geldig argument is, zal DispAt de string afdrukken op de resultatenregel. |
|
Catalogus > |
|
|
Lijst 4DMS Matrix 4DMS Opmerking: u kunt deze operator vanaf het toetsenbord van de computer invoeren door @>DMS in te typen. Interpreteert het argument als een hoek en geeft de equivalente DMS (DDDDDD¡MM'SS.ss'')-waarde weer. Zie ¡, ', '' (hier) voor de DMS (graden, minuten, seconden)-notatie. Opmerking: 4DMS converteert van radialen naar graden als hij wordt gebruikt in de radialenmodus. Als de invoer gevolgd wordt door een gradensymbool ¡, treedt er geen conversie op. U kunt 4DMS alleen op het eind van een invoerregel gebruiken. |
In de hoekmodus Graden:
|
|
Catalogus > |
|
|
domain(Uitdr1, Var)Þuitdrukking Geeft het domein van Uitdr1 ten opzichte van variabele Var. domain() kan worden gebruikt om domeinen van functies te onderzoeken. Het is beperkt tot reële en eindige domeinen. Deze functionaliteit heeft beperkingen vanwege tekortkomingen van de computeralgebra-algoritmes voor vereenvoudigen en oplossen Bepaalde functies kunnen niet worden gebruikt als argumenten voor domain() ongeacht of ze expliciet verschijnen of binnen door de gebruiker gedefinieerde variabelen en functies. In het volgende voorbeeld kan de uitdrukking niet worden vereenvoudigd omdat ‰() een niet-toegestane functie is.
|
|
|
Catalogus > |
|
|
dominantTerm(Uitdr1, Var [, Punt])Þuitdrukking dominantTerm(Uitdr1, Var [, Punt]) | Var>Punt Þuitdrukking dominantTerm(Uitdr1, Var [, Punt]) | Var<Punt Þuitdrukking Geeft de dominante term van een machtreeks-representatie van Uitdr1 uitgewerkt rond Punt. De dominante term is de term die het snelst groeit in de buurt van Var = Punt. De resulterende macht van (Var N Punt) kan een negatieve en/of gebroken exponent hebben. De coëfficiënt van deze macht kan logaritmes bevatten van (Var N Punt) en andere functies van Var die gedomineerd worden door alle machten van (Var N Punt) met hetzelfde teken in de exponent. Punt heeft als standaardwaarde 0. Punt kan ˆ of Nˆ zijn; in die gevallen is de dominante term de term met de grootste exponent van Var in plaats van de kleinste exponent van Var. dominantTerm(…) geeft “dominantTerm(…)” als hij niet in staat is om een dergelijke representatie te bepalen, zoals bij essentiële singulariteiten zoals sin(1/z) bij z=0, eN1/z bij z=0 of ez bij z = ˆ or Nˆ. Als de reeks of één van zijn afgeleiden een sprong-discontinuïteit bij Punt heeft, dan bevat het resultaat waarschijnlijk sub-uitdrukkingen van de vorm sign(…) of abs(…) voor een reële uitbreidingsvariabele of (-1)floor(…angle(…)…) voor een complexe uitbreidingsvariabele, dit is een variabele die eindigt op “_”. Als u de dominante term alleen voor waarden aan één zijde van Punt wilt gebruiken, voeg dan aan dominantTerm(...) de juiste specificatie toe: “| Var > Punt”, “| Var < Punt”, “| “Var | Punt” of “Var { Punt” om een eenvoudiger resultaat te krijgen. dominantTerm() is distributief over 1ste-argument-lijsten en matrices. dominantTerm() is handig als u de eenvoudigst mogelijke uitdrukking wilt weten die asymptotisch is naar een andere uitdrukking als Var " Punt. dominantTerm() is ook handig als het niet duidelijk is wat de graad van de eerste niet-nul-term van een reeks zal zijn, en u niet iteratief wilt gokken, hetzij interactief of via een programmalus. Opmerking: Zie ook reeksen(), hier. |
|
|
Catalogus > |
|
|
dotP(Lijst1, Lijst2)Þuitdrukking Geeft het inwendige product van twee lijsten. |
|
|
dotP(Vector1, Vector2)Þuitdrukking Geeft het inwendige product van twee vectoren. Beide moeten rijvectoren zijn, of beide moeten kolomvectoren zijn. |
|