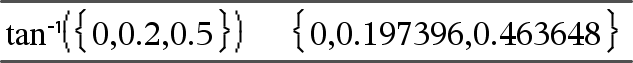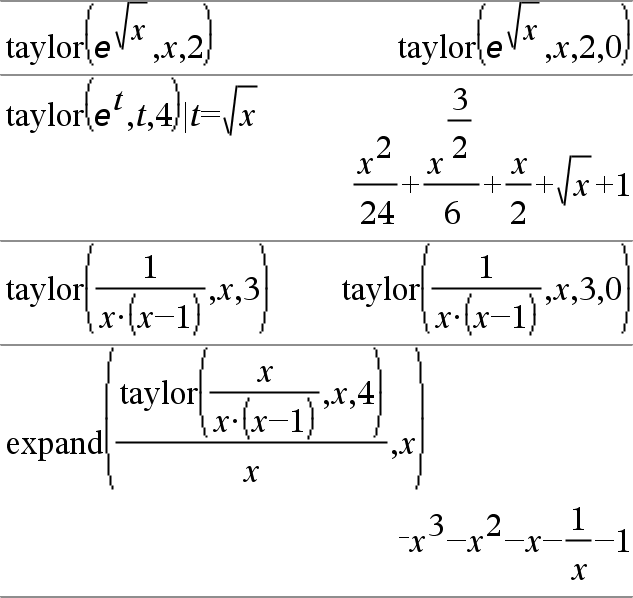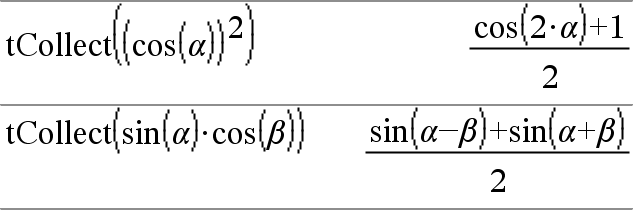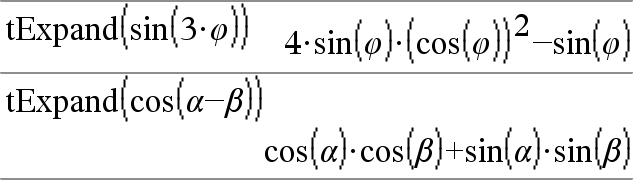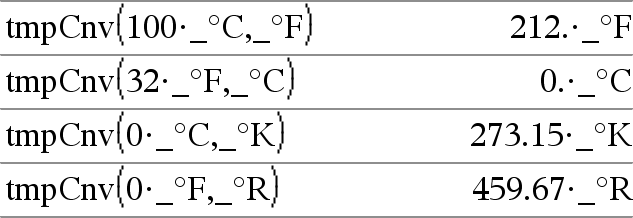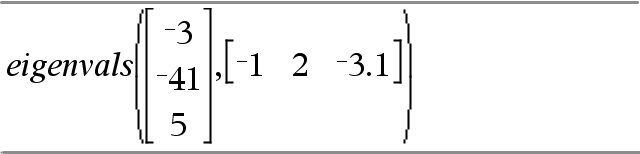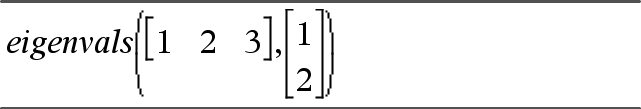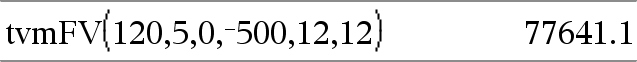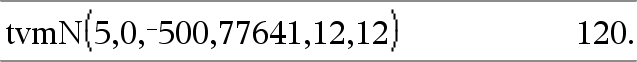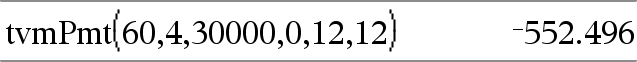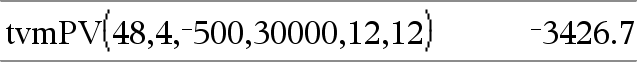|
Catalogus > |
|
|
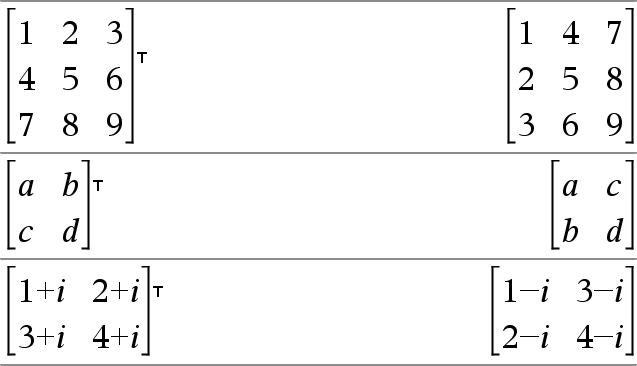
Matrix1TÞmatrix Geeft de complex geconjugeerde transponering van Matrix1. Opmerking: u kunt deze operator vanaf het toetsenbord van de computer invoeren door @t in te typen. |
|
|
µ-toets |
|
|
tan(Uitdr1)Þuitdrukking tan(Lijst1)Þlijst
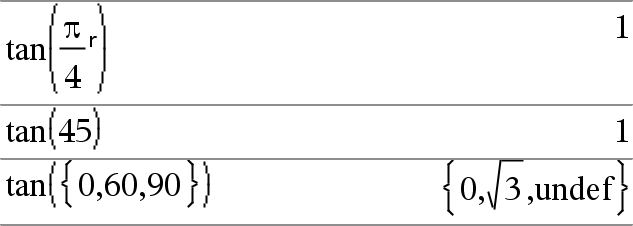
tan(Lijst1) geeft een lijst met de tangensen van alle elementen in Lijst1. Opmerking: het argument wordt geïnterpreteerd als een hoek in graden, in decimale graden of in radialen, volgens de ingestelde hoekmodus. U kunt ¡, G of Rgebruiken om de instelling van de hoekmodus tijdelijk te onderdrukken. |
In de hoekmodus Graden:
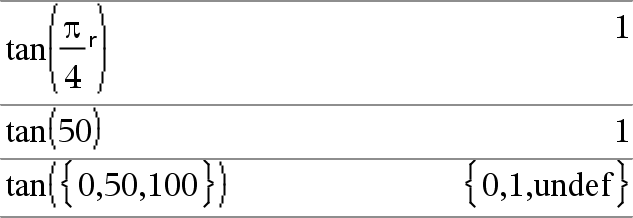
In de hoekmodus Decimale graden:
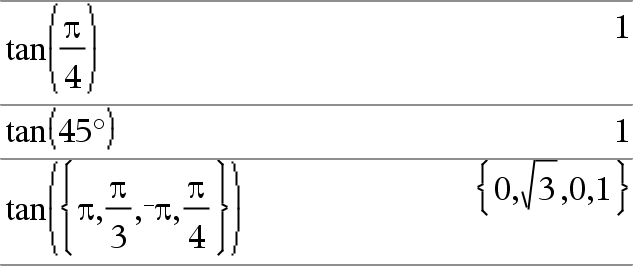
In de hoekmodus Radialen:
|
|
tan(vierkanteMatrix1)ÞvierkanteMatrix Geeft de matrixtangens van vierkanteMatrix1. Dit is niet hetzelfde als het berekenen van de tangens van elk element. Zie voor informatie over de berekeningsmethode cos(). vierkanteMatrix1 moet diagonaliseerbaar zijn. Het resultaat bevat altijd getallen met een drijvende komma. |
In de hoekmodus Radialen:
|
|
µ-toets |
|
|
tan/(Uitdr1)Þuitdrukking tan/(Lijst1)Þlijst
tan/(Lijst1) geeft een lijst met de inverse tangens van elk element in Lijst1. Opmerking: de uitkomst wordt in graden, decimale graden of radialen gegeven, volgens de ingestelde hoekmodus. Opmerking: u kunt deze operator vanaf het toetsenbord van de computer invoeren door arctan(...) in te typen. |
In de hoekmodus Graden:
In de hoekmodus Decimale graden:
In de hoekmodus Radialen:
|
|
tan/(vierkanteMatrix1)ÞvierkanteMatrix Geeft de inverse matrixtangens van vierkanteMatrix1. Dit is niet hetzelfde als het berekenen van de inverse tangens van elk element. Zie voor informatie over de berekeningsmethode cos(). vierkanteMatrix1 moet diagonaliseerbaar zijn. Het resultaat bevat altijd getallen met een drijvende komma. |
In de hoekmodus Radialen:
|
|
Catalogus > |
|
|
tangentLine(Uitdr1,Var,Punt)Þuitdrukking tangentLine(Uitdr1,Var=Punt)Þuitdrukking Geeft de raaklijn aan de kromme die gerepresenteerd wordt door Uitdr1 in het punt dat gespecificeerd is door Var=Punt. Zorg ervoor dat de onafhankelijke variabele niet gedefinieerd is. Bijvoorbeeld: als f1(x):=5 en x:=3, dan geeft tangentLine(f1(x),x,2) “false.” |
|
|
Catalogus > |
|
|
tanh(Uitdr1)Þuitdrukking tanh(Lijst1)Þlijst
tanh(Lijst1) geeft een lijst met de tangens hyperbolicus van elk element in Lijst1. |
|
|
tanh(vierkanteMatrix1)ÞvierkanteMatrix Geeft de matrixtangens hyperbolicus van vierkanteMatrix1. Dit is niet hetzelfde als het berekenen van de tangens hyperbolicus van elk element. Zie voor informatie over de berekeningsmethode cos(). vierkanteMatrix1 moet diagonaliseerbaar zijn. Het resultaat bevat altijd getallen met een drijvende komma. |
In de hoekmodus Radialen:
|
|
Catalogus > |
|
|
tanh/(Uitdr1)Þuitdrukking tanh/(Lijst1)Þlijst
tanh/(Lijst1) geeft een lijst van de inverse tangens hyperbolicus van elk element in Lijst1. Opmerking: u kunt deze operator vanaf het toetsenbord van de computer invoeren door arctanh(...) in te typen. |
In rechthoekige complexe opmaak:
|
|
tanh/(vierkanteMatrix1)ÞvierkanteMatrix Geeft de inverse matrixtangens hyperbolicus van vierkanteMatrix1. Dit is niet hetzelfde als het berekenen van de inverse tangens hyperbolicus van elk element. Zie voor informatie over de berekeningsmethode cos(). vierkanteMatrix1 moet diagonaliseerbaar zijn. Het resultaat bevat altijd getallen met een drijvende komma. |
In de hoekmodus Radialen en rechthoekige complexe opmaak:
Om het hele resultaat te zien drukt u op 5 en gebruikt u vervolgens 7 en 8 om de cursor te verplaatsen. |
|
Catalogus > |
|
|
taylor(Uitdr1, Var, Orde[, Punt])Þuitdrukking Geeft de gevraagde Taylor-polynoom. De polynoom bevat niet-nul-termen van gehele graden van nul tot Orde in (Var min Punt). taylor() geeft zichzelf terug als er geen ingekorte machtenserie van deze orde is, of als er negatieve of gebroken exponenten nodig zouden zijn. Gebruik substitutie en/of tijdelijke vermenigvuldiging met een macht van (Var min Punt) om algemenere machtenseries te bepalen. Punt heeft als standaardwaarde nul en is het uitbreidingspunt. |
|
|
Catalogus > |
|
|
tCdf(ondergrens,bovengrens,df)Þgetal als ondergrens en bovengrens getallen zijn, lijst als ondergrens en bovengrens lijsten zijn Berekent de Student-t-verdelingskans tussen ondergrens en bovengrens bij de gespecificeerde vrijheidsgraden df. Voor P(X { bovengrens) stelt u ondergrens = .ˆ. |
|
|
Catalogus > |
|
|
tCollect(Uitdr1)Þuitdrukking Geeft een uitdrukking waarin de producten en gehele machten van sinussen en cosinussen geconverteerd worden naar een lineaire combinatie van sinussen en cosinussen van meervoudige hoeken, hoeksommen en hoekverschillen. De transformatie converteert goniometrische veeltermen in een lineaire combinatie van hun harmonische elementen. Soms bereikt u met tCollect() uw doelen als dit met de standaard goniometrische vereenvoudiging niet lukt. tCollect() keert vaak transformaties die uitgevoerd zijn door tExpand() om. Soms kan het toepassen van tExpand() op een resultaat uit tCollect(), of andersom, in twee aparte stappen, een uitdrukking vereenvoudigen. |
|
|
Catalogus > |
|
|
tExpand(Uitdr1)Þuitdrukking Geeft een uitdrukking waarin sinussen en cosinussen van gehele meervoudige hoeken, hoeksommen en hoekverschillen uitgewerkt worden. Vanwege de gelijkheid (sin(x))2+(cos(x))2=1 zijn er vele equivalente resultaten mogelijk. Daarom kan een resultaat verschillen van een resultaat dat weergegeven wordt in andere publicaties. Soms bereikt u met tExpand() uw doelen als dit met de standaard goniometrische vereenvoudiging niet lukt. tExpand() keert vaak transformaties die uitgevoerd zijn door tCollect() om. Soms kan het toepassen van tCollect() op een resultaat uit tExpand(), of andersom, in twee aparte stappen, een uitdrukking vereenvoudigen. Opmerking: schaling in de graden-modus met p/180 interfereert met de mogelijkheid van tExpand() om uitwerkbare vormen te herkennen. Om de beste resultaten te krijgen moet tExpand() in de radialen-modus gebruikt worden. |
|
|
Catalogus > |
|||||||
|
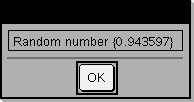
Programmeringscommando: Pauzeert het programma en geeft de tekenreeks promptString in een dialoogvenster weer. Als de gebruiker OK selecteert, gaat het programma verder. Het optionele argument vlag kan elke willekeurige uitdrukking zijn.
Als het programma een getypte respons van de gebruiker nodig heeft, zie dan Opmerking: u kunt dit commando binnen een door de gebruiker gedefinieerd programma gebruiken, maar niet binnen een functie. |
Definieer een programma dat pauzeert om vijf verschillende toevalsgetallen in een dialoogvenster weer te geven. Maak binnen de template Prgm...EndPrgm elke regel af door op @ in plaats van op · te drukken. Op het toetsenbord van de computer houdt u Alt ingedrukt en drukt u op Enter.
Define text_demo()=Prgm For i,1,5 strinfo:=”Random number “ & string(rand(i)) Text strinfo EndFor EndPrgm
Voer het programma uit: text_demo()
Voorbeeld van een dialoogvenster:
|
|
Zie If, hier. |
|
|
|
|
|
Catalogus > |
|
|
TInterval Lijst[,Freq[,CNiveau]] (Invoer van een gegevenslijst) TInterval v,Sx,n[,CNiveau] (Invoer van samenvattingsstatistieken) Berekent een t-betrouwbaarheidsinterval. Een samenvatting van de resultaten wordt opgeslagen in de variabele stat.resultaten (hier). Zie voor informatie over het effect van lege elementen in een lijst “Lege elementen” (hier). |
|
|
Uitvoervariabele |
Beschrijving |
|
stat.CLower, stat.CUpper |
Betrouwbaarheidsinterval voor een onbekend populatiegemiddelde |
|
stat.x |
Steekproefgemiddelde van de gegevensverzameling uit een normale willekeurige verdeling |
|
stat.ME |
Foutmarge |
|
stat.df |
Vrijheidsgraden |
|
stat.sx |
Standaarddeviatie steekproef |
|
stat.n |
Lengte van de gegevensverzameling met het steekproefgemiddelde |
|
Catalogus > |
|
|
tInterval_2Samp Lijst1,Lijst2[,Freq1[,Freq2[,CNiveau[,Gepoold]]]] (Invoer van een gegevenslijst) tInterval_2Samp v1,sx1,n1,v2,sx2,n2[,CNiveau[,Gepoold]] (Invoer van samenvattingsstatistieken) Berekent een t-betrouwbaarheidsinterval met twee steekproeven. Een samenvatting van de resultaten wordt opgeslagen in de variabele stat.results (hier). Gepoold=1 poolt de varianties; Gepoold=0 poolt de varianties niet. Zie voor informatie over het effect van lege elementen in een lijst “Lege elementen” (hier). |
|
|
Uitvoervariabele |
Beschrijving |
|
stat.CLower, stat.CUpper |
Betrouwbaarheidsinterval met de betrouwbaarheidskans gebaseerd op de verdeling |
|
stat.x1-x2 |
Steekproefgemiddelden van de gegevensverzameling uit de willekeurige normale verdeling |
|
stat.ME |
Foutmarge |
|
stat.df |
Vrijheidsgraden |
|
stat.x1, stat.x2 |
Steekproefgemiddelden van de gegevensverzameling uit de willekeurige normale verdeling |
|
stat.sx1, stat.sx2 |
Steekproefstandaarddeviaties voor Lijst 1 en Lijst 2 |
|
stat.n1, stat.n2 |
Aantal steekproeven in de gegevensverzamelingen |
|
stat.sp |
De gepoolde standaarddeviatie. Berekend wanneer Gepoold = JA. |
|
Catalogus > |
|
|
tmpCnv(Uitdr_¡tempEenheid, _¡tempEenheid2) Þuitdrukking _¡tempEenheid2 Converteert een temperatuurwaarde die gespecificeerd is door Uitdr van de ene eenheid naar een andere. Geldige temperatuureenheden zijn: _¡CCelsius _¡FFahrenheit _¡KKelvin _¡RRankine Om ¡ te typen selecteert u dit uit de symbolenlijst in de Catalogus. Om _ te typen drukt u op /_. Bijvoorbeeld: 100_¡C wordt geconverteerd naar 212_¡F. Om een temperatuurbereik te converteren gebruikt u @tmpCnv(). |
Opmerking: u kunt de Catalogus gebruiken om temperatuureenheden te selecteren. |
|
Catalogus > |
|
|
@tmpCnv(Uitdr_¡tempEenheid, _¡tempEenheid2) Þuitdrukking _¡tempEenheid2 Opmerking: u kunt deze operator vanaf het toetsenbord van de computer invoeren door deltaTmpCnv(...) in te typen. Converteert een temperatuurbereik (het verschil tussen twee temperatuurwaarden) dat gespecificeerd is door Uitdr van de ene eenheid naar een andere. Geldige temperatuureenheden zijn: _¡CCelsius _¡FFahrenheit _¡KKelvin _¡RRankine Om ¡ in te voeren selecteert u dit teken in het symboolpalet of typt u @d. Om _ te typen drukt u op /_. 1_¡C en 1_¡K hebben dezelfde grootte, net als 1_¡F en 1_¡R. 1_¡C is echter 9/5 maal zo groot als 1_¡F. Bijvoorbeeld: een bereik van 100_¡C (van 0_¡C tot 100_¡C) is hetzelfde als een bereik van 180_¡F. Om een bepaalde temperatuurwaarde in plaats van een bereik te converteren gebruikt u tmpCnv(). |
Om @ te typen selecteert u dit uit de symbolenlijst in de Catalogus.
Opmerking: u kunt de Catalogus gebruiken om temperatuureenheden te selecteren. |
|
Catalogus > |
|
|
tPdf(XWaarde,df)Þgetal als XWaarde een getal is, lijst als XWaarde een lijst is Berekent de kansdichtheidsfunctie (pdf) voor de Student-t-verdeling bij een gespecificeerde x-waarde met de gespecificeerde vrijheidsgraden df. |
|
|
Catalogus > |
|
|
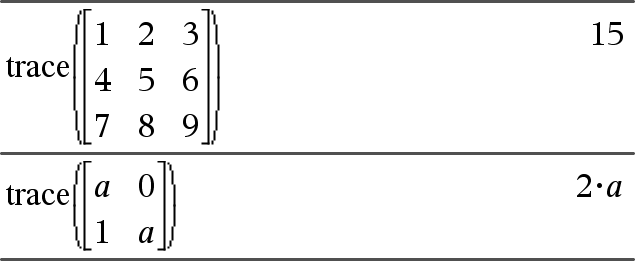
trace(vierkante matrix)Þuitdrukking Geeft het spoor (som van alle elementen van de hoofddiagonaal) van vierkanteMatrix. |
|
|
Catalogus > |
|
|
Voert blok1 uit tenzij er een fout optreedt. De uitvoering van het programma gaat over naar blok2 als er een fout optreedt in blok1. Systeemvariabele errCode bevat de foutcode zodat het programma foutherstel kan uitvoeren. Zie “Foutcodes en meldingen”, hier voor een lijst met foutcodes. blok1 en blok2 kunnen een enkele bewering of een serie beweringen zijn die gescheiden worden door het teken “:”. Opmerking bij het invoeren van het voorbeeld: Instructies over het invoeren van programma's met meerdere regels en functiedefinities vindt u in het hoofdstuk Rekenmachine van de handleiding van uw product. |
|
|
Om de commando's Try, ClrErr en PassErr in werking te zien, voert u het eigenvals() programma in dat rechts wordt weergegeven. Voer het programma uit door elk van de volgende uitdrukkingen uit te voeren.
|
Define eigenvals(a,b)=Prgm © Het programmeren van eigenvals(A,B) geeft de eigenwaarden van A·B weer Try Disp "A= ",a Disp "B= ",b Disp " " Disp "Eigenwaarden van A·B zijn:",eigVl(a*b) Else If errCode=230 Then Disp "Fout: Product van A·B moet een vierkante matrix zijn" ClrErr Else PassErr EndIf EndTry EndPrgm
|
|
Catalogus > |
|
|
tTest m0,Lijst[,Freq[,Hypoth]] (Invoer van een gegevenslijst) tTest m0,x,sx,n,[Hypoth] (Invoer van samenvattingsstatistieken) Voert een hypothesetoets uit voor één onbekend populatiegemiddelde, m, wanneer de populatiestandaarddeviate, s, onbekend is. Een samenvatting van de resultaten wordt opgeslagen in de variabele stat.results (hier). Toets H0: m = m0 tegen één van de volgende alternatieven: Voor H1: m < m0 stelt u Hypoth<0 in Voor H1: m ƒ m0 (standaardinstelling) stelt u Hypoth=0 in Voor H1: m > m0 stelt u Hypoth>0 in Zie voor informatie over het effect van lege elementen in een lijst “Lege elementen” (hier). |
|
|
Uitvoervariabele |
Beschrijving |
|
stat.t |
(x N m0) / (stdev / sqrt(n)) |
|
stat.PVal |
Kleinste significantieniveau waarbij de nulhypothese verworpen kan worden |
|
stat.df |
Vrijheidsgraden |
|
stat.x |
Steekproefgemiddelde van de gegevensverzameling in Lijst |
|
stat.sx |
Steekproefstandaarddeviatie van de gegevensverzameling |
|
stat.n |
Omvang van de steekproef |
|
Catalogus > |
|
|
tTest_2Samp Lijst1,Lijst2[,Freq1[,Freq2[,Hypoth[,Gepoold]]]] (Invoer van een gegevenslijst) tTest_2Samp v1,sx1,n1,v2,sx2,n2[,Hypoth[,Gepoold]] (Invoer van samenvattingsstatistieken) Berekent een t-toets met twee steekproeven. Een samenvatting van de resultaten wordt opgeslagen in de variabele stat.results (hier). Toets H0: m1 = m2 tegen een van de volgende alternatieven: Voor H1: m1< m2 stelt u Hypoth<0 in Voor H1: m1ƒ m2 (standaardinstelling) stelt u Hypoth=0 in Voor H1: m1> m2 stelt u Hypoth>0 in Gepoold=1 poolt de varianties Gepoold=0 poolt de varianties niet Zie voor informatie over het effect van lege elementen in een lijst “Lege elementen” (hier). |
|
Uitvoervariabele |
Beschrijving |
|
stat.t |
Standaard normale waarde berekend voor het verschil tussen de gemiddelden |
|
stat.PVal |
Kleinste significantieniveau waarbij de nulhypothese verworpen kan worden |
|
stat.df |
Vrijheidsgraden voor de t-statistiek |
|
stat.x1, stat.x2 |
Steekproefgemiddelden van de gegevensverzamelingen in Lijst 1 en Lijst 2 |
|
stat.sx1, stat.sx2 |
Steekproefstandaarddeviaties van de gegevensverzamelingen in Lijst 1 en Lijst 2 |
|
stat.n1, stat.n2 |
Grootte van de steekproeven |
|
stat.sp |
De gepoolde standaarddeviatie. Berekend wanneer Gepoold=1. |
|
Catalogus > |
|
|
tvmFV(N,I,PV,Pmt,[PpY],[CpY],[PmtAt])Þwaarde Financiële functie die de toekomstige waarde van geld berekent. Opmerking: de argumenten die in de TVM-functies worden gebruikt, worden beschreven in de tabel met TVM-argumenten, hier. Zie ook amortTbl(), hier. |
|
|
Catalogus > |
|
|
tvmI(N,PV,Pmt,FV,[PpY],[CpY],[PmtAt])Þwaarde Financiële functie die het rentepercentage per jaar berekent. Opmerking: de argumenten die in de TVM-functies worden gebruikt, worden beschreven in de tabel met TVM-argumenten, hier. Zie ook amortTbl(), hier. |
|
|
Catalogus > |
|
|
tvmN(I,PV,Pmt,FV,[PpY],[CpY],[PmtAt])Þwaarde Financiële functie die het aantal betalingsperioden berekent. Opmerking: de argumenten die in de TVM-functies worden gebruikt, worden beschreven in de tabel met TVM-argumenten, hier. Zie ook amortTbl(), hier. |
|
|
Catalogus > |
|
|
tvmPmt(N,I,PV,FV,[PpY],[CpY],[PmtAt])Þwaarde Financiële functie die het bedrag van elke betaling berekent. Opmerking: de argumenten die in de TVM-functies worden gebruikt, worden beschreven in de tabel met TVM-argumenten, hier. Zie ook amortTbl(), hier. |
|
|
Catalogus > |
|
|
tvmPV(N,I,Pmt,FV,[PpY],[CpY],[PmtAt])Þwaarde Financiële functie die de contante waarde berekent. Opmerking: de argumenten die in de TVM-functies worden gebruikt, worden beschreven in de tabel met TVM-argumenten, hier. Zie ook amortTbl(), hier. |
|
|
Beschrijving |
Gegevenstype |
|
|
N |
Aantal betalingsperioden |
reëel getal |
|
I |
Rentepercentage per jaar |
reëel getal |
|
PV |
Contante waarde |
reëel getal |
|
Pmt |
Betalingsbedrag |
reëel getal |
|
FV |
Toekomstige waarde |
reëel getal |
|
PpY |
Betalingen per jaar, standaardinstelling=1 |
geheel getal > 0 |
|
CpY |
Rentetermijnen per jaar, standaardinstelling=1 |
geheel getal > 0 |
|
PmtAt |
Betaling vindt plaats aan het begin of op het eind van elke periode, standaardinstelling=eind |
geheel getal (0=einde, 1=begin) |
* Deze tijdwaarde-van-geld-argumentnamen zijn gelijk aan de TVM-variabelenamen (zoals tvm.pv en tvm.pmt) die gebruikt worden door de financiële oplosser van de Rekenmachine.Financiële functies slaan hun argumentwaarden of resultaten echter niet op naar de TVM-variabelen.
|
Catalogus > |
|
|
TwoVar X, Y[, [Freq] [, Categorie, Opnemen]] Berekent de statistieken voor twee variabelen. Een samenvatting van de resultaten wordt opgeslagen in de variabele stat.resultaten (hier). Alle lijsten moeten gelijke afmetingen hebben, behalve Opnemen. X en Y zijn lijsten met onafhankelijke en afhankelijke variabelen. Freq is een optionele lijst met frequentiewaarden. Elk element in Freq specificeert de frequentie waarmee elk overeenkomstig X- en Y-gegeven voorkomt. De standaardwaarde is 1. Alle elementen moeten gehele getallen | 0 zijn. Categorie is een lijst met categoriecodes voor de overeenkomstige X- en Y-gegevens.. Opnemen is een lijst met één of meer van de categoriecodes. Alleen de gegevens waarvan de categoriecode is opgenomen in deze lijst worden opgenomen in de berekening. Een leeg element in een van de lijsten X, Freq of Categorie resulteert in een lege plaats voor het overeenkomstige element in al deze lijsten. Een leeg element in een van de lijsten X1 tot en met X20 resulteert in een lege plaats voor het overeenkomstige element in al deze lijsten. Voor meer informatie over lege elementen, zie hier. |
|
|
Uitvoervariabele |
Beschrijving |
|
stat.v |
Gemiddelde van de x-waarden |
|
stat.Gx |
Som van de x-waarden |
|
stat.Gx2 |
Som van de x2-waarden |
|
stat.sx |
Steekproef-standaarddeviatie van x |
|
stat.sx |
Populatie-standaarddeviatie van x |
|
stat.n |
Aantal gegevens |
|
stat.w |
Gemiddelde van y-waarden |
|
stat.Gy |
Som van de y-waarden |
|
stat.Gy2 |
Som van de y2-waarden |
|
stat.sy |
Steekproefstandaarddeviatie van y |
|
stat.sy |
Populatiestandaarddeviatie van y |
|
stat.Gxy |
Som van de x·y-waarden |
|
stat.r |
Correlatiecoëfficiënt |
|
stat.MinX |
Minimum van de x-waarden |
|
stat.Q1X |
1ste kwartiel van x |
|
stat.MedianX |
Mediaan van x |
|
stat.Q3X |
3de kwartiel van x |
|
stat.MaxX |
Maximum van de x-waarden |
|
stat.MinY |
Minimum van de y-waarden |
|
stat.Q1Y |
1ste kwartiel van y |
|
stat.MedY |
Mediaan van y |
|
stat.Q3Y |
3de kwartiel van y |
|
stat.MaxY |
Maximum van y-waarden |
|
stat.G(x-v)2 |
Som van de kwadraten van de afwijkingen ten opzichte van het gemiddelde van x |
|
stat.G(y-w)2 |
Som van de kwadraten van afwijkingen ten opzichte van het gemiddelde van y |