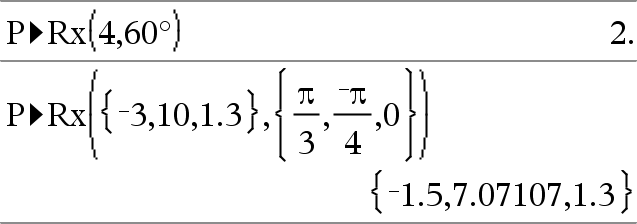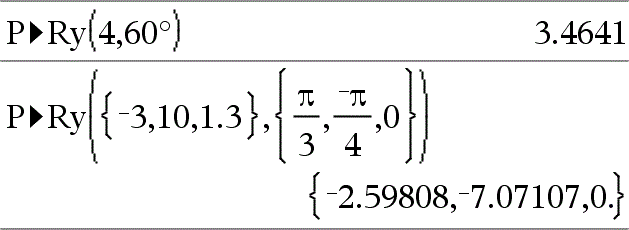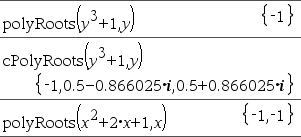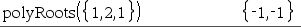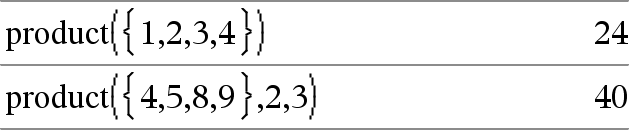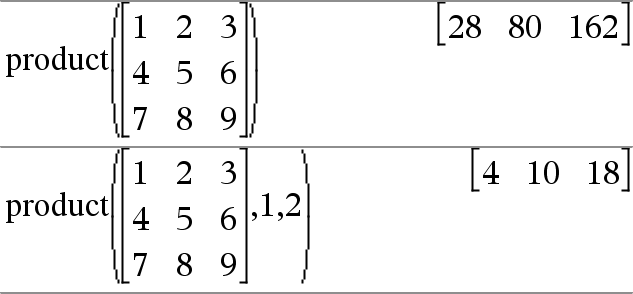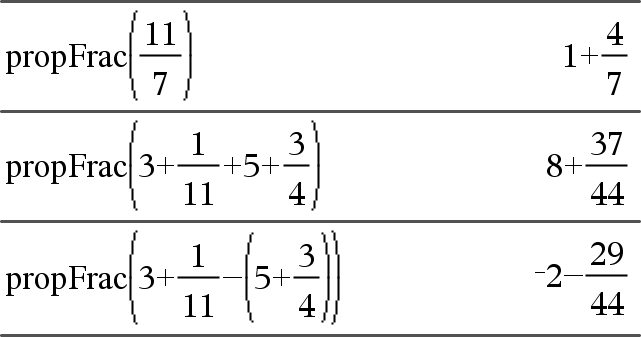|
Catalogue > |
|
|
P4Rx(ExprR, qExpr)Þexpression P4Rx(ListeR, qListe)Þliste P4Rx(MatriceR, qMatrice)Þmatrice Donne la valeur de l'abcisse du point de coordonnées polaires (r, q). Remarque : l'argument q est interprété comme une mesure en degrés, en grades ou en radians, suivant le mode Angle utilisé. Si l'argument est une expression, vous pouvez utiliser ¡, G ou Rpour ignorer temporairement le mode Angle sélectionné. Remarque : vous pouvez insérer cette fonction à partir du clavier de l'ordinateur en entrant P@>Rx(...). |
En mode Angle en radians :
|
|
Catalogue > |
|
|
P4Ry(ValeurR, qValeur)Þvaleur P4Ry(ListeR, qListe)Þliste P4Ry(MatriceR, qMatrice)Þmatrice Donne la valeur de l'ordonnée du point de coordonnées polaires (r, q). Remarque : l'argument q est interprété comme une mesure en degrés, en grades ou en radians, suivant le mode Angle utilisé. Remarque : vous pouvez insérer cette fonction à partir du clavier de l'ordinateur en entrant P@>Ry(...). |
En mode Angle en radians :
|
|
Catalogue > |
|
|
PassErr Passe une erreur au niveau suivant. Si la variable système errCode est zéro, PassErr ne fait rien. L'instruction Else du bloc Try...Else...EndTry doit utiliser EffErr ou PassErr. Si vous comptez rectifier ou ignorer l'erreur, sélectionnez EffErr. Si vous ne savez pas comment traiter l'erreur, sélectionnez PassErr pour la transférer au niveau suivant. S'il n'y a plus d'autre programme de traitement des erreurs Try...Else...EndTry, la boîte de dialogue Erreur s'affiche normalement. Remarque : Voir aussi ClrErr, ici et Try, ici. Remarque pour la saisie des données de l’exemple : Pour obtenir des instructions sur la saisie des définitions de fonction ou de programme sur plusieurs lignes, consultez la section relative à la calculatrice dans votre guide de produit. |
Pour obtenir un exemple de PassErr, reportez-vous à l'exemple 2 de la commande Try, ici. |
|
Catalogue > |
|
|
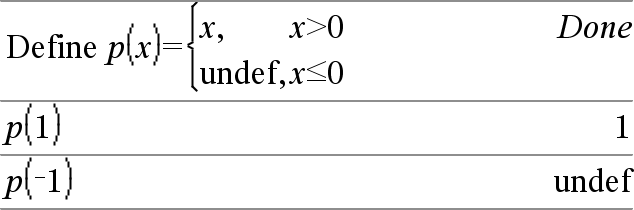
piecewise(Expr1 [, Condition1 [, Expr2 [, Condition2 [, … ]]]]) Permet de créer des fonctions définies par morceaux sous forme de liste. Il est également possible de créer des fonctions définies par morceaux en utilisant un modèle. Remarque : voir aussi Modèle Fonction définie par morceaux, ici. |
|
|
Catalogue > |
|
|
poissCdf(l,lowBound,upBound)Þnombre si lowBound et upBound sont des nombres, liste si lowBound et upBound sont des listes poissCdf(l,upBound)(pour P(0{X{upBound)Þnombre si la borne upBound est un nombre, liste si la borne upBound est une liste Calcule la probabilité cumulée d'une variable suivant une loi de Poisson de moyenne l. Pour P(X { upBound), définissez la borne lowBound=0 |
|
|
Catalogue > |
|
|
poissPdf(l,ValX)Þnombre si ValX est un nombre, liste si ValX est une liste Calcule la probabilité de ValX pour la loi de Poisson de moyenne l spécifiée. |
|
|
Catalogue > |
|||||||
|
Vecteur 4Polar Remarque : vous pouvez insérer cet opérateur à partir du clavier de l'ordinateur en entrant @>Polar. Affiche vecteur sous forme polaire [r∠θ]. Le vecteur doit être un vecteur ligne ou colonne et de dimension 2. Remarque : 4Polar est uniquement une instruction d'affichage et non une fonction de conversion. On ne peut l'utiliser qu'à la fin d'une ligne et elle ne modifie pas le contenu du registre ans. Remarque : voir aussi 4Rect, ici. |
|
||||||
|
valeurComplexe 4Polar Affiche valeurComplexe sous forme polaire.
valeurComplexe peut prendre n'importe quelle forme complexe. Toutefois, une entrée reiθ génère une erreur en mode Angle en degrés. Remarque : vous devez utiliser les parenthèses pour les entrées polaires (r∠θ). |
En mode Angle en radians :
En mode Angle en grades :
En mode Angle en degrés :
|
|
Catalogue > |
|
|
polyEval(Liste1, Expr1)Þexpression polyEval(Liste1, Liste2)Þexpression Interprète le premier argument comme les coefficients d'un polynôme ordonné suivant les puissances décroissantes et calcule la valeur de ce polynôme au point indiqué par le deuxième argument. |
|
|
Catalogue > |
|
|
La première syntaxe, La deuxième syntaxe, Remarque : voir aussi |
|
|
Catalogue > |
|
|
PowerReg X,Y [, Fréq] [, Catégorie, Inclure]] Effectue l'ajustement exponentiely = (a·(x)b)sur les listes X et Y en utilisant la fréquence Fréq. Un récapitulatif du résultat est stocké dans la variable stat.results. (Voir ici.) Toutes les listes doivent comporter le même nombre de lignes, à l'exception de Inclure. X et Y sont des listes de variables indépendantes et dépendantes. Fréq est une liste facultative de valeurs qui indiquent la fréquence. Chaque élément dans Fréq correspond à une fréquence d'occurrence pour chaque couple X et Y. Par défaut, cette valeur est égale à 1. Tous les éléments doivent être des entiers | 0. Catégorie est une liste de codes Inclure est une liste d'un ou plusieurs codes de catégories. Seuls les éléments dont le code de catégorie figure dans cette liste sont inclus dans le calcul. Pour plus d'informations concernant les éléments vides dans une liste, reportez-vous à “Éléments vides”, ici. |
|
|
Variable de sortie |
Description |
|
stat.RegEqn |
Équation d'ajustement : a·(x)b |
|
stat.a, stat.b |
Coefficients d'ajustement |
|
stat.r2 |
Coefficient de détermination linéaire pour les données transformées |
|
stat.r |
Coefficient de corrélation pour les données transformées (ln(x), ln(y)) |
|
stat.Resid |
Valeurs résiduelles associées au modèle exponentiel |
|
stat.ResidTrans |
Valeurs résiduelles associées à l'ajustement linéaire des données transformées |
|
stat.XReg |
Liste des points de données de la liste Liste X modifiée, actuellement utilisée dans l'ajustement basé sur les restrictions de Fréq, Liste de catégories et Inclure les catégories |
|
stat.YReg |
Liste des points de données de la liste Liste Y modifiée, actuellement utilisée dans l'ajustement basé sur les restrictions de Fréq, Liste de catégories et Inclure les catégories |
|
stat.FreqReg |
Liste des fréquences correspondant à stat.XReg et stat.YReg |
|
Catalogue > |
|
|
Prgm Modèle de création d'un programme défini par l'utilisateur. À utiliser avec la commande Define, Define LibPub, ou Define LibPriv. Bloc peut correspondre à une instruction unique ou à une série d'instructions séparées par le caractère “:” ou à une série d'instructions réparties sur plusieurs lignes. Remarque pour la saisie des données de l’exemple : Pour obtenir des instructions sur la saisie des définitions de fonction ou de programme sur plusieurs lignes, consultez la section relative à la calculatrice dans votre guide de produit. |
Calcule le plus grand commun diviseur et affiche les résultats intermédiaires.
|
|
Voir P(), ici. |
|
|
|
|
|
Voir P(), ici. |
|
|
|
|
|
Catalogue > |
|
|
product(Liste[, Début[, Fin]])Þexpression Donne le produit des éléments de Liste. Début et Fin sont facultatifs. Ils permettent de spécifier une plage d'éléments. |
|
|
product(Matrice1[, Début[, Fin]])Þmatrice Donne un vecteur ligne contenant les produits des éléments ligne par ligne de Matrice1. Début et Fin sont facultatifs. Ils permettent de spécifier une plage de colonnes. Les éléments vides sont ignorés. Pour plus d'informations concernant les éléments vides, reportez-vous à la ici. |
|
|
Catalogue > |
|
|
propFrac(Valeur1[, Var])Þvaleur propFrac(nombre_rationnel) décompose nombre_rationnel sous la forme de la somme d'un entier et d'une fraction de même signe et dont le dénominateur est supérieur au numérateur (fraction propre). |
|
|
propFrac(expression_rationnelle,Var) donne la somme des fractions propres et d'un polynôme par rapport à Var. Le degré de Var dans le dénominateur est supérieur au degré de Var dans le numérateur pour chaque fraction propre. Les mêmes puissances de Var sont regroupées. Les termes et leurs facteurs sont triés, Var étant la variable principale. Si Var est omis, le développement des fractions propres s'effectue par rapport à la variable la plus importante. Les coefficients de la partie polynomiale sont ensuite ramenés à leur forme propre par rapport à leur variable la plus importante, et ainsi de suite. |
|
|
Vous pouvez utiliser la fonction propFrac() pour représenter des fractions mixtes et démontrer l'addition et la soustraction de fractions mixtes. |
|