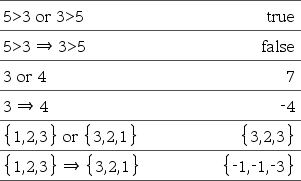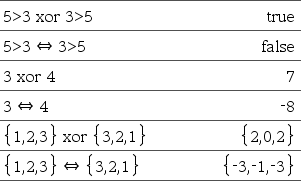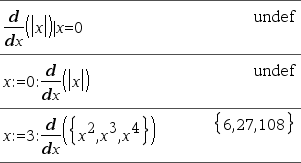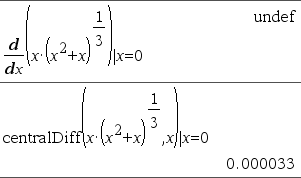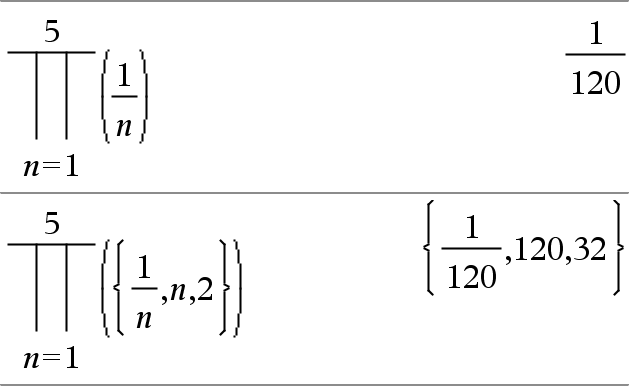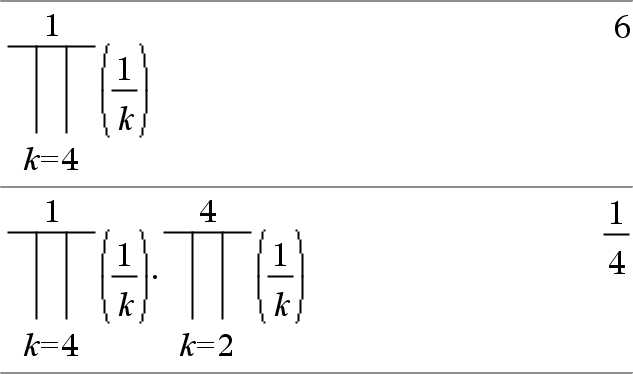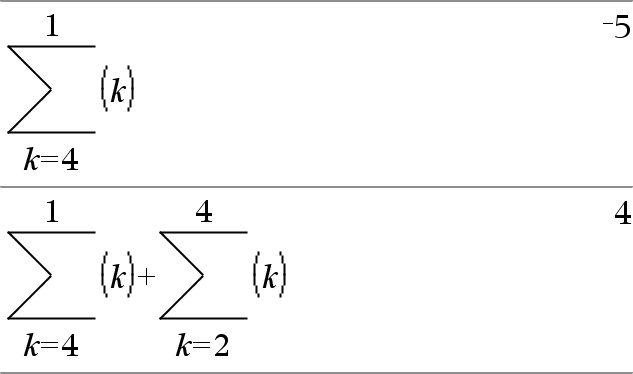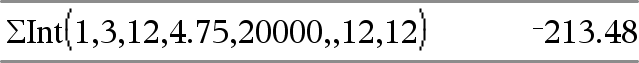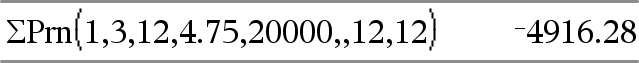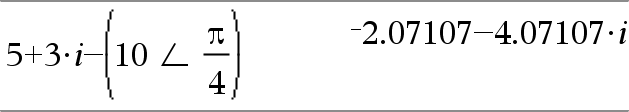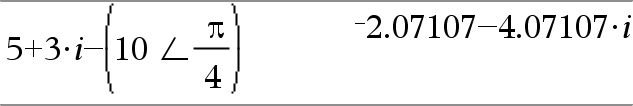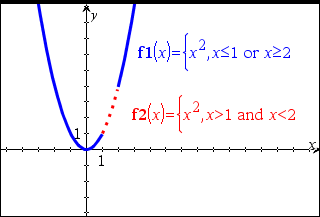|
Touche + |
|
|
Donne la somme des deux arguments. |
|
|
Liste1 + Liste2Þliste Matrice1 + Matrice2Þmatrice Donne la liste (ou la matrice) contenant les sommes des éléments correspondants de Liste1 et Liste2 (ou Matrice1 et Matrice2). Les arguments doivent être de même dimension. |
|
|
Liste1 + ValeurÞliste
|
|
|
Matrice1 + ValeurÞmatrice Donne la matrice obtenue en ajoutant Valeur à chaque élément de la diagonale de Matrice1. Matrice1 doit être carrée. Remarque : utilisez .+ pour ajouter une expression à chaque élément de la matrice. |
|
|
Touche - |
|
|
|
|
|
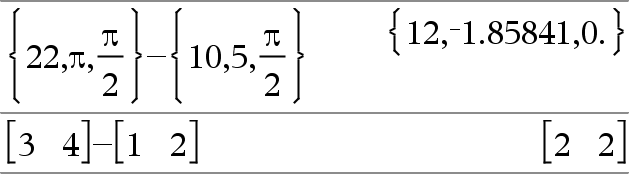
Liste1 N Liste2Þliste Matrice1 N Matrice2Þmatrice Soustrait chaque élément de Liste2 (ou Matrice2) de l'élément correspondant de Liste1 (ou Matrice1) et donne le résultat obtenu. Les arguments doivent être de même dimension. |
|
|
Liste1 N ValeurÞliste
|
|
|
Matrice1 N ValeurÞmatrice Valeur N Matrice1 donne la matrice Valeur fois la matrice d'identité moins Matrice1. Matrice1 doit être carrée. Matrice1 N Valeur donne la matrice obtenue en soustrayant Valeur à chaque élément de la diagonale de Matrice1. Matrice1 doit être carrée. Remarque : Utilisez .N pour soustraire une expression à chaque élément de la matrice. |
|
|
Touche r |
|
|
Donne le produit des deux arguments. |
|
|
Liste1·Liste2Þliste Donne la liste contenant les produits des éléments correspondants de Liste1 et Liste2. Les listes doivent être de même dimension. |
|
|
Matrice1 ·Matrice2Þmatrice Donne le produit des matrices Matrice1 et Matrice2. Le nombre de colonnes de Matrice1 doit être égal au nombre de lignes de Matrice2. |
|
|
Liste1 ·ValeurÞliste
|
|
|
Matrice1 ·ValeurÞmatrice Donne la matrice contenant les produits de Valeur et de chaque élément de Matrice1. Remarque : Utilisez .·pour multiplier une expression par chaque élément. |
|
|
Touche p |
|
|
Donne le quotient de Valeur1 par Valeur2. Remarque : voir aussi Modèle Fraction, ici. |
|
|
Liste1 à Liste2Þliste Donne la liste contenant les quotients de Liste1 par Liste2. Les listes doivent être de même dimension. |
|
|
Liste1 à Valeur Þ liste
|
|
|
Donne la matrice contenant les quotients des éléments de Matrice1àValeur. Remarque : Utilisez . / pour diviser une expression par chaque élément. |
|
|
Touche l |
|
|
Liste1 ^ Liste2 Þ liste Donne le premier argument élevé à la puissance du deuxième argument. Remarque : voir aussi Modèle Exposant, ici. Dans le cas d'une liste, donne la liste des éléments de Liste1 élevés à la puissance des éléments correspondants de Liste2. Dans le domaine réel, les puissances fractionnaires possédant des exposants réduits avec des dénominateurs impairs utilise la branche réelle, tandis que le mode complexe utilise la branche principale. |
|
|
|
|
|
|
|
|
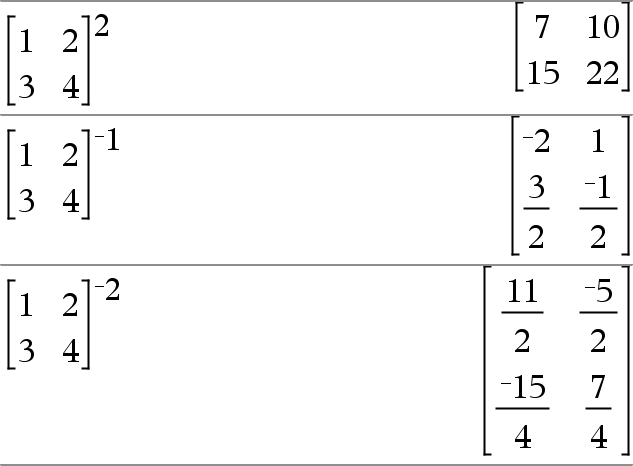
matriceCarrée1 ^ entier Þ matrice Donne matriceCarrée1 élevée à la puissance de la valeur de l'entier. matriceCarrée1 doit être une matrice carrée. Si entier = L1, calcule la matrice inverse. Si entier < L1, calcule la matrice inverse à une puissance positive appropriée. |
|
|
Touche q |
|
|
Donne le carré de l'argument. Liste12 Þ liste Donne la liste comportant les carrés des éléments de Liste1. matriceCarrée1 2Þ matrice Donne le carré de la matrice matriceCarrée1. Ce calcul est différent du calcul du carré de chaque élément. Utilisez .^2 pour calculer le carré de chaque élément. |
|
|
Touches ^+ |
|
|
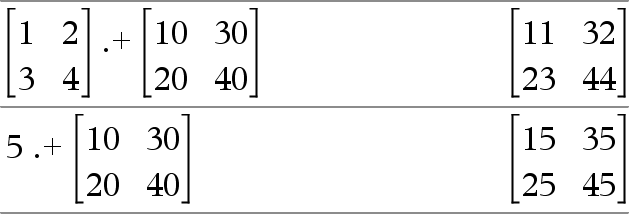
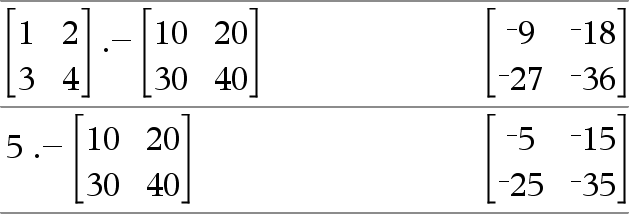
Matrice1 .+ Matrice2 Þ matrice Matrice1 .+ Matrice2 donne la matrice obtenue en effectuant la somme de chaque paire d'éléments correspondants de Matrice1 et de Matrice2.
|
|
|
Touches ^- |
|
|
Matrice1 .N Matrice2 Þ matrice Matrice1 .NMatrice2 donne la matrice obtenue en calculant la différence entre chaque paire d'éléments correspondants de Matrice1 et de Matrice2.
|
|
|
Touches ^r |
|
|
Matrice1 .· Matrice2 Þ matrice Matrice1 .· Matrice2 donne la matrice obtenue en calculant le produit de chaque paire d'éléments correspondants de Matrice1 et de Matrice2.
|
|
|
Touches ^p |
|
|
Matrice1 . / Matrice2 Þ matrice Matrice1 ./ Matrice2 donne la matrice obtenue en calculant le quotient de chaque paire d'éléments correspondants de Matrice1 et de Matrice2.
|
|
|
Touches ^l |
|
|
Matrice1 .^ Matrice2 Þ matrice Matrice1 .^ Matrice2 donne la matrice obtenue en élevant chaque élément de Matrice1 à la puissance de l'élément correspondant de Matrice2.
|
|
|
Touche v |
|
|
LListe1 Þ liste LMatrice1 Þ matrice Donne l'opposé de l'argument. Dans le cas d'une liste ou d'une matrice, donne l'opposé de chacun des éléments. Si l'argument est un entier binaire ou hexadécimal, la négation donne le complément à deux. |
En mode base Bin : Important : utilisez le chiffre zéro et pas la lettre O.
Pour afficher le résultat entier, appuyez sur 5, puis utilisez les touches 7 et 8 pour déplacer le curseur. |
|
Touches /k |
|
|
Liste1 % Þ liste Matrice1 % Þ matrice Donne Dans le cas d'une liste ou d'une matrice, donne la liste ou la matrice obtenue en divisant chaque élément par 100. |
Remarque: Pour afficher un résultat approximatif, Unité : Appuyez sur / ·.
|
|
Touche = |
|
|
Expr1 = Expr2ÞExpression booléenne Liste1 = Liste2Þ Liste booléenne Matrice1 = Matrice2Þ Matrice booléenne Donne true s'il est possible de vérifier que la valeur de Expr1 est égale à celle de Expr2. Donne false s'il est possible de déterminer que la valeur de Expr1 n'est pas égale à celle de Expr2. Dans les autres cas, donne une forme simplifiée de l'équation. Dans le cas d'une liste ou d'une matrice, donne le résultat des comparaisons, élément par élément. Remarque pour la saisie des données de l’exemple : Pour obtenir des instructions sur la saisie des définitions de fonction ou de programme sur plusieurs lignes, consultez la section relative à la calculatrice dans votre guide de produit. |
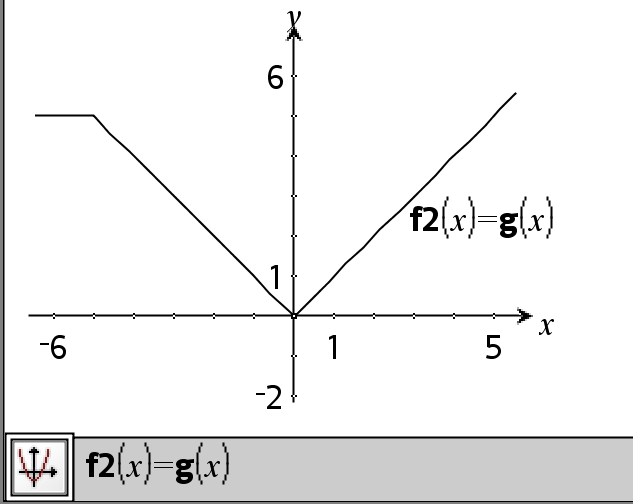
Exemple de fonction qui utilise les symboles de test mathématiques : =, ƒ, <, {, >, |
Résultat de la représentation graphique de g(x)
|
|
Touches /= |
|
|
Expr1 ƒ Expr2 Þ Expression booléenne Liste1 ƒ Liste2 Þ Liste booléenne Matrice1 ƒ Matrice2 Þ Matrice booléenne Donne true s'il est possible de déterminer que la valeur de Expr1 n'est pas égale à celle de Expr2. Donne false s'il est possible de vérifier que la valeur de Expr1 est égale à celle de Expr2. Dans les autres cas, donne une forme simplifiée de l'équation. Dans le cas d'une liste ou d'une matrice, donne le résultat des comparaisons, élément par élément. Remarque : vous pouvez insérer cet opérateur à partir du clavier de l'ordinateur en entrant /= |
Voir l'exemple fourni pour « = » (égal à). |
|
Touches /= |
|
|
Expr1 < Expr2 Þ Expression booléenne Liste1 < Liste2 Þ Liste booléenne Matrice1 < Matrice2 Þ Matrice booléenne Donne true s'il est possible de déterminer que la valeur de Expr1 est strictement inférieure à celle de Expr2. Donne false s'il est possible de déterminer que la valeur de Expr1 est strictement supérieure ou égale à celle de Expr2. Dans les autres cas, donne une forme simplifiée de l'équation. Dans le cas d'une liste ou d'une matrice, donne le résultat des comparaisons, élément par élément. |
Voir l'exemple fourni pour « = » (égal à). |
|
Touches /= |
|
|
Expr1 { Expr2 Þ Expression booléenne Liste1 { Liste2 Þ Liste booléenne Matrice1 { Matrice2 Þ Matrice booléenne Donne true s'il est possible de déterminer que la valeur de Expr1 est inférieure ou égale à celle de Expr2. Donne false s'il est possible de déterminer que la valeur de Expr1 est strictement supérieure à celle de Expr2. Dans les autres cas, donne une forme simplifiée de l'équation. Dans le cas d'une liste ou d'une matrice, donne le résultat des comparaisons, élément par élément. Remarque : vous pouvez insérer cet opérateur à partir du clavier de l'ordinateur en entrant <= |
Voir l'exemple fourni pour « = » (égal à). |
|
Touches /= |
|
|
Expr1 > Expr2 Þ Expression booléenne Liste1 > Liste2 Þ Liste booléenne Matrice1 > Matrice2 Þ Matrice booléenne Donne true s'il est possible de déterminer que la valeur de Expr1 est supérieure à celle de Expr2. Donne false s'il est possible de déterminer que la valeur de Expr1 est strictement inférieure ou égale à celle de Expr2. Dans les autres cas, donne une forme simplifiée de l'équation. Dans le cas d'une liste ou d'une matrice, donne le résultat des comparaisons, élément par élément. |
Voir l'exemple fourni pour « = » (égal à). |
|
Touches /= |
|
|
Expr1 | Expr2 Þ Expression booléenne Liste1 | Liste2 Þ Liste booléenne Matrice1 | Matrice2 Þ Matrice booléenne Donne true s'il est possible de déterminer que la valeur de Expr1 est supérieure ou égale à celle de Expr2. Donne false s'il est possible de déterminer que la valeur de Expr1 est inférieure ou égale à celle de Expr2. Dans les autres cas, donne une forme simplifiée de l'équation. Dans le cas d'une liste ou d'une matrice, donne le résultat des comparaisons, élément par élément. Remarque : vous pouvez insérer cet opérateur à partir du clavier de l'ordinateur en entrant >= |
Voir l'exemple fourni pour « = » (égal à). |
|
touches /= |
|
|
BooleanExpr1 Þ BooleanExpr2 renvoie expression booléenne BooleanList1 Þ BooleanList2 renvoie liste booléenne BooleanMatrix1 Þ BooleanMatrix2 renvoie matrice booléenne Integer1 Þ Integer2 renvoie entier
Évalue l'expression Pour les listes et matrices, renvoie le résultat des comparaisons, élément par élément. Remarque : Vous pouvez insérer cet opérateur à partir du clavier de l'ordinateur en entrant => |
|
|
touches /= |
|
|
BooleanExpr1 Û BooleanExpr2 renvoie expression booléenne BooleanList1 Û BooleanList2 renvoie liste booléenne BooleanMatrix1 Û BooleanMatrix2 renvoie matrice booléenne Integer1 Û Integer2 renvoie entier
Renvoie la négation d'une opération booléenne Pour les listes et matrices, renvoie le résultat des comparaisons, élément par élément. Remarque : Vous pouvez insérer cet opérateur à partir du clavier de l'ordinateur en entrant <=> |
|
|
Touche º |
|
|
Valeur1! Þ valeur Liste1! Þ liste Matrice1! Þ matrice Donne la factorielle de l'argument. Dans le cas d'une liste ou d'une matrice, donne la liste ou la matrice des factorielles de tous les éléments. |
|
|
Touches /k |
|
|
Chaîne1 & Chaîne2 Þ chaîne Donne une chaîne de caractères obtenue en ajoutant Chaîne2 à Chaîne1. |
|
|
Catalogue > |
|
|
d(Expr1, Var[, Ordre]) | Var=ValeurÞvaleur d(Expr1, Var[, Ordre])Þvaleur d(Liste1, Var[, Ordre])Þliste d(Matrice1, Var[, Ordre])Þmatrice Excepté si vous utilisez la première syntaxe, vous devez stocker une valeur numérique dans la variable Var avant de calculer d(). Reportez-vous aux exemples.
Order, si utilisé, doit avoir la valeur 1 ou 2. La valeur par défaut est 1. Remarque : vous pouvez insérer cette fonction à partir du clavier en entrant ""
|
|
|
Observez l'exemple ci-contre. La dérivée première de x·(x^2+x)^(1/3) en x=0 est égale à 0. Toutefois, comme la dérivée première de la sous-expression (x^2+x)^(1/3) n'est pas définie à x=0 et que cette valeur est utilisée pour calculer la dérivée de l'expression complète, d() signale que le résultat n'est pas défini et affiche un message d'avertissement.
|
|
|
Catalogue > |
|
|
‰(Expr1, Var, Borne1, Borne2) Þ valeur Affiche l'intégrale de Expr1 pour la variable Var entre Borne1 et Borne2. Vous pouvez l'utiliser pour calculer l'intégrale définie numérique en utilisant la même méthode qu'avec nInt(). Remarque : vous pouvez insérer cette fonction à partir du clavier en entrant integral(...). Remarque : voir aussi nInt(), ici et le modèle Intégrale définie, ici. |
|
|
Touches /q |
|
|
‡ (Liste1)Þliste Donne la racine carrée de l'argument. Dans le cas d'une liste, donne la liste des racines carrées des éléments de Liste1. Remarque : vous pouvez insérer cette fonction à partir du clavier en entrant sqrt(...) Remarque : voir aussi Modèle Racine carrée, ici. |
|
|
Catalogue > |
|
|
P(Expr1, Var, Début, Fin)Þexpression Remarque : vous pouvez insérer cette fonction à partir du clavier en entrant prodSeq(...). Calcule Expr1 pour chaque valeur de Var comprise entre Début et Fin et donne le produit des résultats obtenus. Remarque : voir aussi Modèle Produit (P), ici. |
|
|
P(Expr1, Var, Début, DébutN1)Þ1 P(Expr1, Var, Début, Fin) Þ1/P(Expr1, Var, Fin+1, DébutN1) if Début < FinN1 Les formules de produit utilisées sont extraites des références ci-dessous : Ronald L. Graham, Donald E. Knuth et Oren Patashnik. Concrete Mathematics: A Foundation for Computer Science. Reading, Massachusetts: Addison-Wesley, 1994. |
|
|
Catalogue > |
|
|
G(Expr1, Var, Début, Fin)Þexpression Remarque : vous pouvez insérer cette fonction à partir du clavier en entrant sumSeq(...). Calcule Expr1 pour chaque valeur de Var comprise entre Début et Fin et donne la somme des résultats obtenus. Remarque : voir aussi Modèle Somme, ici. |
|
|
G(Expr1, Var, Début, FinN1)Þ0 G(Expr1, Var, Début, Fin) ÞLG(Expr1, Var, Fin+1, DébutN1) if Fin < DébutN1 Le formules d'addition utilisées sont extraites des références ci-dessous : Ronald L. Graham, Donald E. Knuth et Oren Patashnik. Concrete Mathematics: A Foundation for Computer Science. Reading, Massachusetts: Addison-Wesley, 1994. |
|
|
Catalogue > |
||||||||||
|
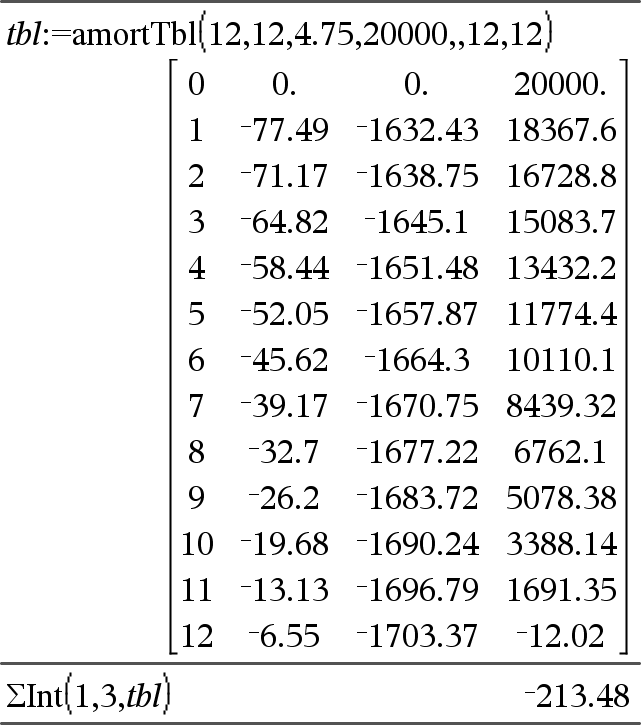
GInt(NPmt1, NPmt2, N, I, PV,[Pmt], [FV], [PpY], [CpY], [PmtAt], [valArrondi])Þvaleur GInt(NPmt1,NPmt2,tblAmortissement)Þvaleur Fonction d'amortissement permettant de calculer la somme des intérêts au cours d'une plage de versements spécifiée. NPmt1 et NPmt2 définissent le début et la fin de la plage de versements. N, I, PV, Pmt, FV, PpY, CpY et PmtAt sont décrits dans le tableau des arguments TVM, ici.
valArrondi spécifie le nombre de décimales pour arrondissement. Valeur par défaut=2. GInt(NPmt1,NPmt2,tblAmortissement) calcule la somme de l'intérêt sur la base du tableau d'amortissement tblAmortissement. L'argument tblAmortissement doit être une matrice au format décrit à tblAmortissement(), ici. Remarque : voir également GPrn() ci dessous et Bal(), ici. |
|
|
Catalogue > |
||||||||||
|
GPrn(NPmt1, NPmt2, N, I, PV, [Pmt], [FV], [PpY], [CpY], [PmtAt], [valArrondi])Þvaleur GPrn(NPmt1,NPmt2,tblAmortissement)Þvaleur Fonction d'amortissement permettant de calculer la somme du capital au cours d'une plage de versements spécifiée. NPmt1 et NPmt2 définissent le début et la fin de la plage de versements. N, I, PV, Pmt, FV, PpY, CpY et PmtAt sont décrits dans le tableau des arguments TVM, ici.
valArrondi spécifie le nombre de décimales pour arrondissement. Valeur par défaut=2. GPrn(NPmt1,NPmt2,tblAmortissement) calcule la somme du capital sur la base du tableau d'amortissement tblAmortissement. L'argument tblAmortissement doit être une matrice au format décrit à tblAmortissement(), ici. Remarque : voir également GInt() ci-dessus et Bal(), ici. |
|
|
Touches /k |
|
|
# ChaîneNomVar Fait référence à la variable ChaîneNomVar. Permet d'utiliser des chaînes de caractères pour créer des noms de variables dans une fonction. |
Crée ou fait référence à la variable xyz.
Donne la valeur de la variable (r) dont le nom est stocké dans la variable s1. |
|
Touche i |
|
|
mantisseEexposant Saisit un nombre en notation scientifique. Ce nombre est interprété sous la forme mantisse × 10exposant. Conseil : pour entrer une puissance de 10 sans passer par un résultat de valeur décimale, utilisez 10^entier. Remarque : vous pouvez insérer cet opérateur à partir du clavier de l'ordinateur en entrant @E. Par exemple, entrez 2.3@E4 pour avoir 2.3E4. |
|
|
Touche 1 |
|
|
Liste1g Þliste Matrice1g Þmatrice Cette fonction permet d'utiliser un angle en grades en mode Angle en degrés ou en radians. En mode Angle en radians, multiplie Expr1 par p/200. En mode Angle en degrés, multiplie Expr1 par g/100. En mode Angle en grades, donne Expr1 inchangée. Remarque : vous pouvez insérer ce symbole à partir du clavier de l'ordinateur en entrant @g. |
En mode Angle en degrés, grades ou radians :
|
|
Touche 1 |
|
|
Liste1RÞliste Matrice1RÞmatrice Cette fonction permet d'utiliser un angle en radians en mode Angle en degrés ou en grades. En mode Angle en degrés, multiplie l'argument par 180/p. En mode Angle en radians, donne l'argument inchangé. En mode Angle en grades, multiplie l'argument par 200/p. Conseil : utilisez Rsi vous voulez forcer l'utilisation des radians dans une définition de fonction quel que soit le mode dominant lors de l'utilisation de la fonction. Remarque : vous pouvez insérer ce symbole à partir du clavier de l'ordinateur en entrant @r. |
En mode Angle en degrés, grades ou radians :
|
|
Touche 1 |
|
|
Liste1¡Þliste Matrice1¡Þmatrice Cette fonction permet d'utiliser un angle en degrés en mode Angle en grades ou en radians. En mode Angle en radians, multiplie l'argument par p/180. En mode Angle en degrés, donne l'argument inchangé. En mode Angle en grades, multiplie l'argument par 10/9. Remarque : vous pouvez insérer ce symbole à partir du clavier de l'ordinateur en entrant @d. |
En mode Angle en degrés, grades ou radians :
En mode Angle en radians : |
|
Touches /k |
|||||||
|
dd¡mm'ss.ss''Þexpression ddNombre positif ou négatif mmNombre positif ou nul ss.ssNombre positif ou nul Donne dd+(mm/60)+(ss.ss/3600). Ce format d'entrée en base 60 permet :‑
Remarque : faites suivre ss.ss de deux apostrophes ('') et non de guillemets ("). |
En mode Angle en degrés :
|
|
Touches /k |
|
|
[Rayon,±q_Angle]Þvecteur (entrée polaire) [Rayon,±q_Angle,Valeur_Z]Þvecteur (entrée cylindrique) [Rayon,±q_Angle,±q_Angle]Þvecteur (entrée sphérique) Donne les coordonnées sous forme de vecteur, suivant le réglage du mode Format Vecteur : rectangulaire, cylindrique ou sphérique. Remarque : vous pouvez insérer ce symbole à partir du clavier de l'ordinateur en entrant @<. |
En mode Angle en radians et avec le Format vecteur réglé sur : rectangulaire
cylindrique
sphérique
|
|
(Grandeur ± Angle)ÞvaleurComplexe (entrée polaire) Saisit une valeur complexe en coordonnées polaires (r±q). L'Angle est interprété suivant le mode Angle sélectionné. |
En mode Angle en radians et en mode Format complexe Rectangulaire :
|
|
Voir “Éléments vides”, ici. |
|
|
|
|
|
Catalogue > |
|
|
10^ (Valeur1)Þvaleur 10^ (Liste1)Þliste Donne 10 élevé à la puissance de l'argument. Dans le cas d'une liste, donne 10 élevé à la puissance des éléments de Liste1. |
|
|
10^(matriceCarrée1)ÞmatriceCarrée Donne 10 élevé à la puissance de matriceCarrée1. Ce calcul est différent du calcul de 10 élevé à la puissance de chaque élément. Pour plus d'informations sur la méthode de calcul, reportez-vous à cos(). matriceCarrée1 doit être diagonalisable. Le résultat contient toujours des chiffres en virgule flottante. |
|
|
Catalogue > |
|
|
Valeur1 ^/Þvaleur Liste1 ^/Þliste Donne l'inverse de l'argument. Dans le cas d'une liste, donne la liste des inverses des éléments de Liste1. |
|
|
matriceCarrée1 ^/ÞmatriceCarrée Donne l'inverse de matriceCarrée1. matriceCarrée1 doit être une matrice carrée non singulière. |
|
|
touches /k |
||||||||||
|
Expr | ExprBooléen1 [ Expr | ExprBooléen1 [ Le symbole (« | ») est utilisé comme opérateur binaire. L'opérande à gauche du symbole | est une expression. L'opérande à droite du symbole | spécifie une ou plusieurs relations destinées à affecter la simplification de l'expression. Plusieurs relations après le symbole | peuvent être reliées au moyen d'opérateurs logiques « L'opérateur "sachant que" fournit trois types de fonctionnalités de base :
|
|
|||||||||
|
Les substitutions se présentent sous la forme d'une égalité, telle que x=3 ou y=sin(x). Pour de meilleurs résultats, la partie gauche doit être une variable simple. Expr | Variable = valeur substituera une valeur à chaque occurrence de Variable dans Expr. |
|
|||||||||
|
Les contraintes d'intervalle se présentent sous la forme d'une ou plusieurs inéquations reliées par des opérateurs logiques « |
|
|||||||||
|
Les exclusions utilisent l'opérateur « différent de » (/= ou ƒ) pour exclure une valeur spécifique du calcul. |
|
Touche /h |
|
|
Liste & Var Matrix & Var Expr & Fonction(Param1,...) Liste & Fonction(Param1,...) Matrice & Fonction(Param1,...) Si la variable Var n'existe pas, celle-ci est créée par cette instruction et est initialisée à Valeur, Liste ou Matrice. Si Var existe déjà et n'est pas verrouillée ou protégée, son contenu est remplacé par Valeur, Liste ou Matrice. Remarque : vous pouvez insérer cet opérateur à partir du clavier de l'ordinateur en entrant =: comme un raccourci. Par exemple, tapez pi/4 =: Mavar. |
|
|
Touches /t |
|
|
Var := Liste Var := Matrice Fonction(Param1,...) := Expr Fonction(Param1,...) := Liste Fonction(Param1,...) := Matrice Si la variable Var n'existe pas, celle-ci est créée par cette instruction et est initialisée à Valeur, Liste ou Matrice. Si Var existe déjà et n'est pas verrouillée ou protégée, son contenu est remplacé par Valeur, Liste ou Matrice. |
|
|
Touches /k |
|
|
© [texte] © traite texte comme une ligne de commentaire, vous permettant d'annoter les fonctions et les programmes que vous créez. © peut être utilisé au début ou n'importe où dans la ligne. Tous les caractères situés à droite de ©, jusqu'à la fin de la ligne, sont considérés comme partie intégrante du commentaire. Remarque pour la saisie des données de l’exemple : Pour obtenir des instructions sur la saisie des définitions de fonction ou de programme sur plusieurs lignes, consultez la section relative à la calculatrice dans votre guide de produit. |
|
|
Touches 0B, touches 0H |
|
|
0b nombreBinaire 0h nombreHexadécimal Indique un nombre binaire ou hexadécimal, respectivement. Pour entrer un nombre binaire ou hexadécimal, vous devez utiliser respectivement le préfixe 0b ou 0h, quel que soit le mode Base utilisé. Un nombre sans préfixe est considéré comme décimal (base 10). Le résultat est affiché en fonction du mode Base utilisé. |
En mode base Dec :
En mode base Bin :
En mode base Hex :
|









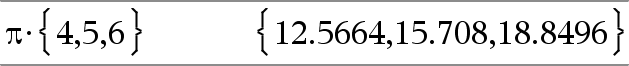






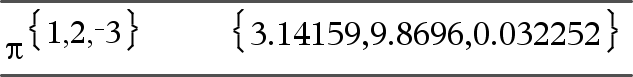


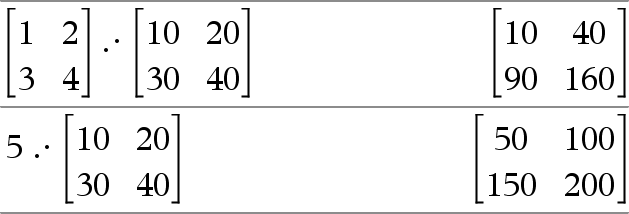
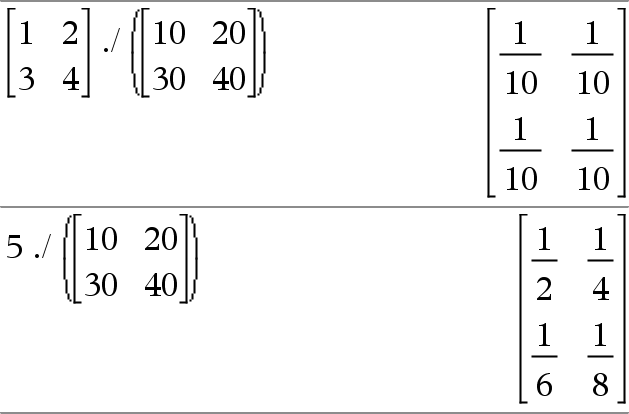
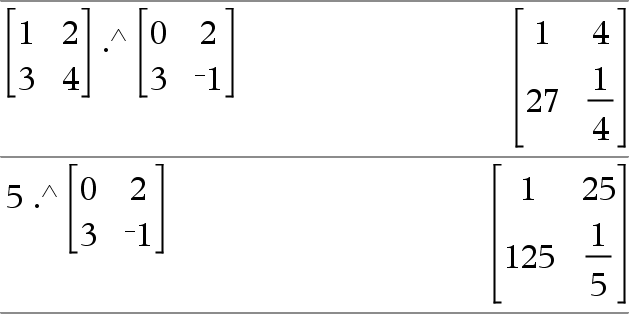
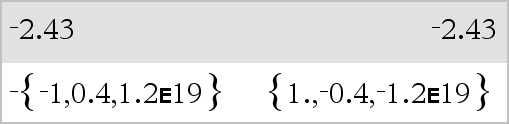
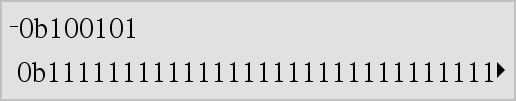
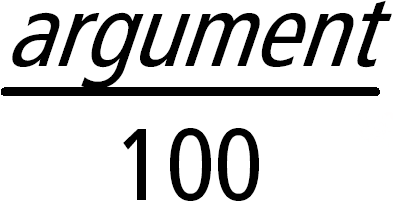
 .
.