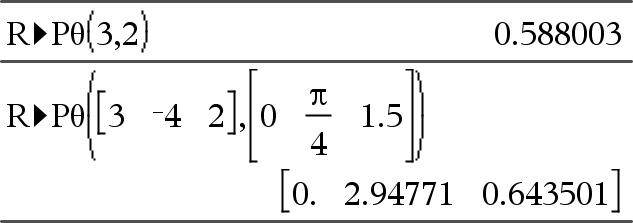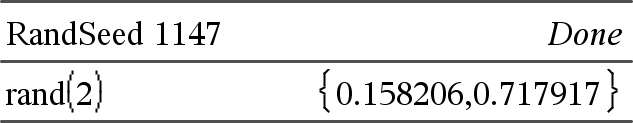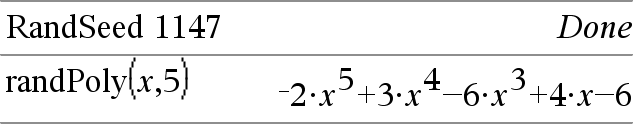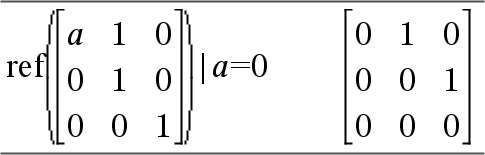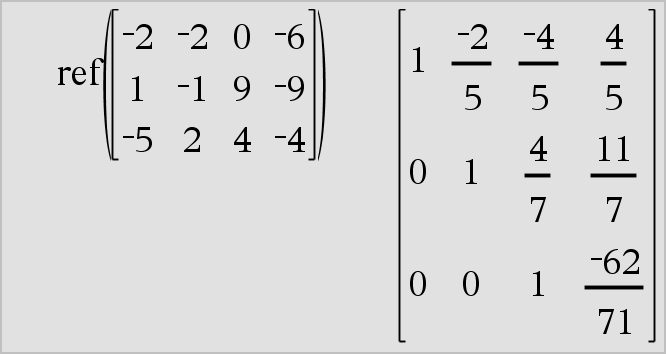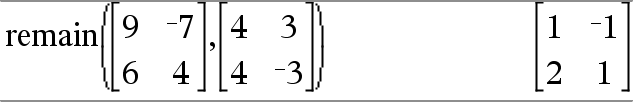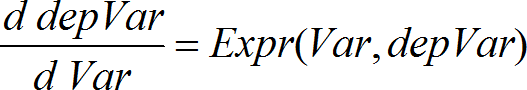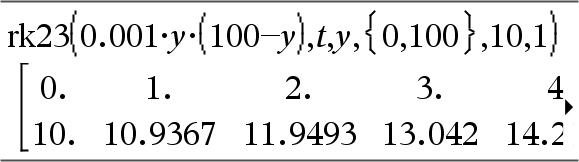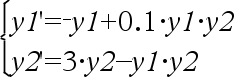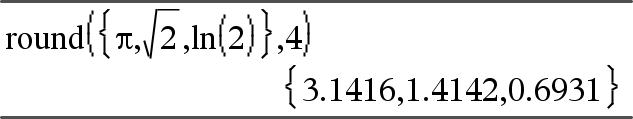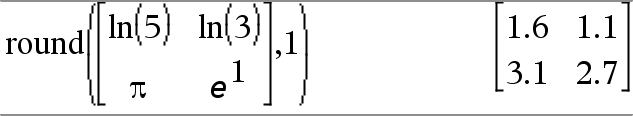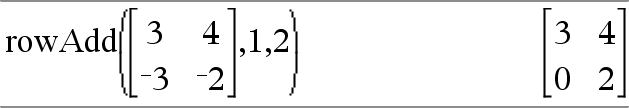|
Luettelo > |
|
|
Laskee yhtäpitävän θ-koordinaatin argumenttiparille Huomaa: Vastaus lasketaan aste-, graadi- tai radiaanikulmana käytössä olevan kulmatila-asetuksen mukaisesti. Huomaa: Voit syöttää tämän funktion tietokoneen näppäimistöltä kirjoittamalla R@>Ptheta(...). |
Astekulmatilassa:
|
|
Luettelo > |
|
|
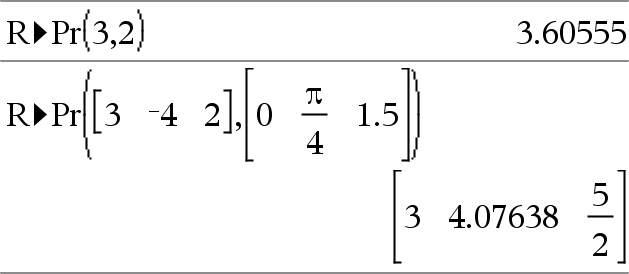
Laskee yhtäpitävän r-koordinaatin argumenttiparille (x,y). Huomaa: Voit syöttää tämän funktion tietokoneen näppäimistöltä kirjoittamalla R@>Pr(...). |
Radiaanikulmatilassa:
|
|
Luettelo > |
|
|
Muuntaa argumentin radiaanikulmayksikköön. Huomaa: Voit syöttää tämän operaattorin tietokoneen näppäimistöltä kirjoittamalla @>Rad. |
Astekulmatilassa:
|
|
Luettelo > |
|
|
rand() ⇒ lauseke rand() laskee satunnaisen arvon välillä 0 ja 1. rand(Kokeiden lkm) laskee listan, joka sisältää Kokeiden lkm satunnaista arvoa välillä 0 ja 1. |
Aseta satunnainen siemenluku.
|
|
Luettelo > |
|
|
randBin(n, p) ⇒ lauseke randBin(n, p) laskee satunnaisen reaaliluvun määrätystä binomijakaumasta. randBin(n, p, Kokeiden lkm) laskee listan, joka sisältää Kokeiden lkm satunnaista reaalilukua määrätystä binomijakaumasta. |
|
|
Luettelo > |
|
|
randInt(Muutt.alaraja,Muutt.yläraja) ⇒ lauseke randInt(Muutt.alaraja,Muutt.yläraja) laskee satunnaisen kokonaisluvun rajojenMuutt.alaraja jaMuutt.yläraja määräämällä kokonaislukuvälillä. randInt(Muutt.alaraja,Muutt.yläraja ,Kokeiden lkm) laskee listan, joka sisältääKokeiden lkm satunnaista kokonaislukua määrätyllä välillä. |
|
|
Luettelo > |
|
|
randMat(numRivit, numSarakkeet) ⇒ matriisi Laskee välillä -9 ja 9 määrätylle mitalle kokonaislukumatriisin. Kummankin argumentin on sievennyttyvä kokonaisluvuksi. |
Huomaa: Tämän matriisin arvot muuttuvat aina, kun painat ·. |
|
Luettelo > |
|
|
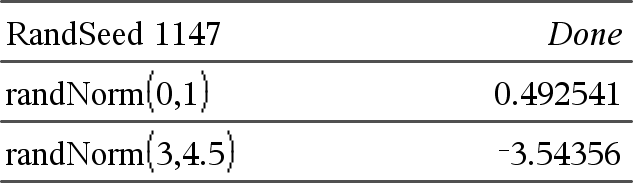
randNorm(μ, σ) ⇒ lauseke randNorm(μ, σ) laskee desimaaliluvun määrätystä normaalijakaumasta. Luku voi olla mikä tahansa reaaliluku, mutta se keskittyy voimakkaasti välille [μ−3•σ, μ+3•σ]. randNorm(μ, σ, Kokeiden lkm) listan (list), joka sisältää Kokeiden lkm desimaalilukua määrätystä normaalijakaumasta. |
|
|
Luettelo > |
|
|
randPoly(Muutt, Aste) ⇒ lauseke Laskee polynomin muuttujasta Muutt määrätyssä järjestyksessä Aste. Kertoimet ovat satunnaisia kokonaislukuja välillä −9 ja 9. Johtava kerroin ei ole 0. Asteen on oltava 0–99. |
|
|
Luettelo > |
|
|
randSample(List,Kokeiden lkm[,noRepl]) ⇒ lista Laskee satunnaisesta otoksesta listan, joka koostuu valinnoista Kokeiden lkm listasta List valinnaisena otoksen korvaaminen muulla (noRepl=0), tai ilman otoksen korvaamista (noRepl=1). Oletusarvona on otoksen korvaaminen |
|
|
Luettelo > |
|
|
RandSeed Luku Jos Luku = 0, tämä asettaa siemenluvut satunnaislukugeneraattorin tehdasasetuksiin. Jos Luku ≠ 0, sitä käytetään luomaan kaksi siemenlukua, jotka tallennetaan järjestelmän muuttujiin siemen1 ja siemen2 |
|
|
Luettelo > |
|
|
real(Arvo1) ⇒ arvo Laskee argumentin reaalilukuosan. |
|
|
real(List1) ⇒ lista Laskee kaikkien alkutekijöiden reaaliosat |
|
|
real(Matriisi1) ⇒ matriisi Laskee kaikkien alkutekijöiden reaaliosat. |
|
|
Luettelo > |
|
|
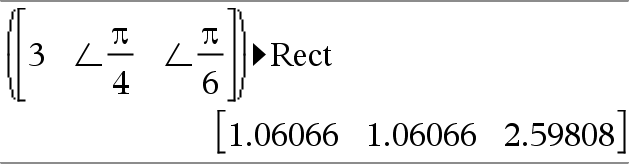
Vectr ►Rect Huomaa: Voit syöttää tämän operaattorin tietokoneen näppäimistöltä kirjoittamalla @>Rect. Näyttää Vektorin suorakulmamuodossa [x, y, z] Vektorin on oltava kooltaan 2 tai 3, ja se voi olla rivi tai sarake. Huomaa: ►Rect on näyttömuodon ohje, ei muunnosfunktio. Voit käyttää komentoa ainoastaan syöterivin lopussa, eikä se päivitä arvoa ans. Huomaa: Katso myös ►Polar, täältä. |
|
|
kompleksiArvo ►Rect Näyttää kompleksisen arvon complexValuesuorakulmaisessa muodossa a+bi. Arvolla complexValue voi olla mikä tahansa kompleksinen muoto. Syöte reiθaiheuttaa kuitenkin virheen astekulmatilassa. Huomaa: Polaarisessa syötteessä (r∠θ) on käytettävä sulkeita. |
Radiaanikulmatilassa:
Huomaa: Näppäilläksesi merkin ∠ valitse se Luettelon symboliluettelosta. |
|
Luettelo > |
|||||||
|
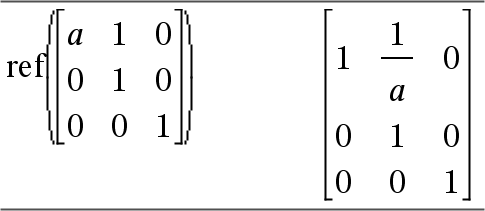
ref(Matriisi1[, Tol]) ⇒ matriisi Laskee matriisin Matriisi1 rivi-echelon-muodossa. Valinnaisesti kaikkia matriisin elementtejä käsitellään nollana, jos niiden itseisarvo on pienempi kuin Tol. Tätä toleranssia käytetään vain, jos matriisissa on liukulukusyötteitä eikä se sisällä symbolisia muuttujia, joille ei ole määrätty arvoa. Muussa tapauksessa komentoa Tol ei huomioida.
Vältä määrittelemättömiä alkutekijöitä matriisissa Matriisi1. Tuloksena saattaa olla odottamattomia vastauksia. Jos esimerkiksi a on määrittelemätön seuraavassa lausekkeessa, näkyviin tulee varoitusviesti, ja vastaus näyttää seuraavalta:
Varoitus näkyy, koska yleistetty alkutekijä 1/a ei olisi mahdollinen lausekkeelle a=0. Voit välttää tämän tallentamalla etukäteen arvon a:lle tai käyttämällä rajoittavaa (“|”)-operaattoria arvon korvaamiseksi, kuten on esitetty seuraavassa esimerkissä.
Huomaa: Katso myös rref(), here. |
|
|
Luettelo > |
|||||||||||
|
RefreshProbeVars Pääset mittausarvoon kaikista TI-Basic-ohjelmaan kytketyistä antureista.
|
Esimerkki
Huomaa: Tätä voi käyttää myös TI-Innovator™i-laitteen keskiössä. |
|
Luettelo > |
|
|
Laskee ensimmäisen argumentin jäännöksen toisen argumentin suhteen seuraavien identtisten yhtälöiden määritelmien mukaisesti: remain(x,0) x |
|
|
Tämän seurauksena huomaa, ettäremain(−x,y) − remain(x,y). Vastaus on joko nolla tai samanmerkkinen kuin ensimmäinen argumentti. Huomaa: Katso myös mod(), täältä. |
|
|
Luettelo > |
|||||||||||||||||||
|
Ohjelmointikomento: Keskeyttää ohjelman ja näyttää valintaruudun, jossa on viesti kehotemerkkijono sekä syöttöruutu käyttäjän antamaa vastausta varten. Kun käyttäjä kirjoittaa vastauksen ja klikkaa OK-painiketta, syöttöruudun sisältö määrätään muuttujalle var. Jos käyttäjä klikkaa Cancel, ohjelma etenee hyväksymättä mitään syötteitä. Ohjelma käyttää muuttujan muutt aikaisempaa arvoa, jos var on jo määritelty. Valinnainen NäytäLippu -argumentti voi olla mikä tahansa lauseke.
|
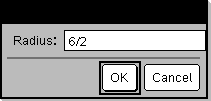
Määrittele ohjelma: Määrittele pyydä_demo()=Ohjelma
Aja ohjelma ja kirjoita vastaus: Pyydä_demo()
Vastaus OK-näppäimen painamisen jälkeen: Säde: 6/2 |
||||||||||||||||||
|
Valinnainen statusVar argumentti laskee ohjelmalle tavan määritellä, kuinka käyttäjä on sulkenut valintaikkunan. Huomaa, että statusVar vaatii NäytäLippu -argumentin.
func()-argumentin avulla ohjelma voi tallentaa käyttäjän vastauksen funktion määritelmäksi. Tämä syntaksi toimii ikään kuin käyttäjä suorittaisi komennon: Määrittele func(arg1, ...argn) = käyttäjän vastaus Sen jälkeen ohjelma voi käyttää määriteltyä funktiota func(). Komennon promptStringpitäisi opastaa käyttäjää syöttämään sopiva käyttäjän vastaus, joka täydentää funktion määritelmän. Huomaa: Voit käyttää Pysäytä ohjelma, joka sisältää komennon Request loputtoman silmukan sisällä:
Huomaa: Katso myös |
Määrittele ohjelma: Määrittele polynomi()=Ohjelma
Aja ohjelma ja kirjoita vastaus: polynomi()
Tulos, kun x^3+3x+1 on syötetty ja valittu OK: Reaalilukujuuret ovat: {-0.322185} |
|
Luettelo > |
|||||||||||||
|
Ohjelmointikomento: Toimii samalla tavalla kuin Request-komennon ensimmäinen syntaksi paitsi, että käyttäjän vastaus tulkitaan aina merkkijonoksi. VastakohtaisestiRequest-komento tulkitsee vastauksen lausekkeeksi, jollei käyttäjä merkitse sitä lainausmerkkien (““) sisään. Huomaa: Voit käyttääRequestStr -komentoa käyttäjän määrittelemässä ohjelmassa, mutta ei funktiossa. Pysäytä ohjelma, joka sisältää
Huomaa: Katso myös |
Määrittele ohjelma: Määrittele requestStr_demo()=Ohjelma
Aja ohjelma ja kirjoita vastaus: requestStr_demo()
Vastaus OK-näppäimen painamisen jälkeen (Huomaa, että jos NäytäLippu-argumentti on 0, kehote ja vastaus eivät näy historiassa):
requestStr_demo() Vastauksessa on 5 merkkiä. |
|
Luettelo > |
|
|
Return [Laus] Laskee lausekkeen Lausfunktion tuloksena Käytetään lohkon Func...EndFunc sisällä. Huomaa: Käytä Return ilman argumenttia lohkossa Prgm...EndPrgm poistuaksesi ohjelmasta. Huomaa esimerkkiä syöttäessäsi: Ohjeet monirivisten ohjelmien ja funktion määritysten syöttämisestä löytyvät tuotteen ohjekirjan Laskin-osiosta. |
|
|
Luettelo > |
|
|
oikea(List1[, Num]) ⇒ lista Laskee oikeanpuoleisimmat Num-alkutekijät, jotka sisältyvät listaan List1. Jos jätät pois komennon Num, laskee kaiken listasta List1. |
|
|
right(lädemerkkijono[, Num]) ⇒ merkkijono Laskee oikeanpuoleisimmat Num-merkit, jotka sisältyvät merkkijonoon lähdemerkkijono Jos jätät pois komennonNum, laskee kaiken lähdemerkkijonosta. |
|
|
right(Vertailu) ⇒ lauseke Laskee yhtälön tai epäyhtälön oikean puolen. |
|
Luettelo > |
|
|
Käyttää Runge-Kutta-menetelmää järjestelmän ratkaisuun Expr on oikea puoli, joka määrittelee tavallisen differentiaaliyhtälön (ODE). SystemOfExpr on oikeiden puolten ryhmä, joka määrittelee ODE-yhtälöiden järjestelmän (vastaa riippuvaisten muuttujien järjestystä kohdassa ListOfDepVars). ListOfExpr on oikeiden puolten luettelo, joka määrittelee ODE-yhtälöiden järjestelmän (vastaa riippuvaisten muuttujien järjestystä kohdassa ListOfDepVars). Var on riippumaton muuttuja. ListOfDepVars on riippuvaisten muuttujien luettelo. {Var0, VarMax} on kahden elementin lista, joka määrää funktion integroimaan muuttujasta Var0 to VarMax. ListOfDepVars0 on lista riippuvaisten muuttujien alkuarvoja. Jos VarStep on arvoltaan nollasta eroava numero: merkki(VarStep) = merkki(VarMax-Var0) ja ratkaisut lasketaan muuttujalla Var0+i*VarStep kaikille i=0,1,2,… niin, että Var0+i*VarStep on alueella [muutt0,VarMax] (muuttujalla VarMax ei ehkä ole ratkaisuarvoa). jos VarStep sievenee nollaksi, ratkaisut lasketaan "Runge-Kutta" -muuttujan Muutt arvoilla. diftol on virhetoleranssi (oletuksena 0.001). |
Differentiaaliyhtälö: y'=0.001*y*(100-y) ja y(0)=10 Jos haluat nähdä koko vastauksen, paina 5 ja siirrä sen jälkeen osoitinta painikkeilla 7 ja 8. Sama yhtälö, jossa diftol on asetettu 1.E−6 Yhtälöryhmä:
kun y1(0)=2 and y2(0)=5
|
|
Luettelo > |
|
|
root(Arvo) ⇒ juuri
juuri(Arvo1, Arvo2) laskee arvona Arvo2 arvonArvo1 juuren. Arvo1 voi olla reaalinen tai kompleksinen liukulukuvakio, kokonaisluku tai kompleksinen rationaalilukuvakio Huomaa: Katso myös N:s juuri -malli, täältä. |
|
|
Luettelo > |
|
|
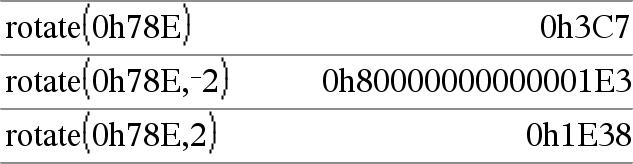
rotate(Kokonaisluku1[,KiertojenLkm]) ⇒ kokonaisluku Kiertää bittejä binaarisessa kokonaisluvussa. Voit syöttää luvun Kokonaisluku1 minä tahansa kantalukuna; se muunnetaan automaattisesti 64 bitin binaarimuotoon. Jos Kokonaisluku1 on liian suuri tälle muodolle, symmetrinen modulo-operaatio sovittaa sen alueelle sopivaksi Katso lisätietoa kohdasta ►Kantaluku2, täältä. |
Binaarisessa kantalukutilassa:
Jos haluat nähdä koko vastauksen, paina 5 ja siirrä sen jälkeen osoitinta painikkeilla 7 ja 8. |
|
Jos KiertojenLkm on positiivinen, kierto on vasemmalle. Jos KiertojenLkm on negatiivinen, kierto on oikealle. Oletusarvo on −1 (kierrä oikealle yksi bitti). Esimerkki, kierrossa oikealle: |
Heksadesimaalisessa kantalukutilassa:
|
|
Jokainen bitti kiertyy oikealle. 0b00000000000001111010110000110101 Oikeanpuoleisin bitti siirtyy vasemmaisimmaksi. tuottaa: 0b10000000000000111101011000011010 Vastaus näkyy kantalukutilan mukaisesti. |
Tärkeää: Binaariluvun edelle tulee aina merkitä etumerkki 0b ja heksadesimaaliluvun edelle 0h (nolla, ei O-kirjain). |
|
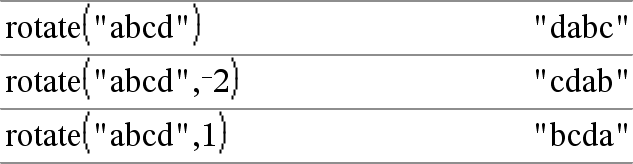
rotate(Lista1[,KiertojenLkm]) ⇒ lista Laskee Lista1:nkopion, jota on kierretty oikealle tai vasemmalle KiertojenLkm:n elementtien määrittämän määrän. Ei muuta Listaa1. Jos KiertojenLkm on positiivinen, kierto on vasemmalle. Jos KiertojenLkm on negatiivinen, kierto on oikealle. Oletusarvo on −1 (kierrä oikealle yksi elementti). |
Desimaalisessa kantalukutilassa:
|
|
rotate(Merkkijono1[,KiertojenLkm]) ⇒ merkkijono LaskeeMerkkijono1:n kopion, jonka on kiertänyt oikealle tai vasemmalle KiertojenLkm:n merkkien määrittämän määrän. Ei muuta Merkkijono1:tä Jos KiertojenLkm on positiivinen, kierto on vasemmalle. Jos KiertojenLkm on negatiivinen, kierto on oikealle. Oletusarvo on −1 (kierrä oikealle yksi merkki). |
|
|
Luettelo > |
|
|
round(Arvo1[, numeroa]) ⇒ lauseke Laskee argumentin pyöristettynä jättäen desimaalipisteen jälkeen määrätyn määrän numeroita. numeroiden on oltava kokonaisluku välillä 0–12. Jos numeroita ei sisällytetä, laskee argumentin pyöristettynä 12 merkitykselliseen numeroon. Huomaa: Näytettävät numerot -tila saattaa vaikuttaa näyttöön. |
|
|
round(Lista1[, numerot]) ⇒ lista Pyöristää alkutekijöiden listan jättäen desimaalipisteen jälkeen määrätyn määrän numeroita. |
|
|
round(Matriisi1[, numerot]) ⇒ matriisi Pyöristää alkutekijöiden matriisin jättäen desimaalipisteen jälkeen määrätyn määrän numeroita. |
|
|
Luettelo > |
|
|
rowAdd(Matriisi1, rIndeksi1, rIndeksi2) ⇒ matriisi Laskee matriisin Matriisi1 kopion rivirIndeksi2 korvattuna rivien summallarIndeksi1 ja rIndeksi2. |
|
|
Luettelo > |
|
|
rowDim(Matriisi) ⇒ lauseke Laskee Matriisin sisältämien rivien lukumäärän. Huomaa: Katso myös colDim(), täältä. |
|
|
Luettelo > |
|
|
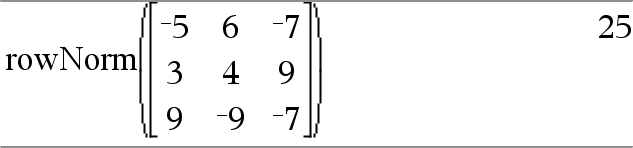
rowNorm(Matriisi) ⇒ lauseke Laskee Matriisin riveillä olevien elementtien itseisarvojen summien maksimin. Huomaa: Kaikkien matriisien alkutekijöiden on sievennyttävä luvuiksi. Katso myös colNorm(), täältä. |
|
|
Luettelo > |
|
|
rowSwap(Matriisi1, rIndeksi1, rIndeksi2) ⇒ matriisi Laskee matriisin Matriisi1, jossa rivien rIndeksi1 ja rIndeksi2 paikkoja on vaihdettu. |
|
|
Luettelo > |
|||||||
|
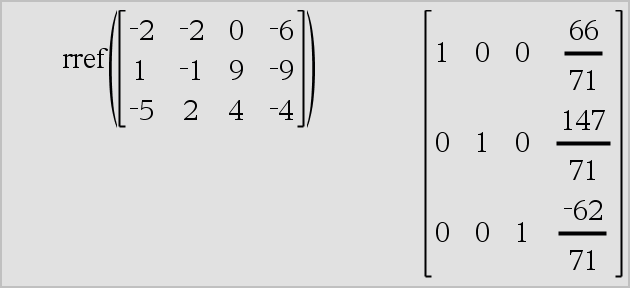
rref(Matriisi1[, Tol]) ⇒ matriisi Laskee matriisin Matriisi1 pelkistetyn rivi-echelon-muodon. |
|
||||||
|
Valinnaisesti kaikkia matriisin elementtejä käsitellään nollana, jos niiden itseisarvo on pienempi kuin Tol. Tätä toleranssia käytetään vain, jos matriisissa on liukulukusyötteitä eikä se sisällä symbolisia muuttujia, joille ei ole määritelty arvoa. Muussa tapauksessa komentoa Tol ei huomioida.
Huomaa: Katso myös ref(), here. |