B

 

bal()

Katalogi >

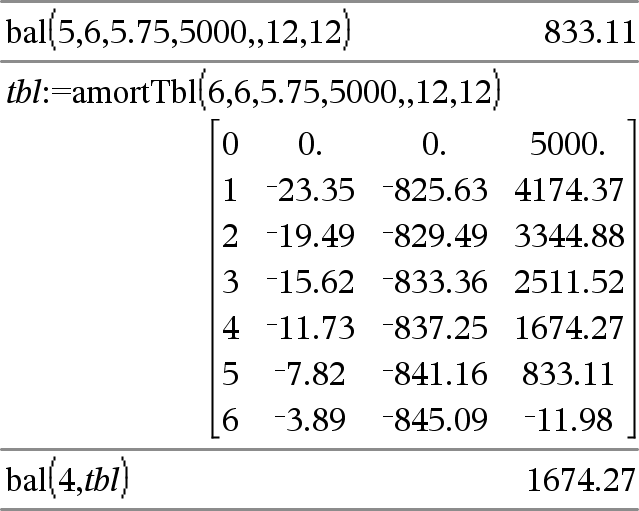
bal(NPmt,N,I,PV ,[Pmt], [FV], [PpY], [CpY], [PmtAt], [pyörArvo])Þarvo

bal(NPmt,amortTable)Þarvo

Lyhennysfunktio, joka laskee määritetyn maksuerän jälkeen jäljellä olevan velkasaldon.

N, I, PV, Pmt, FV, PpY, CpY ja PmtAt on kuvattu TVM-argumenttien taulukossa, täältä.

NPmt määrittää sen maksuerän numeron, jonka jälkeen velkasaldo halutaan laskea.

N, I, PV, Pmt, FV, PpY, CpY ja PmtAt on kuvattu TVM-argumenttien taulukossa, täältä.

• Jos jätät argumentin Pmt pois, sen oletusarvoksi tulee Pmt=tvmPmt(N,I,PV,FV,PpY,CpY,PmtAt).
• Jos jätät argumentin FV pois, sen oletusarvoksi tulee FV=0.
• Argumenttien PpY, CpY ja PmtAt oletusarvot ovat samat kuin TVM-funktioilla.

pyörArvo määrittää pyöristyksessä käytettävien desimaalien määrän. Oletusarvo=2.

bal(NPmt,amortTable) laskee maksueränumeron NPmt jälkeen jäljellä olevan velkasaldon lyhennystaulukon amortTable perusteella. amortTable-argumentin on oltava matriisi, joka on kohdassa amortTbl() kuvatun muotoinen, katso täältä.

Huomaa: Katso myös GInt() ja GPrn(), täältä.

 

►Base2 (4Kantaluku2)

Katalogi >

Kokonaisluku1 ►Base2Þkokonaisluku

Huomaa: Voit syöttää tämän operaattorin tietokoneen näppäimistöltä kirjoittamalla @>Base2.

Muuttaa Kokonaisluku1:n binaariluvuksi. Binaariluvuissa on aina etuliite 0b ja heksadesimaaliluvuissa etuliite 0h.

Ilman etuliitettä Kokonaisluku1:ä käsitellään desimaalilukuna (kantaluku 10). Vastaus näkyy binaarilukuna kantalukutilasta riippumatta.

Negatiiviset luvut näytetään kahden komplementteina. Esimerkki:

N1 näkyy muodossa
0hFFFFFFFFFFFFFFFF  heksadesimaalisessa kantalukutilassa
0b111...111 (64  ykköstä)  binaarisessa kantalukutilassa

N263 näkyy muodossa
0h8000000000000000  heksadesimaalisessa kantalukutilassa
0b100...000 (63 zeros)  binaarisessa kantalukutilassa

Jos syötät desimaalikokonaisluvun, joka on etumerkillisen, 64 bitin binaarimuodon lukualueen ulkopuolella, laskin käyttää symmetristä modulo-operaatiota, jotta arvo saadaan oikealle alueelle. Tarkastele seuraavassa esitettyjä esimerkkejä lukualueen ulkopuolella olevista arvoista.

263 muuttuu muotoon N263 ja näkyy muodossa
0h8000000000000000  heksadesimaalisessa kantalukutilassa
0b100...000 (63 zeros)  binaarisessa kantalukutilassa

264 muuttuu muotoon 0 ja näkyy
0h0  heksadesimaalisessa kantalukutilassa
0b0  binaarisessa kantalukutilassa

N263 N 1 muuttuu muotoon 263 N 1 ja näkyy muodossa
0h7FFFFFFFFFFFFFFF  heksadesimaalisessa kantalukutilassa
0b111...111 (64  ykköstä)  binaarisessa kantalukutilassa

 

 

4Base10 (►Kantaluku10)

Katalogi >

Kokonaisluku1 ►Base10Þkokonaisluku

Huomaa: Voit syöttää tämän operaattorin tietokoneen näppäimistöltä kirjoittamalla @>Base10.

Muuttaa Kokonaisluku1:n desimaaliluvuksi (kantaluku 10). Binaarisen syötteen edellä tulee aina olla etumerkki 0b ja heksadesimaalisen syötteen edellä 0h.

0b binaariluku
0h heksadesimaaliluku

Nolla, ei O-kirjain, jonka perässä on b tai h.

Binaariluvussa voi olla enintään 64 numeroa. Heksadesimaaliluvussa voi olla enintään 16 numeroa.

Ilman etuliitettä Kokonaisluku1:ä käsitellään desimaalilukuna. Vastaus näkyy desimaalilukuna kantalukutilasta riippumatta.

 

►Base16 (4Kantaluku16)

Katalogi >

Kokonaisluku1 ►Base16Þkokonaisluku

Huomaa: Voit syöttää tämän operaattorin tietokoneen näppäimistöltä kirjoittamalla @>Base16.

Muuttaa Kokonaisluku1:n heksadesimaaliluvuksi. Binaariluvuissa on aina etuliite 0b ja heksadesimaaliluvuissa etuliite 0h.

0b binaariluku
0h heksadesimaaliluku

Nolla, ei O-kirjain, jonka perässä on b tai h.

Binaariluvussa voi olla enintään 64 numeroa. Heksadesimaaliluvussa voi olla enintään 16 numeroa.

Ilman etuliitettä Kokonaisluku1:ä käsitellään desimaalilukuna (kantaluku 10). Vastaus näkyy heksadesimaalilukuna kantalukutilasta riippumatta.

Jos syötät desimaalikokonaisluvun, joka on liian suuri etumerkilliselle, 64 bitin binaarimuodolle, laskin käyttää symmetristä modulo-operaatiota, jotta arvo saadaan oikealle alueelle.

Jos syötät desimaalikokonaisluvun, joka on etumerkillisen, 64 bitin binaarimuodon lukualueen ulkopuolella, laskin käyttää symmetristä modulo-operaatiota, jotta arvo saadaan oikealle alueelle. Lisätietoja, katso 4Base2, täältä.

 

binomCdf()

Katalogi >

binomCdf(n,p)Þlista

binomCdf(n,p,alaraja,yläraja)Þluku, jos alaraja ja yläraja ovat lukuja, lista, jos alaraja ja yläraja ovat listoja

binomCdf(n,p,yläraja)kun P(0{X{yläraja)Þluku, jos yläraja on luku, lista, jos yläraja on lista

Laskee kumulatiivisen todennäköisyyden diskreetille binomiselle jakaumalle, jossa toistojen määrä on n ja jokaisen toiston onnistumistodennäköisyys on p.

Kun P(X { yläraja), aseta alaraja=0

 

 

binomPdf()

Katalogi >

binomPdf(n,p)Þlista

binomPdf(n,p,XVal)Þluku, jos XVal on luku, lista, jos XVal on lista

Laskee todennäköisyyden diskreetille binomiselle jakaumalle, jossa toistojen määrä on n ja jokaisen toiston onnistumistodennäköisyys on p.