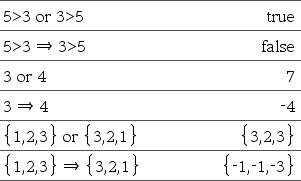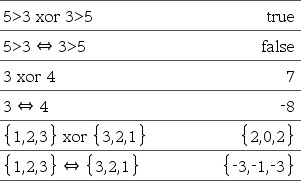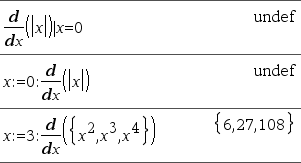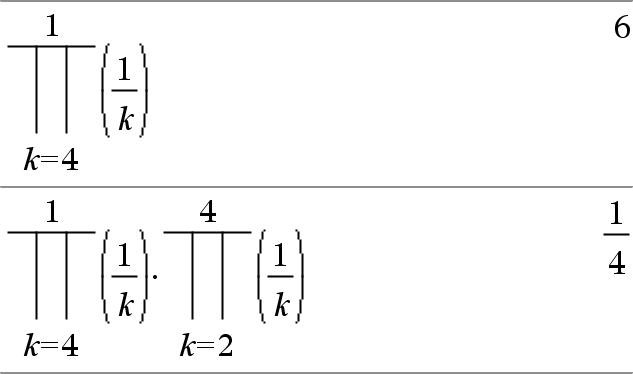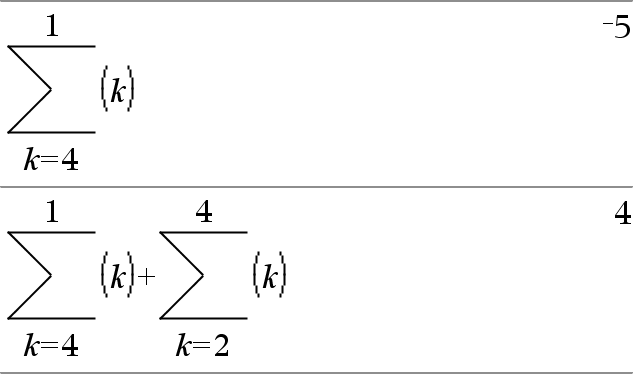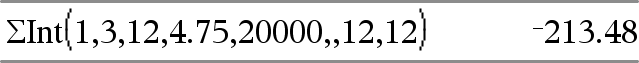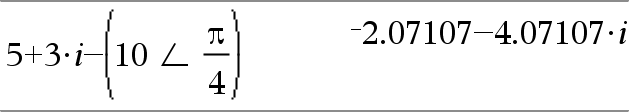|
+ painike |
|
|
Laskee kahden argumentin summan. |
|
|
Lista1 + Lista2ÞlistaMatriisi1 Määrittää listan (tai matriisin), joka sisältää Lista1:n ja Lista2:n (tai Matriisi1:n ja Matriisi2:n) vastaavien elementtien summat. Argumenttien tulee olla mitoiltaan samanlaisia. |
|
|
|
|
|
Laskee matriisin, jossa Arvo on lisätty jokaiseen elementtiin Matriisi1:n diagonaalimatriisissa. Matriisi1 :n on oltava neliö. Huomaa: Käytä merkintää .+ (piste plus), kun haluat lisätä lausekkeen jokaiseen elementtiin. |
|
|
- painike |
|
|
|
|
|
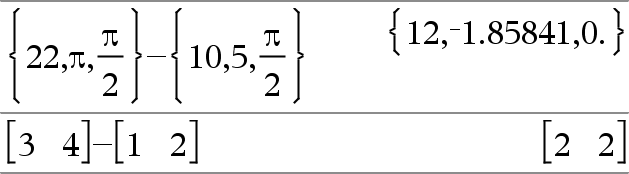
Lista1 N Lista2Þlista Matriisi1 N Matriisi2Þmatriisi Vähentää Lista2:n (tai Matriisi2:n) jokaisen elementin Lista1:n (tai Matriisi1:n) vastaavasta elementistä ja antaa tuloksena vastaukset. Argumenttien tulee olla mitoiltaan samanlaisia. |
|
|
|
|
|
Arvo N Matriisi1 laskee Arvon matriisin kerrottuna identtisellä matriisilla miinus Matriisi1. Matriisi1:n on oltava neliö. Matriisi1 N Arvo laskee Arvo n matriisin kerrottuna identtisellä matriisilla, joka on vähennetty Matriisi1:stä. Matriisi1:n on oltava neliö. Huomaa: Käytä merkintää .N (piste miinus), kun haluat vähentää lausekkeen jokaisesta elementistä. |
|
|
r painike |
|
|
Laskee kahden argumentin tulon. |
|
|
Lista1·Lista2Þlista Luo listan, joka sisältää Lista1:n ja Lista2:n vastaavien elementtien tulot. Listojen tulee olla mitoiltaan samanlaisia. |
|
|
Matriisi1 ·Matriisi2Þmatriisi Laskee Matriisi1:n ja Matriisi2:n matriisitulon. Matriisi1:n sarakkeiden lukumäärän on oltava sama kuin Matriisi2:n rivien lukumäärä. |
|
|
|
|
|
Määrittää matriisin, joka sisältää Arvon ja kunkin Matriisi1:n elementin tulon. Huomaa: Käytä merkintää .·(piste kerro), kun haluat kertoa lausekkeen jokaisella elementillä. |
|
|
p painike |
|
|
Laskee osamäärän Arvo1 jaettuna Arvo2:lla. Huomaa: Katso myös Murtolukumalli, täältä. |
|
|
Lista1 à Lista2Þlista Määrittää listan, joka sisältää osamäärät laskutoimituksista Lista1 jaettuna Lista2:lla. Listojen tulee olla mitoiltaan samanlaisia. |
|
|
Arvo à Lista1 Þ lista Lista1 à Arvo Þ lista
|
|
|
Matriisi1 à Arvo Þ matriisi Laskee matriisin, joka sisältää osamäärät laskutoimituksesta Matriisi1àArvo. Huomaa: Käytä merkintää . / (piste jaa), kun haluat jakaa lausekkeen jokaisella elementillä. |
|
|
l painike |
|
|
Arvo1 ^ Arvo2 Þ arvo Lista1 ^ Lista2 Þ lista Laskee ensimmäisen argumentin korotettuna toisen argumentin potenssiin. Huomaa: Katso myös Eksponenttimalli, täältä. Jos kyseessä on lista, laskee Lista1:n elementit korotettuna Lista2:n vastaavien elementtien potenssiin. Reaalilukujen alueella murtolukupotenssit, joilla on supistetut eksponentit ja parittomat nimittäjät, käyttävät reaalista aluetta versus pääalue kompleksitilassa. |
|
|
|
|
|
|
|
|
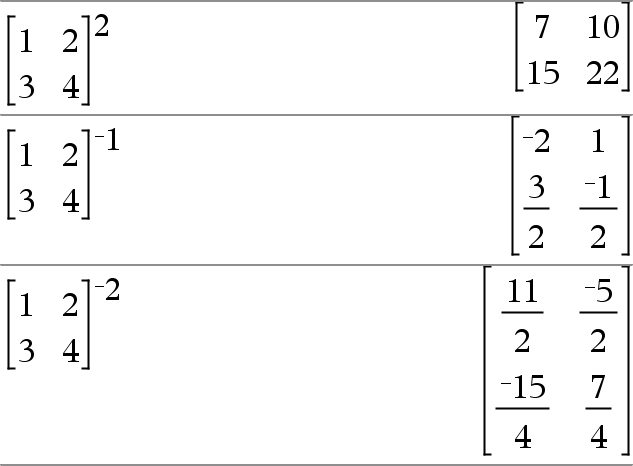
neliömatriisi1 ^ kokonaisluku Þ matriisi Laskee neliömatriisi1:n korotettuna kokonaisluvun kokonaisluku potenssiin. neliömatriisi1:n on oltava neliömatriisi. Jos kokonaisluku = L1, laskee käänteismatriisin. |
|
|
q painike |
|
|
Arvo12 Þ arvo Laskee argumentin neliön. Lista12 Þ lista Laskee listan, joka sisältää Lista1:n elementtien neliöt. neliömatriisi12 Þ matriisi Laskee neliömatriisi1:n matriisineliön. Tämä ei ole sama kuin kunkin elementin neliön laskeminen. Käytä merkintää .^2, kun haluat laskea jokaisen elementin neliön. |
|
|
^+ painikkeet |
|
|
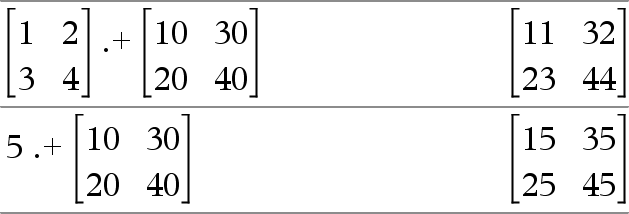
Matriisi1 .+ Matriisi2 Þ matriisi
Matriisi1 .+ Matriisi2 laskee matriisin, joka on Matriisi1:n ja Matriisi2:n vastaavien elementtiparien summa. Arvo .+ Matriisi1 laskee matriisin, joka on Arvon ja kunkin Matriisi1:n elementin summa. |
|
|
^- painikkeet |
|
|
Matriisi1 .N Matriisi2 Þ matriisi Matriisi1 .NMatriisi2 laskee matriisin, joka on Matriisi1:n ja Matriisi2:n vastaavien elementtiparien välinen erotus.
|
|
|
^r painikkeet |
|
|
Matriisi1 .· Matriisi2 Þ matriisi
Matriisi1 .· Matriisi2 laskee matriisin, joka on Matriisi1:n ja Matriisi2:n vastaavien elementtiparien tulo.
|
|
|
^p painikkeet |
|
|
Matriisi1 . / Matriisi2 Þ matriisi Arvo . / Matriisi1 Þ matriisi Matriisi1 ./ Matriisi2 laskee matriisin, joka on Matriisi1:n ja Matriisi2:n vastaavien elementtiparien osamäärä.
|
|
|
^l painikkeet |
|
|
Matriisi1.^ Matriisi2 Þ matriisi
Matriisi1 .^ Matriisi2 laskee matriisin, jossa Matriisi2:n jokainen elementti on eksponentti Matriisi1:n vastaavalle elementille.
|
|
|
v painike |
|
|
LLista1 Þ lista LMatriisi1 Þ matriisi Laskee argumentin negaation. Kun kyseessä on lista tai matriisi, määrittää kaikkien elementtien negaatiot. Jos argumentti on binaarinen tai heksadesimaalinen kokonaisluku, negaatio antaa kakkosen komplementin. |
Jos haluat nähdä koko vastauksen, paina 5 ja siirrä sen jälkeen osoitinta painikkeilla 7 ja 8. |
|
/k painikkeet |
|
|
Arvo1 % Þ arvo Lista1 % Þ lista Matriisi1 % Þ matriisi Määrittää Kun kyseessä on lista tai matriisi, määrittää listan tai matriisin, jossa jokainen elementti on jaettu luvulla 100. |
Huom: Vastauksen pakottaminen likimääräiseksi: Kämmenlaite: Paina / ·.
|
|
= painike |
|
|
Laus1 = Laus2ÞBoolen lauseke Lista1 = Lista2Þ Boolen lista Matriisi1 = Matriisi2Þ Boolen matriisi Antaa totuusarvon tosi, jos Laus1 määritetään olevan yhtä kuin Laus2. Antaa totuusarvon epätosi, jos Laus1 määritetään olevan ei yhtä kuin Laus2. Kaikissa muissa tapauksissa vastauksena on yhtälön sievennetty muoto. Listojen ja matriisien kohdalla vastauksena on vertailuja elementti elementiltä. Huomaa esimerkkiä syöttäessäsi: Ohjeet monirivisten ohjelmien ja funktion määritysten syöttämisestä löytyvät tuotteen ohjekirjan Laskin-osiosta. |
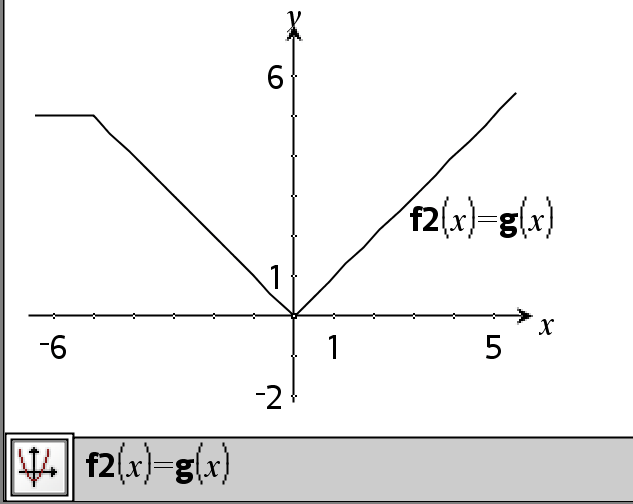
Esimerkkifunktio, jossa on käytetty matematiikkatestisymboleita: =, ƒ, <, {, >, |
Funktion g(x) kuvaajan piirtämisen tulos
|
|
/= painikkeet |
|
|
Laus1 ƒ Laus2 Þ Boolen lauseke Lista1ƒ Lista2 Þ Boolen lista Matriisi1ƒ Matriisi2 Þ Boolen matriisi Antaa totuusarvon tosi, jos Laus1 määritetään olevan ei yhtä kuin Laus2. Antaa totuusarvon epätosi, jos Laus1 määritetään olevan yhtä kuin Laus2. Kaikissa muissa tapauksissa vastauksena on yhtälön sievennetty muoto. Listojen ja matriisien kohdalla vastauksena on vertailuja elementti elementiltä. Huomaa: Voit syöttää tämän operaattorin näppäimistöltä kirjoittamalla /= |
Katso esimerkki kohdasta “=” (on yhtä kuin). |
|
/= painikkeet |
|
|
Laus1 < Laus2 Þ Boolen lauseke Lista1 < Lista2 Þ Boolen lista Matriisi1 < Matriisi2 Þ Boolen matriisi Antaa totuusarvon tosi, jos Laus1 määritetään olevan pienempi kuin Laus2. Antaa totuusarvon epätosi, jos Laus1 määritetään olevan suurempi tai yhtä suuri kuin Laus2. Kaikissa muissa tapauksissa vastauksena on yhtälön sievennetty muoto. Listojen ja matriisien kohdalla vastauksena on vertailuja elementti elementiltä. |
Katso esimerkki kohdasta “=” (on yhtä kuin). |
|
/= painikkeet |
|
|
Laus1 { Laus2 Þ Boolen lauseke Lista1{ Lista2 Þ Boolen lista Matriisi1{ Matriisi2 Þ Boolen matriisi Antaa totuusarvon tosi, jos Laus1 määritetään olevan pienempi tai yhtä suuri kuin Laus2. Antaa totuusarvon epätosi, jos Laus1 määritetään olevan suurempi kuin Laus2. Kaikissa muissa tapauksissa vastauksena on yhtälön sievennetty muoto. Listojen ja matriisien kohdalla vastauksena on vertailuja elementti elementiltä. Huomaa: Voit syöttää tämän operaattorin näppäimistöltä kirjoittamalla <= |
Katso esimerkki kohdasta “=” (on yhtä kuin). |
|
/= painikkeet |
|
|
Laus1 > Laus2 Þ Boolen lauseke Lista1 > Lista2 Þ Boolen lista Matriisi1 > Matriisi2 Þ Boolen matriisi Antaa totuusarvon tosi, jos Laus1 määritetään olevan suurempi kuin Laus2. Antaa totuusarvon epätosi, jos Laus1 määritetään olevan pienempi tai yhtä suuri kuin Laus2. Kaikissa muissa tapauksissa vastauksena on yhtälön sievennetty muoto. Listojen ja matriisien kohdalla vastauksena on vertailuja elementti elementiltä. |
Katso esimerkki kohdasta “=” (on yhtä kuin). |
|
/= painikkeet |
|
|
Laus1 | Laus2 Þ Boolen lausek Lista1 | Lista2 Þ Boolen lista Matriisi1 | Matriisi2 Þ Boolen matriisi Antaa totuusarvon tosi, jos Laus1 määritetään olevan suurempi tai yhtä suuri kuin Laus2. Antaa totuusarvon epätosi, jos Laus1 määritetään olevan pienempi kuin Laus2. Kaikissa muissa tapauksissa vastauksena on yhtälön sievennetty muoto. Listojen ja matriisien kohdalla vastauksena on vertailuja elementti elementiltä. Huomaa: Voit syöttää tämän operaattorin näppäimistöltä kirjoittamalla >= |
Katso esimerkki kohdasta “=” (on yhtä kuin). |
|
/= näppäimet |
|
|
BoolenLaus1 ÞBoolenLaus2antaa vastauksena Boolen lausekkeen BoolenList1Þ BoolenList2 antaa vastauksena Boolen listan BoolenMatriisi1Þ BoolenMatriisi2 antaa vastauksena Boolen matriisin Kokonaisluku1Þ Kokonaisluku2 antaa vastauksena kokonaisluvun Arvioi lausekkeen Listojen ja matriisien kohdalla vastauksena on vertailuja elementti elementiltä. Huomaa: Voit syöttää tämän operaattorin näppäimistöltä kirjoittamalla => |
|
|
/= näppäimet |
|
|
BoolenLaus1 ÛBoolenLaus2antaa vastauksena Boolen lausekkeen BoolenList1Û BoolenList2 antaa vastauksena Boolen listan BoolenMatriisi1Û BoolenMatriisi2 antaa vastauksena Boolen matriisin Kokonaisluku1Û Kokonaisluku2 antaa vastauksena kokonaisluvun Antaa vastauksena Listojen ja matriisien kohdalla vastauksena on vertailuja elementti elementiltä. Huomaa: Voit syöttää tämän operaattorin näppäimistöltä kirjoittamalla <=> |
|
|
º painike |
|
|
Arvo1! Þ arvo Lista1! Þ lista Matriisi1! Þ matriisi Määrittää argumentin kertoman. Jos kyseessä on lista tai matriisi, määrittää listan tai matriisin elementtien kertomista. |
|
|
/k painikkeet |
|
|
Merkkijono1 & Merkkijono2 Þ merkkijono Antaa vastauksena tekstimerkkijonon, joka on Merkkijono2 liitettynä Merkkijono1:een. |
|
|
Katalogi > |
|
|
d(Laus1, Muutt[, Aste])Þarvo d(Lista1, Muutt[, Aste])Þlista d(Matriisi1, Muutt[, Aste])Þmatriisi Lukuun ottamatta tilannetta, jolloin käytät ensimmäistä syntaksia, muuttujaan Muutt on tallennettava numeerinen arvo ennen funktion d() sieventämistä. Katso esimerkkejä.
Asteen, mikäli se otetaan mukaan, on oltava 1 tai 2. Oletusarvo on 1. Huomaa: Voit syöttää tämän funktion näppäimistöltä kirjoittamalla
|
|
|
Tarkastele oikealla olevaa esimerkkiä. Yhtälön x·(x^2+x)^(1/3), kun x=0, ensimmäinen derivaatta on yhtä kuin 0. Koska alalausekkeen (x^2+x)^(1/3) ensimmäinen derivaatta kuitenkin on määrittämätön pisteessä x=0, ja tällä arvolla lasketaan koko lausekkeen derivaatta, d() ilmaisee vastauksen määrittämättömänä ja näyttää varoitusviestin.
|
|
|
Katalogi > |
|
|
‰(Laus1, Muutt, Ala, Ylä) Þ arvo Laskee Laus1:n integraalin muuttujan Muutt suhteen välillä Ala - Ylä olevista arvoista. Funktiota voi käyttää myös laskettaessa numeerisesti määrätty integraali käyttäen samaa menetelmää kuin nInt(). Huomaa: Voit syöttää tämän funktion näppäimistöltä kirjoittamalla integral(...). Huomaa: Katso myös nInt(), täältä, ja Määrätyn integraalin malli, täältä. |
|
|
/q painikkeet |
|
|
‡ (Lista1)Þlista Laskee argumentin neliöjuuren. Kun kyseessä on lista, laskee kaikkien Lista1:n elementtien neliöjuuret. Huomaa: Voit syöttää tämän funktion näppäimistöltä kirjoittamalla sqrt(...) Huomaa: Katso myös Neliöjuurimalli, täältä. |
|
|
Katalogi > |
|
|
P(Laus1, Muutt, Matala, Korkea)Þlauseke Huomaa: Voit syöttää tämän funktion näppäimistöltä kirjoittamalla prodSeq(...). Sieventää Laus1:n jokaisen Muutt:n arvon suhteen väliltä Matala - Korkea ja laskee vastausten tulon. Huomaa: Katso myös Kertolaskumalli (P), täältä. |
|
|
P(Laus1, Muutt, Matala, MatalaN1)Þ1 P(Laus1, Muutt, Matala, Korkea) Esimerkkien kertolaskukaavat on otettu seuraavasta viitteestä: Ronald L. Graham, Donald E. Knuth, and Oren Patashnik. Concrete Mathematics: A Foundation for Computer Science. Reading, Massachusetts: Addison-Wesley, 1994. |
|
|
Katalogi > |
|
|
G(Laus1, Muutt, Matala, Korkea)Þlauseke Huomaa: Voit syöttää tämän funktion näppäimistöltä kirjoittamalla sumSeq(...). Sieventää Laus1:n jokaisen muuttujan Muutt arvon suhteen väliltä Matala - Korkea ja laskee vastausten summan. Huomaa: Katso myös Summamalli, täältä. |
|
|
G(Laus1, Muutt, Matala, MatalaN1)Þ0 |
|
|
G(Laus1, Muutt, Matala, Korkea) Esimerkkien yhteenlaskukaavat on otettu seuraavasta viitteestä: Ronald L. Graham, Donald E. Knuth, and Oren Patashnik. Concrete Mathematics: A Foundation for Computer Science. Reading, Massachusetts: Addison-Wesley, 1994. |
|
|
Katalogi > |
||||||||||
|
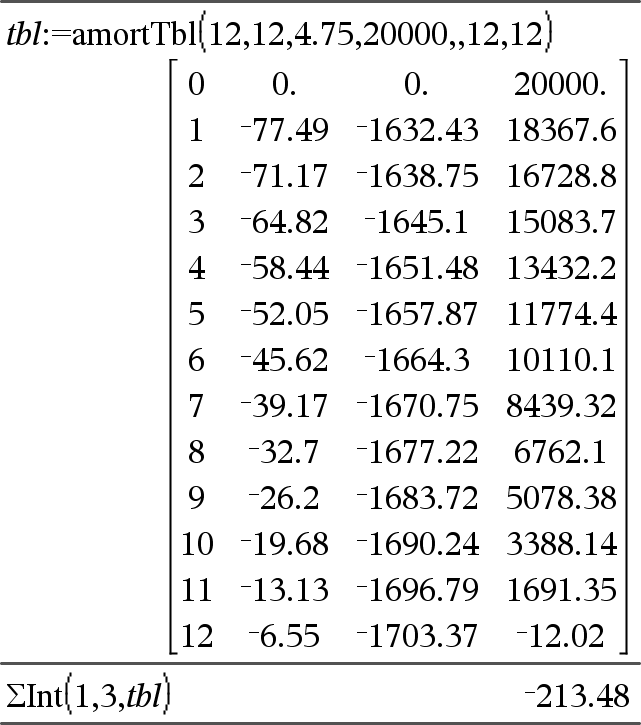
GInt(NPmt1, NPmt2, N, I, PV ,[Pmt], [FV], [PpY], [CpY], [PmtAt], [pyörArvo])Þarvo GInt(NPmt1,NPmt2,amortTable)Þarvo Lyhennystoiminto, joka laskee koron summan määritetyn maksueräjakson ajalta. NPmt1 ja NPmt2 määrittävät maksujakson alku- ja loppurajat. N, I, PV, Pmt, FV, PpY, CpY ja PmtAt on kuvattu TVM-argumenttien taulukossa, täältä.
pyörArvo määrittää pyöristyksessä käytettävien desimaalien määrän. Oletusarvo=2. GInt(NPmt1,NPmt2,amortTable) laskee koron summan lyhennystaulukon amortTable mukaisesti. amortTable-argumentin on oltava matriisi, joka on kohdassa amortTbl() kuvatun muotoinen, katso täältä. Huomaa: Katso myös GPrn(), jäljempänä, sekä Bal(), täältä. |
|
|
Katalogi > |
||||||||||
|
GPrn(NPmt1, NPmt2, N, I, PV, [Pmt], [FV], [PpY], [CpY], [PmtAt], [pyörArvo])Þarvo GPrn(NPmt1,NPmt2,amortTable)Þarvo Lyhennystoiminto, joka laskee pääoman summan määritetyn maksujakson ajalta. NPmt1 ja NPmt2 määrittävät maksujakson alku- ja loppurajat. N, I, PV, Pmt, FV, PpY, CpY ja PmtAt on kuvattu TVM-argumenttien taulukossa, täältä.
pyörArvo määrittää pyöristyksessä käytettävien desimaalien määrän. Oletusarvo=2. GPrn(NPmt1,NPmt2,amortTable) laskee pääoman summan lyhennystaulukon amortTable perusteella. amortTable-argumentin on oltava matriisi, joka on kohdassa amortTbl() kuvatun muotoinen, katso täältä. Huomaa: Katso myös GInt(), edellä, sekä Bal(), täältä. |
|
|
/k painikkeet |
|
|
# muuttNimiMerkkijono Viittaa muuttujaan, jonka nimi on muuttNimiMerkkijono. Tällä operaattorilla voit luoda muuttujanimiä funktion sisältä merkkijonojen avulla. |
Luo muuttujan xyz tai viittaa siihen.
Laskee arvon muuttujalle (r), jonka nimi on tallennettu muuttujaan s1. |
|
i painike |
|
|
mantissaEeksponentti Syöttää luvun kymmenpotenssimuodossa. Luku tulkitaan seuraavasti: mantissa × 10eksponentti. Vinkki: Jos haluat syöttää 10-potenssin ilman, että vastauksena on desimaaliluku, käytä komentoa 10^kokonaisluku. Huomaa: Voit syöttää tämän operaattorin tietokoneen näppäimistöltä kirjoittamalla @E. Kirjoita esimerkiksi 2.3@E4, kun haluat syöttää 2.3E4. |
|
|
1 painike |
|
|
Laus1gÞlauseke Lista1gÞlista Matriisi1gÞmatriisi Tämän funktion avulla voit määrittää graadikulman ollessasi aste- tai radiaanikulmatilassa. Kun laskin on radiaanikulmatilassa, kertoo Laus1:n arvolla p/200. Kun laskin on astekulmatilassa, kertoo Laus1:n arvolla g/100. Graadikulmatilassa antaa vastauksena lausekkeen Laus1 muuttumattomana. Huomaa: Voit syöttää tämän symbolin tietokoneen näppäimistöltä kirjoittamalla @g. |
Aste-, graadi- tai radiaanikulmatilassa.
|
|
1 painike |
|
|
Lista1RÞlista Matriisi1RÞmatriisi Tämän funktion avulla voit määrittää radiaanikulman ollessasi aste- tai graadikulmatilassa. Kun laskin on astekulmatilassa, kertoo argumentin arvolla 180/p. Radiaanikulmatilassa antaa vastauksena argumentin muuttumattomana. Kun laskin on graadikulmatilassa, kertoo argumentin arvolla 200/p. Vinkki: Käytä komentoa R, jos haluat pakottaa funktion määritelmän yksiköksi radiaanit riippumatta tilasta, joka on käytössä funktion käytön aikana. Huomaa: Voit syöttää tämän symbolin tietokoneen näppäimistöltä kirjoittamalla @r. |
Aste-, graadi- tai radiaanikulmatilassa:
|
|
1 painike |
|
|
Lista1¡Þlista Matriisi1¡Þmatriisi Tämän funktion avulla voit määrittää astekulman ollessasi graadi- tai radiaanikulmatilassa. Kun laskin on radiaanikulmatilassa, kertoo argumentin arvolla p/180. Astekulmatilassa antaa vastauksena argumentin muuttumattomana. Kun laskin on graadikulmatilassa, kertoo argumentin arvolla 10/9. Huomaa: Voit syöttää tämän symbolin tietokoneen näppäimistöltä kirjoittamalla @d. |
Aste-, graadi- tai radiaanikulmatilassa:
Radiaanikulmatilassa: Huom: Vastauksen pakottaminen likimääräiseksi: Kämmenlaite: Paina / ·. |
|
/k painikkeet |
|||||||
|
dd¡mm'ss.ss''Þlauseke ddPositiivinen tai negatiivinen luku Laskee dd+(mm/60)+(ss.ss/3600). Tässä kantaluku‑60:n syötemuodossa voit:
Huomaa: Merkitse sekuntien ss.ss perään kaksi heittomerkkiä (''), ei lainausmerkkiä ("). |
Astekulmatilassa:
|
|
/k painikkeet |
|
|
[Säde,±q_Kulma]Þvektori [Säde,±q_Kulma,Z_Koordinaatti]Þvektori [Säde,±q_Kulma,±q_Kulma]Þvektori Laskee koordinaatit vektorina riippuen vektorimuototilan asetuksesta: suorakulma, sylinteri tai pallo. Huomaa: Voit syöttää tämän symbolin tietokoneen näppäimistöltä kirjoittamalla @<. |
Radiaanikulmatilassa ja kun vektorimuoto on asetettu valintaan:
|
|
(Magnitudi ± Kulma)ÞkompleksiArvo Syöttää kompleksilukuarvon (r±q) polaarisessa muodossa. Kulma tulkitaan nykyisen kulmatila-asetuksen mukaisesti. |
Radiaanikulmatilassa ja suorakulmakompleksimuodossa:
|
|
_ (alaviiva edustaa tyhjää elementtiä) |
KatsoTyhjät elementit, täältä. |
|
|
|
|
Katalogi > |
|
|
10^ (Arvo1)Þarvo 10^ (Lista1)Þlista Laskee luvun 10 korotettuna argumentin potenssiin. Jos kyseessä on lista, laskee luvun 10 korotettuna Lista1:n elementtien potenssiin. |
|
|
10^(neliömatriisi1)Þneliömatriisi Laskee luvun 10 korotettuna neliömatriisi1:n potenssiin. Tämä ei ole sama kuin kunkin elementin 10-potenssiin korottamisen laskeminen. Laskentamenetelmä on kuvattu kohdassa cos(). neliömatriisi1:n on oltava diagonalisoitavissa. Vastaus sisältää aina liukulukuja. |
|
|
Katalogi > |
|
|
Lista1 ^/Þlista Laskee argumentin käänteisluvun. Jos kyseessä on lista, laskee Lista1:n elementtien käänteisluvut. |
|
|
neliömatriisi1 ^/Þneliömatriisi Laskee neliömatriisi1:n käänteisluvun. neliömatriisi1:n oltava ei-singulaarinen neliömatriisi. |
|
|
/k -näppäimet |
||||||||||
|
Laus | Boolenlaus1 [ Laus | Boolenlaus1 [ Rajoittava (“|”)-symboli toimii binaarisena operaattorina. Operaattorin | vasemmalla puolella oleva operandi on lauseke. Operaattorin | oikealla puolella oleva operandi määrittää yhden tai useampia suhteita, joiden tarkoitus on vaikuttaa lausekkeen sieventämiseen. Operaattorin | jäljessä olevat useat suhteet on yhdistettävä loogisilla operaattoreilla “ Rajoittava operaattori tarjoaa kolme perustoimintoa:
|
|
|||||||||
|
Sijoitukset ovat yhtälön muodossa, kuten x=3 tai y=sin(x). Tehokkainta on, kun vasen puoli on yksinkertainen muuttuja. Laus | Muuttuja = arvo korvaa arvon jokaisessa Muuttujan esiintymiskohdassa lausekkeessa Laus. |
|
|||||||||
|
Välien rajoitusten muoto on yksi tai useampia epäyhtälöitä, jotka on yhdistetty loogisilla operaattoreilla “ |
|
|||||||||
|
Pois sulkemisessa käytetään suhdeoperaattoria “ei ole yhtä kuin” (/= tai ƒ), jonka avulla jokin tietty arvo suljetaan pois. |
|
/h painike |
|
|
Jos muuttujaa Muutt ei ole, laskin luo sen ja alustaa sen muotoon Arvo, Lista tai Matriisi. Jos muuttuja Muutt on jo olemassa eikä se ole lukittu tai suojattu, laskin korvaa sen sisällön arvolla Arvo, listalla Lista tai matriisilla Matriisi. Huomaa: Voit syöttää tämän operaattorin näppäimistöltä kirjoittamalla =: pikavalintana. Kirjoita esimerkiksi pi/4 =: myvar. |
|
|
/t painikkeet |
|
|
Muutt := Arvo Muutt := Lista Muutt := Matriisi Funktio(Param1,...) := Laus Funktio(Param1,...) := Lista Funktio(Param1,...) := Matriisi Jos muuttujaa Muutt ei ole, laskin luo muuttujan Muutt ja alustaa sen muotoon Arvo, Lista tai Matriisi. Jos muuttuja Muutt on jo olemassa eikä se ole lukittu tai suojattu, laskin korvaa sen sisällön Arvolla, Listalla tai Matriisilla. |
|
|
/k painikkeet |
|
|
© [teksti] © käsittelee tekstin kommenttirivinä, minkä avulla voit lisätä merkintöjä luomiisi funktioihin ja ohjelmiin. © voi olla rivin alussa tai missä tahansa rivin kohdassa. Kaikki merkin © jäljessä oleva, aina rivin loppuun saakka, on kommenttia. Huomaa esimerkkiä syöttäessäsi: Ohjeet monirivisten ohjelmien ja funktion määritysten syöttämisestä löytyvät tuotteen ohjekirjan Laskin-osiosta. |
|
|
0B painikkeet, 0H painikkeet |
|
|
0b binaariluku Määrittää binaari- (Ob) tai heksadesimaaliluvun (Oh). Syöttääksesi binaari- tai heksadesimaaliluvun sinun on syötettävä etuliite 0b tai 0h riippumatta kantalukutilasta. Ilman etuliitettä lukua käsitellään desimaalilukuna (kantaluku 10). Tulokset näytetään kantalukutilan mukaisesti. |
Desimaalisessa kantalukutilassa:
|









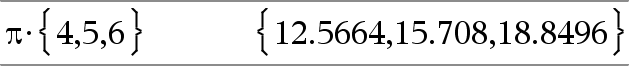






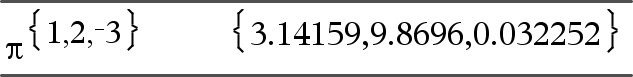




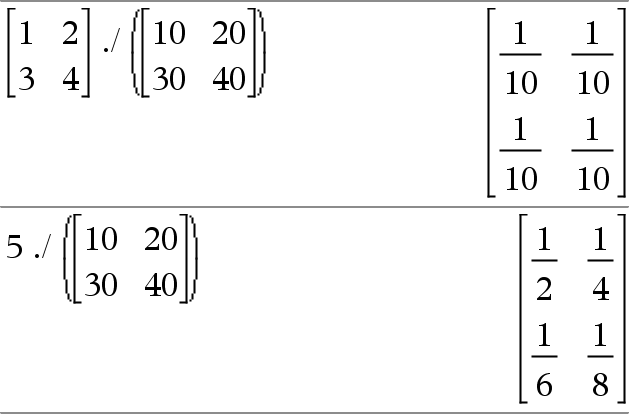
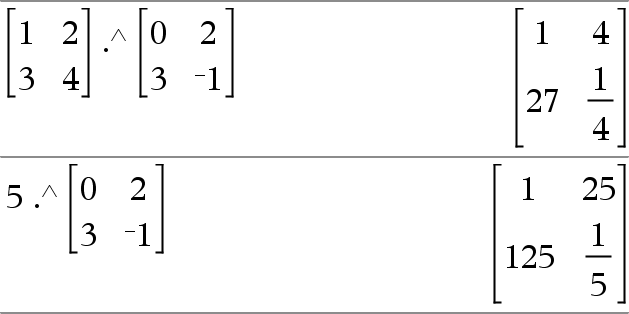
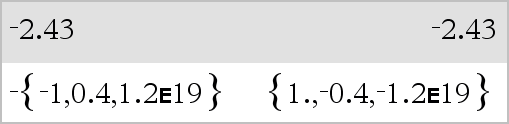
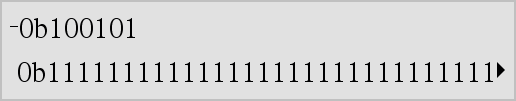
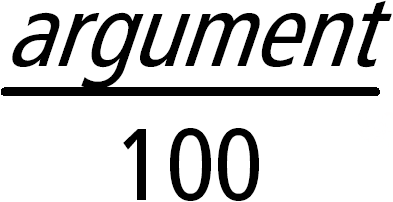
 .
.