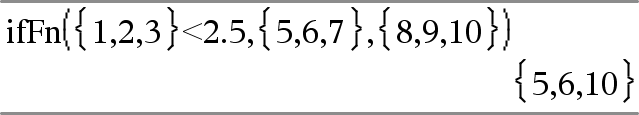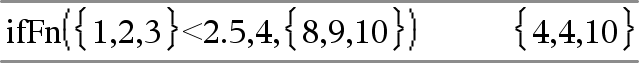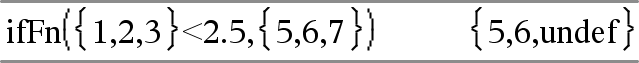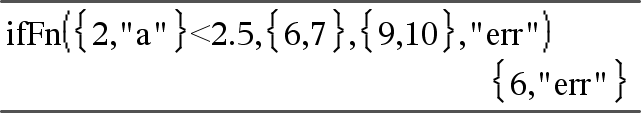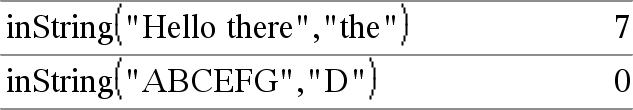|
Luettelo > |
|
|
identity(kokonaisluku) ⇒ matriisi Laskee identiteettimatriisin, jonka koko on kokonaisluku. Kokonaisluvun on oltava positiivinen kokonaisluku. |
|
|
Luettelo > |
|
|
JosBoolenLaus Jos BoolenLaus Niin Jos BoolenLaus on tosi, suorittaa yhden lausekkeen Lauseke tai lausekkeiden lohkon Lohko ennen suorituksen jatkamista. Jos BoolenLaus on epätosi, jatkaa suoritusta suorittamatta lauseketta tai lausekkeiden lohkoa. Lohko voi olla joko yksi lauseke tai sarja lausekkeita, jotka on erotettu toisistaan kaksoispisteellä (:) merkki. Huomaa esimerkkiä syöttäessäsi: Ohjeet monirivisten ohjelmien ja funktion määritysten syöttämisestä löytyvät tuotteen ohjekirjan Laskin-osiosta. |
|
|
Jos BoolenLaus, niin Jos BoolenLauson tosi, suorittaa Lohko1:n ja sen jälkeen jättää väliin Lohko2:n. Jos BoolenLaus on epätosi, ohittaa Lohko1:n, mutta suorittaa Lohko2:n. Lohko1 ja Lohko2 voivat olla yksi lauseke. |
|
|
Jos BoolenLaus1, niin Sallii haarautumisen Jos BoolenLaus1 on tosi, suorittaa Lohko1:n Jos BoolenLaus1 on epätosi, laskee BoolenLaus2:n jne. |
|
|
Luettelo > |
||||||||||||||||
|
ifFn(BoolenLaus,Arvo_Jos_tosi [,Arvo_Jos_epätosi [,Arvo_Jos_tuntematon]]) ⇒ lauseke, lista tai matriisi Laskee BoolenLaus (jokaiselle BoolenLaus ) elementille) ja antaa tuloksen noudattaen seuraavia sääntöjä:
Huomaa: Jos sievennetty BoolenLaus ilmaisu sisältää listan tai matriisin, kaikkien muiden lista- tai matriisiargumenttien on oltava samansuuruisia, ja myös tuloksen on oltava samansuuruinen. |
1:n testiarvo on alle 2.5, joten sen vastaava Arvo_Jos_tosi -elementti arvolle 5 kopioidaan vastausten listaan.
2:n testiarvo on alle 2.5, joten sitä vastaava Arvo_Jos_tosi-elementti arvolle 6 kopioidaan vastausten listaan.
Arvo_Jos_tosi on yksittäinen arvo ja vastaa mitä tahansa valittua sijaintia.
Arvoa Arvo_Jos_epätosi ei ole määritelty. Käytetään merkintää EiMäär
Yksi elementti valittu lausekkeesta Arvo_Jos_tosi. Yksi elementti valittu lausekkeesta Arvo_Jos_epätosi. |
|
Luettelo > |
|
|
imag(Arvo1) ⇒ arvo Laskee argumentin imaginaarisen osan. |
|
|
imag(Lista1) ⇒ lista Laskee listan alkutekijöiden imaginaarisista osista. |
|
|
imag(Matriisi1) ⇒ matriisi Laskee matriisin alkutekijöiden imaginaarisista osista. |
|
|
Epäsuora operaattori |
Katso #(), täältä. |
|
|
|
|
Luettelo > |
|
|
inString(srcMerkkijono, alaMerkkijono[, Alku]) ⇒ kokonaisluku Laskee merkin paikan merkkijonossa srcMerkkijono, jossa merkkijonon alaMerkkijono ensimmäinen esiintyminen alkaa. Alku, jos se sisältyy, määrää merkin paikan siinä merkkijonossa srcMerkkijono, josta haku alkaa. Oletusarvo = 1 (srcMerkkijonon ensimmäinen merkki). Jos srcMerkkijono ei sisällä alaMerkkijonoa tai Alku on srcMerkkijonon pituus, vastaus on nolla. |
|
|
Luettelo > |
|
|
Laskee suurimman kokonaisluvun, joka on pienempi tai yhtä suuri kuin argumentti. Tämä funktio on identtinen funktion pohjan floor() kanssa. Argumentti voi olla reaali- tai kompleksiluku. Kun kyseessä on lista tai matriisi, laskee kunkin elementin suurimman kokonaisluvun. |
|
|
Luettelo > |
|
|
intDiv(Luku1, Luku2) ⇒ kokonaisluku Laskee lausekkeen Luku1 ÷ Luku2) etumerkillisen kokonaislukuosan. Laskee sarjoille ja matriiseille lausekkeen (argumentti 1 ÷ argumentti 2) etumerkillisen kokonaislukuosan kullekin elementtiparille. |
|
|
Luettelo > |
|
|
Tällä toiminnolla suoritetaan seuraavaa: Kun ilmoitetaan xList, yList=f(xList) ja yPrimeList=f'(xList) jollekin tuntemattomalle funktiolle f, käytetään kuutiointerpolanttia funktion f määrittelemiseksi arvolla xArvo. Oletetaan, että xList on monotonisesti kasvavien tai laskevien numeroiden lista, mutta tämän toiminnon tuloksena saattaa olla arvo, vaikka se ei olisikaan sitä. Tämä toiminto käy läpi listan xList etsien väliä [xList[i], xList[i+1]], joka sisältää arvon xValue. Jos se löytää tällaisen välin, se palauttaa interpoloidun arvon funktiolle f(xValue); muuten se antaa tuloksen. Sarjojen xList, yList jayPrimeList on oltava samansuuruiset ≥ 2 ja sisällettävä lausekkeita, jotka sieventyvät luvuiksi.
|
Differentiaaliyhtälö:
Jos haluat nähdä koko vastauksen, paina 5 ja siirrä sen jälkeen osoitinta painikkeilla 7 ja 8. Käytä interpolate()-funktiota laskeaksesi funktion arvot x-arvolistalle: |
|
Luettelo > |
|
|
invχ2(Ala,df) invChi2(Ala,df) Laskee käänteisen kumulatiivisen χ2 (chi-neliö) -todennäköisyysfunktion, joka on määritelty vapauden asteella, df annetulle käyrän alapuoliselle alalle Ala. |
|
|
Luettelo > |
|
|
invF(Ala,dfOsoitt,dfNimitt) vakioF(Area,dfOsoitt,dfNimitt) Laskee käänteisen kumulatiivisen F-jakaumafunktion, jolle on määritelty dfOsoitt ja dfNimitt, annetulle käyrän alapuoliselle alueelle Ala. |
|
|
Luettelo > |
|
|
invBinom(CumulativeProb,NumTrials,Prob, Käänteinen binomi. Johtuen kokeiden (NumTrials) ja kunkin kokeen todennäköisyydestä onnistua (Prob), tämä toiminto laskee onnistumisten minimimäärän, ksiten, että arvo k on suurempi tai yhtä suuri kuin kumuloituva todennäköisyys (CumulativeProb). OutputForm=0, näyttää tuloksen asteikkomuodossa (oletus). OutputForm=1, näyttää tuloksen matriisina. |
Esimerkki: Mary ja Kevin pelaavat noppapeliä. Maryn on arvattava, miten monta kertaa numero 6 enintään esiintyy 30 heittoa kohti. Jos numero 6 esiintyy yhtä monta kertaa tai vähemmän, Mary voittaa. Lisäksi, mitä pienempi on hänen arvaamansa määrä, sitä suuremmat ovat hänen voittonsa. Mikä on pienin määrä, jonka Mary voi arvata, jos hän haluaa voittamisen todennäköisyyden olevan suurempi kuin 77 %?
|
|
Luettelo > |
|
|
invBinomN(CumulativeProb,Prob, N:n suhteen käänteisesti binominen. Johtuen menestyksen todennäköisyydestä kussakin kokeessa (Prob), onnistumisten määrä (NumSuccess), tämä funktio laskee kokeiden vähimmäismäärän N siten, että arvo, N, on vähemmän tai yhtä suuri kuin annettu kumulatiivinen todennäköisyys (CumulativeProb). OutputForm=0, näyttää tuloksen asteikkomuodossa (oletus). OutputForm=1, näyttää tuloksen matriisina. |
Esimerkki: Monique harjoittelee koriin heittoa koripallossa. Hän tietää kokemuksesta, että hänen mahdollisuutensa tehdä kori on 70 %. Hän suunnittelee harjoittelevansa, kunnes hän on tehnyt 50 koria. Kuinka montaa koria hänen on yritettävä varmistaakseen, että todennäköisyys tehdä ainakin 50 koria on enemmän kuin 0,99?
|
|
Luettelo > |
|
|
invNorm(Ala[,μ[,σ]]) Laskee käänteisen kumulatiivisen normaalijakaumafunktion annetulle alalle Ala, joka on normaalijakaumakäyrän alapuolella ja jonka määräävät μ ja σ. |
|
|
Luettelo > |
|
|
invt(Ala,df) Laskee käänteisen kumulatiivisen student t -todennäköisyysfunktion, jonka määräävät vapausaste,df ja annettu alueAlakäyrän alapuolella. |
|
|
Luettelo > |
|
|
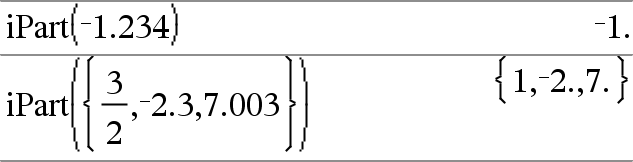
iPart(Luku) ⇒ kokonaisluku Laskee argumentin kokonaisosan. Laskee sarjoille ja matriiseille kunkin elementin kokonaisosan. Argumentti voi olla reaali- tai kompleksiluku. |
|
|
Luettelo > |
|
|
irr(CF0,CFLista [,CFFrekv]) ⇒ arvo Talouslaskentatoiminto, joka laskee investoinnin sisäisen korkokannan. CF0on kassavirta alussa aikana 0; arvon on oltava kokonaisluku. CFLista on lista kassavirtamääristä alun kassavirran CF0 jälkeen. CFFrekv on valinnainen lista, jossa kukin elementti määrää esiintymisfrekvenssin ryhmitetylle (peräkkäiselle) kassavirtamäärälle, joka on CFFrekv:n vastaava alkutekijä. Oletusarvo on 1; jos syötät arvoja, niiden on oltava positiivisia kokonaislukuja ja < 10 000. Huomaa: Katso myös mirr(), täältä. |
|
|
Luettelo > |
|
|
isPrime(Luku) ⇒ Boolen vakiolauseke Laskee totuusarvon tosi tai epätosi ilmaistakseen, onko luku kokonaisluku ≥2, joka on tasan jaollinen vain itsellään ja ykkösellä (1) Jos Luku on pitempi kuin 306 numeroa, eikä siinä ole tekijöitä ≤1021, kaava isPrime(Luku) näyttää virheilmoituksen. Huomaa esimerkkiä syöttäessäsi: Ohjeet monirivisten ohjelmien ja funktion määritysten syöttämisestä löytyvät tuotteen ohjekirjan Laskin-osiosta. |
|
|
Luettelo > |
|
|
isVoid(Muutt) ⇒ Boolen vakiolauseke Laskee totuusarvon tosi tai epätosi ilmaisten, onko argumentti tyhjä datatyyppi. Lisätietoja tyhjistä elementeistä, katso täältä. |
|