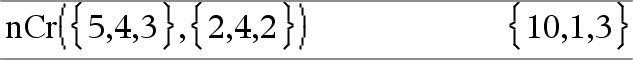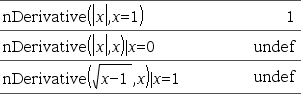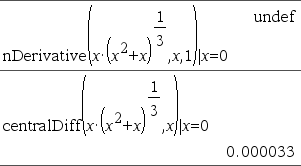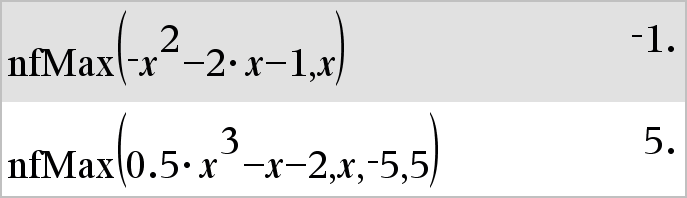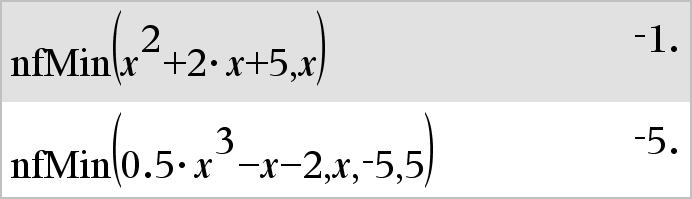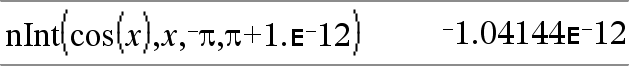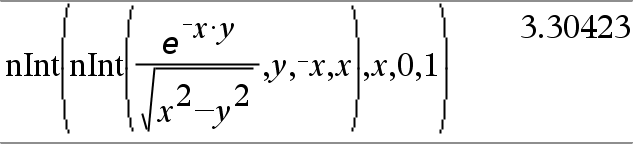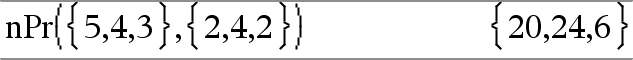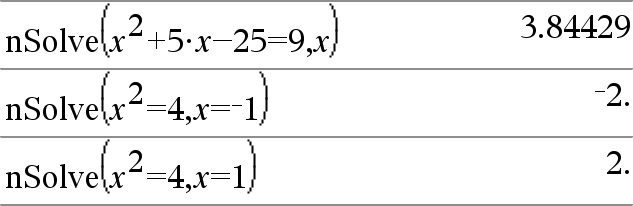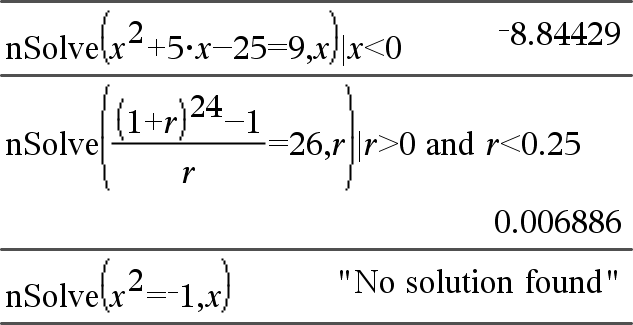|
Teclas /= |
|
|
ExprBooleana1 ListaBooleana1 MatrizBooleana1
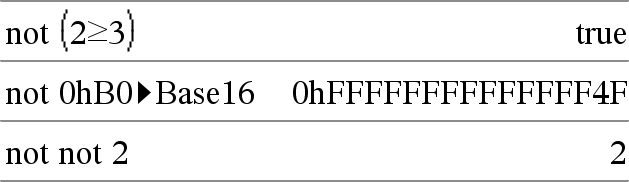
Devolve a negação de uma operação and lógica nos dois argumentos. Devolve falso, verdadeiro ou uma forma simplificada da equação. Para listas e matrizes, devolve comparações elemento por elemento. |
|
|
NúmeroInteiro1 Compara dois números inteiros reais bit a bit com uma operação Pode introduzir os números inteiros em qualquer base numérica. Para uma entrada binária ou hexadecimal, tem de utilizar o prefixo 0b ou 0h, respetivamente. Sem um prefixo, os números inteiros são tratados como decimais (base 10). |
|
|
Catálogo > |
|
|
nCr(Valor1, Valor2) Þexpressão Para o número inteiro Valor1 e Valor2 com Valor1 | Valor2 | 0, nCr() é o número de combinações de coisas de Valor1 retiradas de Valor2 de uma vez. (Isto também é conhecido como um coeficiente binomial.) nCr(Valor, 0)Þ1 nCr(Valor, NúmeroInteiroNeg)Þ0 nCr(Valor, NúmeroInteiroPos) Þ Valor ·(Valor N1)... (Valor NNúmeroInteiroPos +1)/ NúmeroInteiroPos! nCr(Valor, NúmeroNãoInteiro) Þexpressão !/
|
|
|
nCr(Lista1, Lista2) Þlista Devolve uma lista de combinações com base nos pares de elementos correspondentes nas duas listas. Os argumentos têm de ter o mesmo tamanho de listas. |
|
|
nCr(Matriz1, Matriz2) Þmatriz Devolve uma matriz de combinações com base nos pares de elementos correspondentes nas duas matrizes. Os argumentos têm de ter o mesmo tamanho de matrizes. |
|
|
Catálogo > |
|
|
Devolve a derivada numérica calculada com os métodos de diferenciação automáticos. Ao especificar o Valor, substitui qualquer atribuição de variável anterior ou qualquer substituição atual “|” para a variável. Se a variável Var não contiver um valor numérico, tem de fornecer Valor. Ordem da derivada tem de ser 1 ou 2. |
|
|
Considere o exemplo da direita. A primeira derivada de x·(x^2+x)^(1/3) em x=0 é igual a 0. No entanto, como a primeira derivada da subexpressão (x^2+x)^(1/3) está indefinida em x=0, e este valor é utilizado para calcular a derivada da expressão total, nDerivative() reporta o resultado como indefinido e apresenta uma mensagem de aviso. Se encontrar esta limitação, verifique a solução graficamente. Pode também tentar com centralDiff(). |
|
|
Catálogo > |
|
|
newLis t(ElementosNum) Þlista Devolve uma lista com uma dimensão de ElementosNum. Cada elemento é zero. |
|
|
Catálogo > |
|
|
newMa t(LinhaNum, ColunasNum) Þmatriz Devolve uma matriz de zeros com a dimensão LinhasNum por ColunasNum. |
|
|
Catálogo > |
|
|
nfMax(Expr, Var) Þvalor nfMax(Expr, Var, LimiteInferior) Þvalor nfMax(Expr, Var, LimiteInferior, LimiteSuperior) Þvalor nfMax(Expr, Var) | LimiteInferior{Var{LimiteSuperior Þvalor Devolve um valor numérico candidato da variável Var em que ocorre o máximo local de Expr. Se fornecer um LimiteInferior e um LimiteSuperior, a função procura o máximo local no intervalo fechado [LimiteInferior,LimiteSuperior]. |
|
|
Catálogo > |
|
|
nfMin(Expr, Var) Þvalor nfMin(Expr, Var, LimiteInferior) Þvalor nfMin(Expr, Var, LimiteInferior, LimiteSuperior) Þvalor nfMin(Expr, Var) | LimiteInferior{Var{LimiteSuperior Þvalor Devolve um valor numérico candidato da variável Var em que ocorre o mínimo local de Expr. Se fornecer um LimiteInferior e um LimiteSuperior, a função procura o mínimo local no intervalo fechado [LimiteInferior,LimiteSuperior]. |
|
|
Catálogo > |
|
|
nInt(Expr1, Var, Inferior, Superior) Þexpressão Se a expressão a integrar Expr1 não contiver nenhuma variável para além de Var e se Inferior e Superior forem constantes, ˆ positivo ou ˆ negativo, nInt() devolve uma aproximação de ‰(Expr1, Var, Inferior, Superior). Esta aproximação é uma média ponderada de alguns valores de amostra da expressão a integrar no intervalo Inferior <Var <Superior. |
|
|
O objectivo é obter seis dígitos significativos. O algoritmo adaptável termina quando parecer que o objectivo foi alcançado ou quando parecer improvável que as amostras adicionais produzam uma melhoria acentuada. Aparece um aviso (“Precisão questionável”) quando parecer que o objectivo não foi alcançado. |
|
|
Nest nInt() para fazer integração numérica múltipla. Os limites da integração podem depender das variáveis de integração fora dos limites. |
|
|
Catálogo > |
|
|
nom(TaxaEfectiva,CpY) Þvalor Função financeira que converte a taxa de juro efectiva anual TaxaEfectiva para uma taxa nominal, dando CpY como o número de períodos compostos por ano. TaxaEfectiva tem de ser um número real e CpY tem de ser um número real > 0. Nota: Consulte também eff(), aqui. |
|
|
Teclas /= |
|
|
ExprBooleana1
ListaBooleana1
MatrizBooleana1
Devolve a negação de uma operação Para listas e matrizes, devolve comparações elemento por elemento. |
|
|
NúmeroInteiro1
Compara dois números inteiros reais bit a bit com uma operação Pode introduzir os números inteiros em qualquer base numérica. Para uma entrada binária ou hexadecimal, tem de utilizar o prefixo 0b ou 0h, respetivamente. Sem um prefixo, os números inteiros são tratados como decimais (base 10). |
|
|
Catálogo > |
|
|
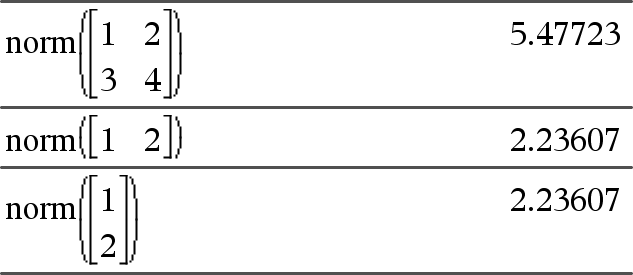
norm(Matriz)Þexpressão norm(Vector)Þexpressão Apresenta a norma Frobenius. |
|
|
Catálogo > |
|
|
normCdf(LimiteInferior,LimiteSuperior[,m[,s]])Þnúmero se LimiteInferior e LimiteSuperior forem números, lista se LimiteInferior e LimiteSuperior forem listas Calcula a probabilidade de distribuição normal entre LimiteInferior e LimiteSuperior para os m (predefinição=0) e s (predefinição=1) especificados.
|
|
|
Catálogo > |
|
|
normPdf(ValX [,m[,s]]) Þnúmero se ValX for um número, lista se ValX for uma lista Calcula a função de densidade de probabilidade para a distribuição normal num valor ValX especificado para m e s especificados. |
|
|
Catálogo > |
|
|
no t ExprBooleana ÞExpressão booleana Devolve falso, verdadeiro ou uma forma simplificada do argumento. |
|
|
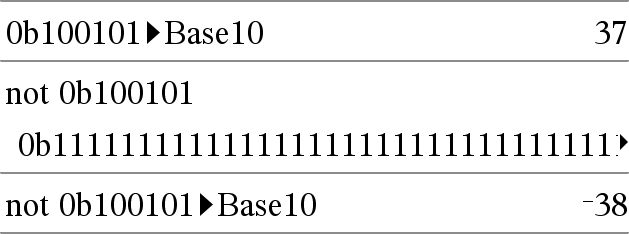
não NúmeroInteiro1 Þnúmero inteiro Devolve um complemento de um número inteiro real. Internalmente, NúmeroInteiro1 é convertido para um número de binário de 64 bits. O valor de cada bit é mudado (0 torna-se 1 e vice-versa) para um complemento. Os resultados aparecem de acordo com o modo base. Pode introduzir o número em qualquer base numérica. Para uma entrada binária ou hexadecimal, tem de utilizar o prefixo 0b ou 0h, respectivamente. Sem um prefixo, o número inteiro é tratado como decimal (base 10). Se introduzir um número inteiro na base 10 muito grande para uma forma binária de 64 bits assinada, é utilizada uma operação de módulo simétrico para colocar o valor no intervalo adequado. Para mais informações, consulte 4Base2, aqui. |
No modo base Hex: Importante: Zero, não a letra O.
No modo base Bin:
Para ver o resultado completo, prima 5 e, de seguida, utilize 7 e 8 para mover o cursor. Nota: Uma entrada binária pode ter até 64 dígitos (não contando com o prefixo 0b). Uma entrada hexadecimal pode ter até 16 dígitos. |
|
Catálogo > |
|
|
nPr(Valor1, Valor2) Þexpressão Para o número inteiro Valor1 e Valor2 com Valor1 | Valor2 | 0, nPr() é o número de permutações de coisas de Valor1 retiradas de Valor2 de uma vez. nPr(Valor, 0) Þ1 nPr(Valor, NúmeroInteiroNeg) nPr(Valor, NúmeroInteiroPos) nPr(Valor, NúmeroNãoInteiro) |
|
|
nPr(Lista1, Lista2) Þlista Devolve uma lista de permutações com base nos pares de elementos correspondentes nas duas listas. Os argumentos têm de ter o mesmo tamanho de listas. |
|
|
nPr(Matriz1, Matriz2) Þmatriz Devolve uma matriz de permutações com base nos pares de elementos correspondentes nas duas matrizes. Os argumentos têm de ter a a mesma matriz de tamanhos. |
|
|
Catálogo > |
|
|
npv(TaxaDeJuro, CFO, ListaCF [, FreqCF ]) Função financeira que calcula o valor líquido actual; a soma dos valores actuais de entradas e saídas do cash flow. Um resultado positivo para npv indica um investimento lucrativo. TaxaDeJuro é a taxa a descontar dos cash flows (o custo do dinheiro) durante um período. CF0 é o cash flow inicial no momento 0; tem de ser um número real. ListaCF é uma lista de montantes de cash flow após o cash flow inicial CF0. FreqCF é uma lista em que cada elemento especifica a frequência da ocorrência para um montante de cash flow agrupado (consecutivo), que é o elemento correspondente de ListaCF. A predefinição é 1; se introduzir valores, têm de ser números inteiros positivos < 10,000. |
|
|
Catálogo > |
|
|
nSolve(Equação, Var [= Tentativa ]) Þnúmero ou erro da cadeia nSolve(Equação, Var [= Tentativa ], LimiteInferior) Þnúmero ou erro da cadeia nSolve(Equação, Var [= Tentativa ], LimiteInferior, LimiteSuperior) Þnúmero ou erro da cadeia nSolve(Equação, Var [= Tentativa ]) | LimiteInferior{Var{LimiteSuperiorÞ número ou erro da cadeia Procura iterativamente uma solução numérica real aproximada para Equação para uma variável. Especifique a variável como: variável – ou – variável = número real Por exemplo, x é válido e logo é x=3. |
Nota: Se existirem várias soluções, pode utilizar uma tentativa para ajudar a encontrar uma solução particular. |
|
nSolve() tenta determinar se um ponto em que o residual é zero ou dois pontos relativamente próximos em que o residual tem sinais opostos e a magnitude do residual não é excessiva. Se não conseguir atingir isto com um número modesto de pontos de amostra, devolve a cadeira “nenhuma solução encontrada.” |
|