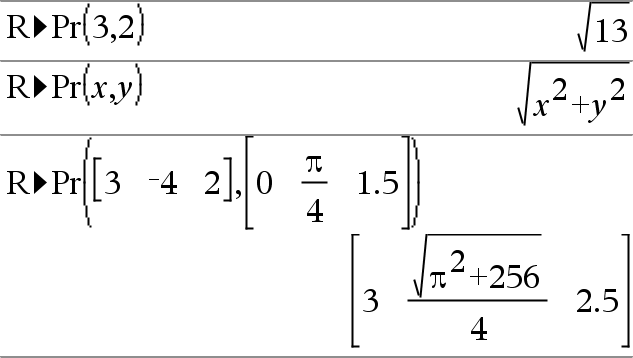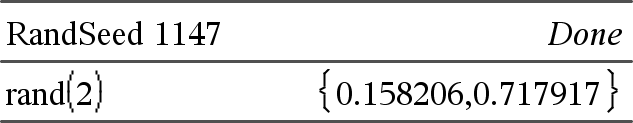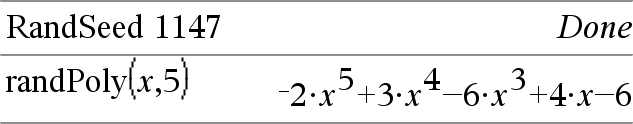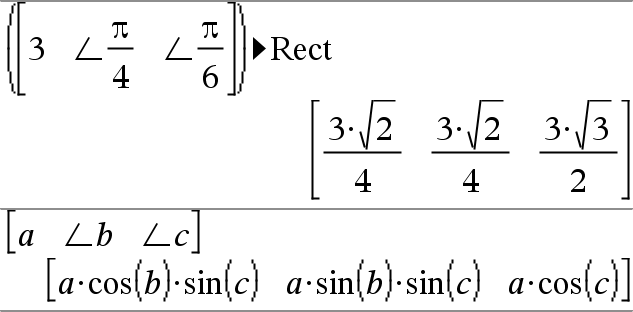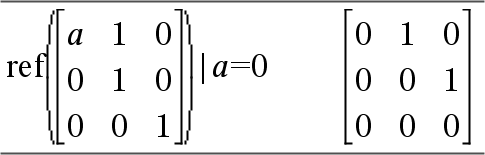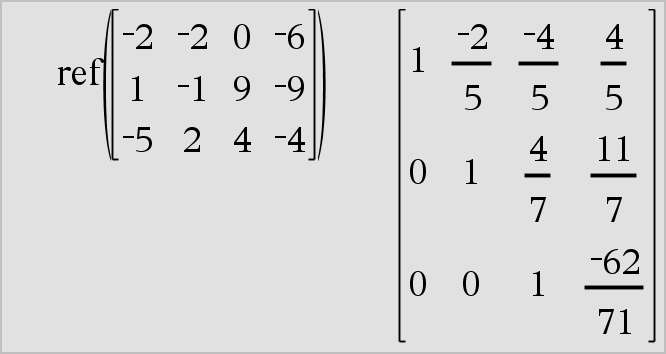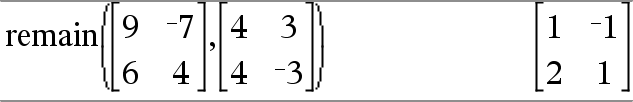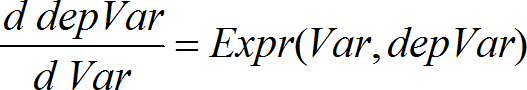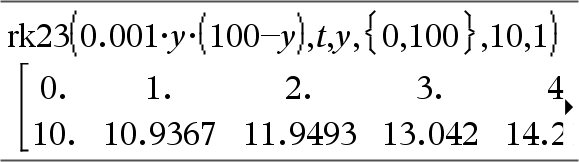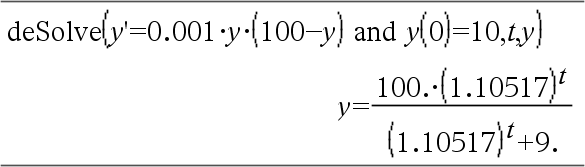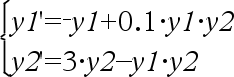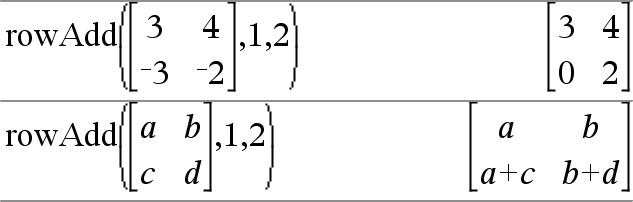R

R►Pθ()

Catalogue >

R►Pθ (xExpr, yExpr) ⇒ expression

R►Pθ (listex, listey) ⇒ liste
R►Pθ (matricex, matricey) ⇒ matrice

Donne la valeur de l'ordonnée θ - du point de coordonnées
rectangulaires (x,y).

Remarque : Donne le résultat en degrés, en grades ou en radians, suivant le mode angulaire utilisé.

Remarque : Vous pouvez insérer cette fonction à partir du clavier de l'ordinateur en entrant R@>Ptheta(...).

En mode Angle en degrés :


En mode Angle en grades :


En mode Angle en radians et en mode Auto :

R►Pr()

Catalogue >

R►Pr (xExpr, yExpr) ⇒ expression

R►Pr (listex, listey) ⇒ liste
R►Pr (matricex, matricey) ⇒ matrice

Donne la coordonnée r d'un point de coordonnées rectangulaires (x,y)

Remarque : Vous pouvez insérer cette fonction à partir du clavier de l'ordinateur en entrant R@>Pr(...).

En mode Angle en radians et en mode Auto :

►Rad

Catalogue >

Expr1►Rad ⇒ expression

Convertit l'argument en mesure d'angle en radians.

Remarque : Vous pouvez insérer cet opérateur à partir du clavier de l'ordinateur en entrant @>Rad.

En mode Angle en degrés :


En mode Angle en grades :

rand()

Catalogue >

rand() ⇒ expression
rand(#Trials) ⇒ liste

rand() donne un nombre aléatoire compris entre 0 et 1.

rand(nbreEssais) donne une liste de nombres aléatoires compris entre 0 et 1 pour le nombre d'essais nbreEssais

Réinitialise le générateur de nombres aléatoires.

randBin()

Catalogue >

randBin(n, p) ⇒ expression
randBin(n, p, #Trials) ⇒ liste

randBin(n, p ) donne un nombre aléatoire tiré d'une distribution binomiale spécifiée

randBin(n, p, nbreEssais) donne une liste de nombres aléatoires tirés d'une distribution binomiale spécifiée pour un nombre d'essais nbreEssais.

randInt()

Catalogue >

randInt(lowBound,upBound) ⇒ expression
randInt(LimiteInf,LimiteSup,NbrEssais) ⇒liste

randInt(LimiteInf,LimiteSup) donne un entier aléatoire pris entre les limites entières LimiteInf et LimiteSup

randInt(LimiteInf,LimiteSup,nbreEssais ) donne une liste d'entiers aléatoires pris entre les limites spécifiées pour un nombre d'essais nbreEssais.

randMat()

Catalogue >

randMat(nbreLignes, nbreColonnes) ⇒matrice

Donne une matrice d'entiers compris entre -9 et 9 de la dimension spécifiée.

Les deux arguments doivent pouvoir être simplifiés en entiers.

Remarque : Les valeurs de cette matrice changent chaque fois que l'on appuie sur ..

randNorm()

Catalogue >

randNorm(μ, σ) ⇒ expression
randNorm(μ, σ, nbreessais) ⇒ liste

randNorm(μ, σ) Donne un nombre décimal issu de la loi normale spécifiée. Il peut s'agir de tout nombre réel, mais le résultat obtenu sera essentiellement compris dans l'intervalle [μ−3•σ, μ+3•σ].

randNorm(μ, σ, nbreEssais) donne une liste de nombres décimaux tirés d'une distribution normale spécifiée pour un nombre d'essais nbreEssais.

randPoly()

Catalogue >

randPoly(Var, Order) ⇒ expression

Donne un polynôme aléatoire de la variable Var de degré Ordre spécifié Les coefficients sont des entiers aléatoires situés dans la plage −9 à 9. Le coefficient du terme de plus au degré (Order) sera non nul.

Ordre doit être un entier compris entre 0 et 99

randSamp()

Catalogue >

randSamp(List,#Trials[,noRepl]) ⇒ liste

Donne une liste contenant un échantillon aléatoire de nbreEssais éléments choisis dans Liste avec option de remise (sansRem=0) ou sans option de remise (sansRem=1) L'option par défaut est avec remise.

RandSeed

Catalogue >

RandSeed Nombre

Si Nombre = 0, réinitialise le générateur de nombres aléatoires Si Nombre ≠ 0, il sert à générer deux germes qui sont stockés dans les variables système seed1 et seed2

real()

Catalogue >

real(Expr1) ⇒ expression

Donne la partie réelle de l'argument.

Remarque : Toutes les variables non affectées sont considérées comme réelles. Voir également imag(), ici.

real(List1) ⇒ liste

Donne les parties réelles de tous les éléments.

real(Matrix1) ⇒ matrice

Donne les parties réelles de tous les éléments.

►Rect

Catalogue >

Vecteur ►Rect

Remarque : Vous pouvez insérer cet opérateur à partir du clavier de l'ordinateur en entrant @>Rect

Affiche Vecteur en coordonnées rectangulaires [x, y, z]. Le vecteur doit être un vecteur ligne ou colonne de dimension 2 ou 3.

Remarque : ►Rect est uniquement une instruction d'affichage et non une fonction de conversion. On ne peut l'utiliser qu'à la fin d'une ligne et elle ne modifie pas le contenu du registre ans.

Remarque : Voir également ►Polar, ici.

complexValue ►Rect

Affiche valeurComplexe sous forme rectangulaire (a+bi) La valeurComplexe peut prendre n'importe quelle forme rectangulaire Toutefois, une entrée reiθ génère une erreur en mode Angle en degrés

Remarque : Vous devez utiliser des parenthèses pour les entrées en polaire (r∠θ).

En mode Angle en radians et en modes Auto :


En mode Angle en grades :


En mode Angle en degrés :

Remarque : Pour taper ∠ à partir du clavier, sélectionnez-le dans la liste des symboles du Catalogue.

ref()

Catalogue >

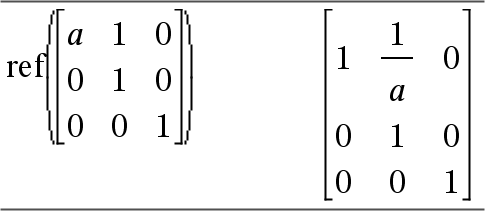
ref(Matrix1[, Tol]) ⇒ matrice

Donne une réduite de Gauss de la matrice Matrice1.

L'argument facultatif Tol permet de considérer comme nul tout élément de la matrice dont la valeur absolue est inférieure à Tol. Cet argument n'est utilisé que si la matrice contient des nombres en virgule flottante et ne contient pas de variables symbolique sans valeur affectée. Dans le cas contraire, Tol est ignoré

• Si vous utilisez /· ou définissez le mode Auto ou Approché sur Approché, les calculs sont exécutés en virgule flottante
• Si Tol est omis ou inutilisé, la tolérance par défaut est calculée comme suit :
5E−14 •max(dim(Matrice1)) •rowNorm(Matrice1)

N'utilisez pas d'éléments non définis dans Matrice1. L'utilisation d'éléments non définis peut générer des résultats inattendus.

Par exemple, si a est un élément non défini dans l'expression suivante, un message d'avertissement s'affiche et le résultat affiché est le suivant :

Un message d'avertissement est affiché car l'élément 1/a n'est pas valide pour a=0.

Pour éviter ce problème, vous pouvez stocker préalablement une valeur dans a ou utiliser l'opérateur "sachant que" (« | ») pour substituer une valeur, comme illustré dans l'exemple suivant.

Remarque : Voir également rref(), ici.

 

RefreshProbeVars

Catalogue >

RefreshProbeVars

Vous permet d’accéder aux données de capteur à partir de toutes les sondes de capteur connectées à l’aide de votre programme TI-Basic.

Valeur StatusVar

État

statusVar=0

Normal (Poursuivez le programme)

statusVar=1

L’application Vernier DataQuest™ est en mode Acquisition de données.

Remarque : L’application Vernier DataQuest™ doit être en mode compteur pour que cette commande fonctionne.

statusVar=2

L’application Vernier DataQuest™ n’est pas lancée.

statusVar=3

L’application Vernier DataQuest™ est lancée, mais vous n’avez pas encore connecté de sonde.

Par exemple

Define temp()=

Prgm

© Vérifier si le système est prêt

RefreshProbeVars status

Si le statut=0 alors

Disp "prêt"

For n,1,50

RefreshProbeVars status

température:=compteur.température

Disp "Température: ",température

Si la température>30 alors

Disp "Trop chaude"

EndIf

© Attendre pendant 1 seconde entre les échantillons

Wait 1

EndFor

Else

Disp "Pas prêt. Réessayer plus tard"

EndIf

EndPrgm

 

Remarque : Ceci peut également être utilisé avec le TI-Innovator™ Hub.

 

remain()

Catalogue >

remain(Expr1, Expr2) ⇒ expression

remain(Liste1, Liste2) ⇒ liste
remain(Matrice1, Matrice2) ⇒ matrice

Donne le reste de la division euclidienne du premier argument par le deuxième argument, défini par les identités suivantes :

remain(x,0)   x
remain(x,y)   x−y•iPart(x/y)

Par conséquent, remarquez que remain(–x,y)–remain(x,y). Le résultat peut soit être égal à zéro , soit être du même signe que le premier argument.

Remarque : Voir aussi mod(), ici.

Request

Catalogue >

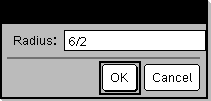
Request promptString, var[, DispFlag [, statusVar]]

Request promptString, func(arg1, ...argn)  [, DispFlag [, statusVar]]

Commande de programmation : Marque une pause dans l'exécution du programme et affiche une boîte de dialogue contenant le message chaîneinvite, ainsi qu'une zone de saisie destinée à la réponse que doit fournir l'utilisateur.

Lorsque l'utilisateur saisit une réponse et clique sur OK, le contenu de la zone de saisie est affecté à la variable var.

Si l’utilisateur clique sur Annuler, le programme continue sans accepter aucune entrée. Le programme utilise la valeur précédete de la variable var si var était déjà définie.

L'argument optionnel IndicAff peut correspondre à toute expression.

• Si IndicAff est omis ou a pour valeur 1, le message d'invite et la réponse de l'utilisateur sont affichés dans l'historique de l'application Calculs.
• Si IndicAff a pour valeur 0, le message d'invite et la réponse de l'utilisateur ne sont pas affichés dans l'historique.

Définissez un programme :

Define request_demo()=Prgm
    Request “Rayon : ”,r
    Disp “Area = “,pi*r2
EndPrgm

 

Exécutez le programme et saisissez une réponse :

request_demo()

Après avoir sélectionné OK, le résultat suivant s'affiche :

Demi-droite : 6/2
Area= 28.2743

L'argument optionnel VarÉtat indique au programme comment déterminer si l'utilisateur a fermé la boîte de dialogue. Notez que VarÉtat nécessite la saisie de l'argument IndicAff.

• Si l'utilisateur a cliqué sur OK, ou a appuyé sur Entrée ou sur Ctrl+Entrée, la variable VarÉtat prend la valeur 1.
• Sinon, la variable StatusVar prend la valeur 0.

L'argument de func() permet à un programme de stocker la réponse de l'utilisateur sous la forme d'une définition de fonction. Cette syntaxe équivaut à l'exécution par l'utilisateur de la commande suivante :

     Definir func(arg1, ...argn) = réponse de l'utilisateur

Le programme peut alors utiliser la fonction définie fonc(). La chaîneinvite doit guider l'utilisateur pour la saisie d'une réponse appropriée qui complète la définition de la fonction.

Remarque : Vous pouvez utiliser l Request commande dans un programme créé par l'utilisateur, mais pas dans une fonction.

Pour arrêter un programme qui contient une commande Request dans une boucle infinie :

• Calculatrice: Maintenez la touche c enfoncée et appuyez plusieurs fois sur ·.
• Windows® : Maintenez la touche F12 enfoncée et appuyez plusieurs fois sur Entrée.
• Macintosh® : Maintenez la touche F5 enfoncée et appuyez plusieurs fois sur Entrée.
• iPad® : L’application affiche une invite. Vous pouvez continuer à patienter ou annuler.

Remarque : Voir également RequestStr, ici.

Définissez un programme :

Define polynomial()=Prgm
    Request "Saisissez un polynôme en x :",p(x)
    Disp "Les racines réelles sont :",polyRoots(p(x),x)
EndPrgm

 

Exécutez le programme et saisissez une réponse :

polynomial()

Résultat après avoir saisi x^3+3x+1 et sélectionné OK :

Les racines réelles sont : {-0.322185}

RequestStr

Catalogue >

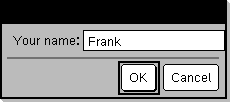
RequestStr chaîneinvite, var[, IndicAff]

Commande de programmation : Fonctionne de façon similaire à la première syntaxe de la commande Request, excepté que la réponse de l'utilisateur est toujours interprétée comme une chaîne de caractères. Par contre, la commande Request interprète la réponse comme une expression, à moins que l'utilisateur ne la saisisse entre guillemets (““).

Remarque : Vous pouvez utiliser la commande RequestStr dans un programme créé par l'utilisateur, mais pas dans une fonction.

Pour arrêter un programme qui contient une commande RequestStr dans une boucle infinie :

• Calculatrice: Maintenez la touche c enfoncée et appuyez plusieurs fois sur ·.
• Windows® : Maintenez la touche F12 enfoncée et appuyez plusieurs fois sur Entrée.
• Macintosh® : Maintenez la touche F5 enfoncée et appuyez plusieurs fois sur Entrée.
• iPad® : L’application affiche une invite. Vous pouvez continuer à patienter ou annuler.

Remarque : Voir également Request, ici.

Définissez un programme :

Define requestStr_demo()=Prgm
    RequestStr “Votre nom :”,name,0
    Disp “La réponse comporte “,dim(name),” caractères.”
EndPrgm

 

Exécutez le programme et saisissez une réponse :

requestStr_demo()

 

Après avoir sélectionné OK, le résultat affiché est le suivant (notez que si l'argument IndicAff a pour valeur 0, le message d'invite et la réponse de l'utilisateur ne s'affichent pas dans l'historique) :

 

requestStr_demo()

La réponse comporte 5 caractères.

Return

Catalogue >

Return [Expr]

Donne Expr comme résultat de la fonction S'utilise dans les blocs Func...EndFunc.

Remarque : Vous pouvez utiliser Return sans argument dans un bloc Prgm...EndPrgm pour quitter un programme

Remarque pour la saisie des données de l’exemple : Pour obtenir des instructions sur la saisie des définitions de fonction ou de programme sur plusieurs lignes, consultez la section relative à la calculatrice dans votre guide de produit.

right()

Catalogue >

right(Liste1[, Num]) ⇒ liste

Donne les Nomb éléments les plus à droite de la liste Liste1.

Si Nomb est absent, on obtient Liste1.

right(chaîneSrce[,Nomb]) ⇒chaîne

Donne la chaîne formée par les Nomb caractères les plus à droite de la chaîne de caractères chaîneSrce.

Si Nomb est absent, on obtient chaîneSrce.

right(Comparaison) ⇒ expression

Donne le membre de droite d'une équation ou d'une inéquation.

rk23 ()

Catalogue >

rk23(Expr, Var, depVar, {Var0, VarMax}, depVar0, VarStep [, diftol]) ⇒ matrice

rk23(SystemOfExpr, Var, ListOfDepVars, {Var0, VarMax}, ListOfDepVars0, VarStep[, diftol]) ⇒ matrix

rk23(ListOfExpr, Var, ListOfDepVars, {Var0, VarMax}, ListOfDepVars0, VarStep[, diftol]) ⇒ matrice

Utilise la méthode de Runge-Kutta pour résoudre le système d'équations.

with depVar(Var0)=depVar0 pour l'intervalle [Var0,VarMax]. Retourne une matrice dont la première ligne définit les valeurs de sortie de Var, définies à partir de IncVar. La deuxième ligne définit la valeur du premier composant de la solution aux valeurs Var correspondantes, etc.

Expr représente la partie droite qui définit l'équation différentielle.

SystèmeExpr correspond aux côtés droits qui définissent le système des équations différentielles (en fonction de l'ordre des variables dépendantes de la ListeVarDép).

ListeExpr est la liste des côtés droits qui définissent le système des équations différentielles (en fonction de l'ordre des variables dépendantes de la ListeVarDép).

Var est la variable indépendante.

ListeVarDép est la liste des variables dépendantes.

{Var0, MaxVar} est une liste à deux éléments qui indique la fonction à intégrer, comprise entre Var0 et MaxVar.

ListeVar0Dép est la liste des valeurs initiales pour les variables dépendantes.

Si IncVar est un nombre différent de zéro, signe(IncVar) = signe(MaxVar–Var0) et les solutions sont retournées pour Var0+i*IncVar pour tout i=0,1,2,… tel que Var0+i*IncVar soit dans [var0,MaxVar] (il est possible qu'il n'existe pas de solution en MaxVar).

si IncVar est un nombre égal à zéro, les solutions sont retournées aux valeurs Var "Runge-Kutta".

tolErr correspond à la tolérance d'erreur (valeur par défaut 0,001).

Équation différentielle :

y'=0.001*y*(100-y) et y(0)=10

Pour afficher le résultat entier, appuyez sur 5, puis utilisez les touches 7 et 8 pour déplacer le curseur.

Même équation avec TolErr définie à 1.E–6

Comparez le résultat ci-dessus avec la solution exacte CAS obtenue en utilisant deSolve() et seqGen() :


Système d'équations :

avec y1(0)=2 et y2(0)=5

root()

Catalogue >

root(Expr) ⇒ racine
root(Expr1, Expr2) ⇒ racine

root(Expr) renvoie la racine carrée de Expr.

root(Expr1, Expr2) renvoie la racine Expr2-ième de Expr1. Expr1 peut être un nombre réel ou complexe en virgule flottante, un entier ou une constante rationnelle complexe, ou une expression symbolique générale

Remarque : Voir aussi Modèle Racine n-ième, ici.

rotate()

Catalogue >

rotate(Entier1[,NbreRotations]) ⇒ entier

Permute les bits de la représentation binaire d'un entier. Vous pouvez saisir Entier1 dans un système de numération quelconque ; il est converti automatiquement en une forme binaire 64 bits signée. Si Entier1 est trop important pour être codé, il est ramené à l'aide d'une congruence dans la plage appropriée Pour plus d’informations, consultez la section ►Base2,  ici.

En mode base Bin :

 

Pour afficher le résultat entier, appuyez sur 5, puis utilisez les touches 7 et 8 pour déplacer le curseur.

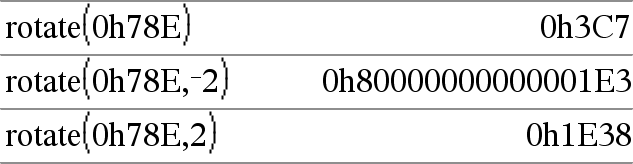
Si nbreRotations est positif, la permutation circulaire s'effectue vers la gauche Si nbreRotations est négatif, la permutation circulaire s'effectue vers la droite La valeur par défaut est −1 (permutation circulation de un bit vers la droite)

Par exemple, dans une permutation circulaire vers la droite :

En mode base Hex :

Chaque bit est permuté vers la droite.

0b00000000000001111010110000110101

Le bit le plus à droite passe à la position la plus à gauche.

donne :

0b10000000000000111101011000011010

Le résultat s'affiche suivant le mode Base utilisé.

Important : Pour une entrée binaire ou hexadécimale, vous devez utiliser respectivement le préfixe 0b ou 0h (zéro, pas la lettre O).

rotate(Liste1[,NbreRotations]) ⇒ liste

Donne une copie de Liste1 dont les éléments ont été permutés circulairement vers la gauche ou vers la droite de nbreRotations éléments Ne modifie en rien Liste1

Si nbreRotations est positif, la permutation circulaire s'effectue vers la gauche Si nbreRotations est négatif, la permutation circulaire s'effectue vers la droite. La valeur par défaut est −1 (permutation circulation de un bit vers la droite)

En mode base Dec :

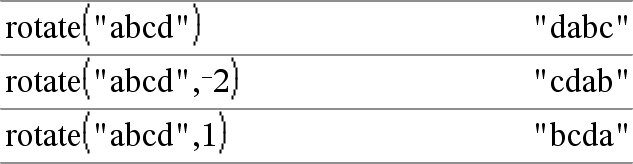
rotate(Chaîne1[,nbreRotations]) ⇒ chaîne

Donne une copie de Chaîne1 dont les caractères ont été permutés circulairement vers la gauche ou vers la droite de nbreRotations caractères. Ne modifie en rien Chaîne1

Si nbreRotations est positif, la permutation circulaire s'effectue vers la gauche Si nbreRotations est négatif, la permutation circulaire s'effectue vers la droite La valeur par défaut est −1 (permutation vers la droite d'un caractère).

round()

Catalogue >

round(Expr1[, chiffres]) ⇒ expression

Arrondit l'argument au nombre de chiffres n spécifié après la virgule.

chiffres doit être un entier compris dans la plage 0–12. Si chiffres esf absent, affiche l’argument arrondi à 12 chiffres significatifs.

Remarque : Le mode d'affichage des chiffres peut affecter le résultat affiché.

round(List1[, chiffres]) ⇒ liste

Donne la liste des éléments arrondis au nombre de chiffres spécifié.

round(Matrice1[, chiffres]) ⇒ matrice

Donne une matrice des éléments arrondis au nombre de chiffres n spécifié..

rowAdd()

Catalogue >

rowAdd(Matrice1, rIndex1, rIndex2) ⇒ matrice

Donne une copie de Matrice1 obtenue en remplaçant dans la matrice la ligne IndexL2 par la somme des lignes IndexL1 et IndexL2

rowDim()

Catalogue >

rowDim(Matrix) ⇒ expression

Donne le nombre de lignes de Matrice.

Remarque : Voir aussi colDim(), ici.

normeLig

Catalogue >

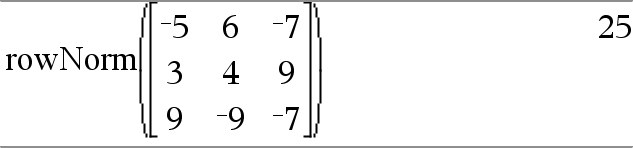
rowNorm(Matrice) ⇒ expression

Donne le maximum des sommes des valeurs absolues des éléments de chaque ligne de Matrice.

Remarque : La matrice utilisée ne doit contenir que des éléments numériques. Voir aussi colNorm() ici.

rowSwap()

Catalogue >

rowSwap(Matrice1, IndexL1, IndexL2) ⇒ matrice

Donne la matrice Matrice1 obtenue en échangeant les lignes IndexL1 et IndexL2.

rref()

Catalogue >

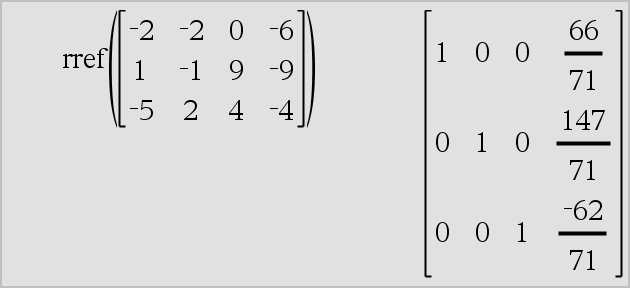
rref(Matrice1[, Tol]) ⇒ matrice

Donne la réduite de Gauss-Jordan de Matrice1.

L'argument facultatif Tol permet de considérer comme nul tout élément de la matrice dont la valeur absolue est inférieure à Tol. Cet argument n'est utilisé que si la matrice contient des nombres en virgule flottante et ne contient pas de variables symbolique sans valeur affectée. Dans le cas contraire, Tol est ignoré

• Si vous utilisez /· ou définissez le mode Auto ou Approché sur Approché, les calculs sont exécutés en virgule flottante
• Si Tol est omis ou inutilisé, la tolérance par défaut est calculée comme suit :
5E−14 •max(dim(Matrice1)) •rowNorm(Matrice1)

Remarque : Voir aussi ref() ici.