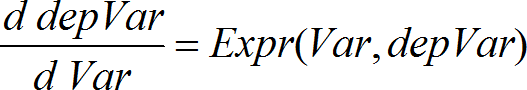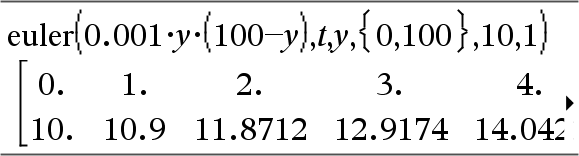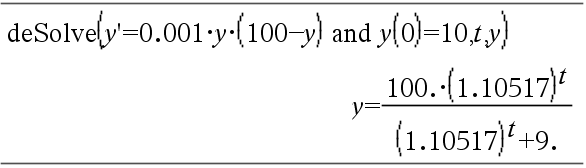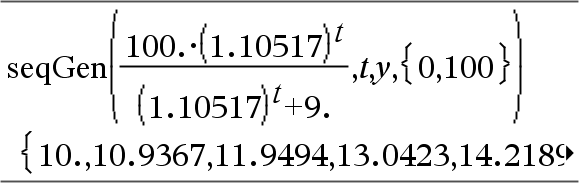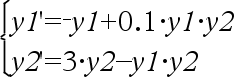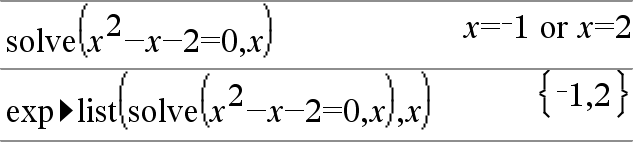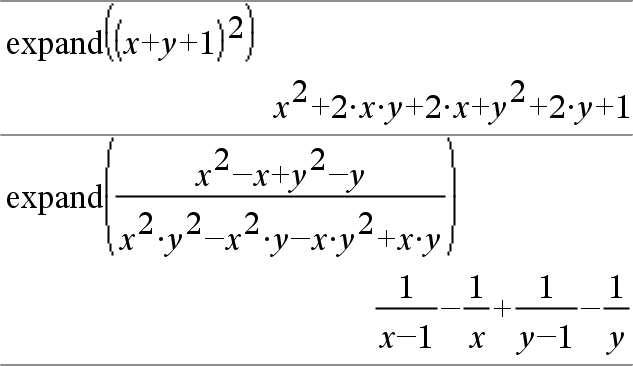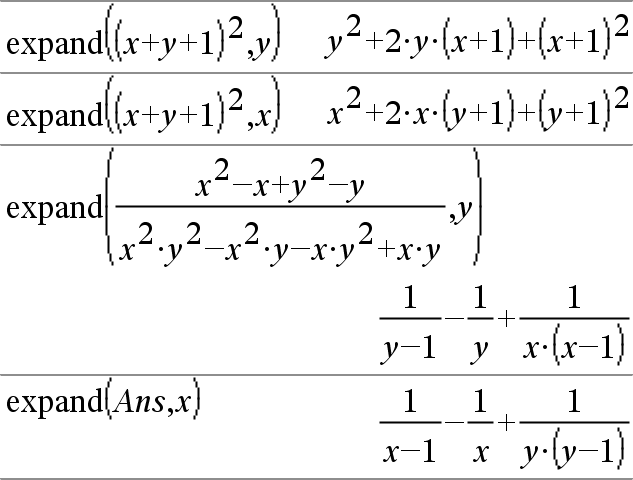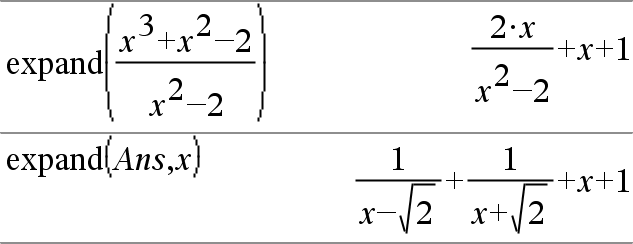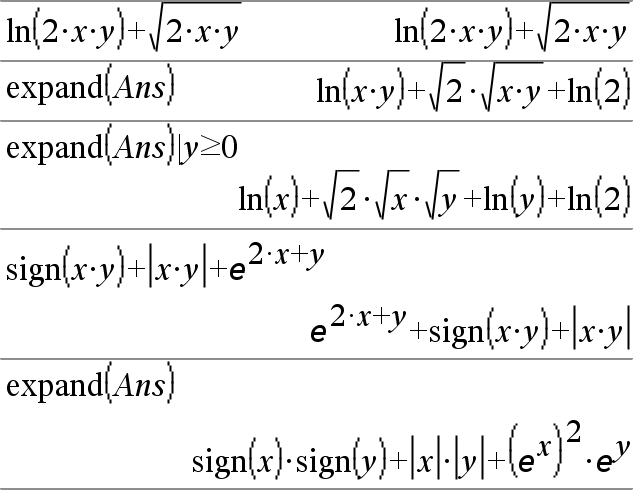|
u Taste |
|
|
e^(Ausdr1)ÞAusdruck Gibt e hoch Ausdr1 zurück. Hinweis: Siehe auch Vorlage e Exponent, hier. Hinweis: Das Drücken von u zum Anzeigen von e^( ist nicht das gleiche wie das Drücken von E auf der Tastatur. Sie können eine komplexe Zahl in der polaren Form rei q eingeben. Verwenden Sie diese aber nur im Winkelmodus Bogenmaß, da die Form im Grad- oder Neugrad-Modus einen Bereichsfehler verursacht. |
|
|
e^(Liste1)ÞListe Gibt e hoch jedes Element der Liste1 zurück. |
|
|
e^(Quadratmatrix1)ÞQuadratmatrix Ergibt den Matrix-Exponenten von Quadratmatrix1. Dies ist nicht gleichbedeutend mit der Berechnung von e hoch jedes Element. Näheres zur Berechnungsmethode finden Sie im Abschnitt cos(). Quadratmatrix1 muss diagonalisierbar sein. Das Ergebnis enthält immer Fließkommazahlen. |
|
|
Katalog > |
|
|
eff(Nominalzinssatz, CpY)ÞWert Finanzfunktion, die den Nominalzinssatz Nominalzinssatz in einen jährlichen Effektivsatz konvertiert, wobei CpY als die Anzahl der Verzinsungsperioden pro Jahr gegeben ist. Nominalzinssatz muss eine reelle Zahl sein und CpY muss eine reelle Zahl > 0 sein. Hinweis: Siehe auch nom(), hier. |
|
|
Katalog > |
|
|
eigVc(Quadratmatrix)ÞMatrix Ergibt eine Matrix, welche die Eigenvektoren für eine reelle oder komplexe Quadratmatrix enthält, wobei jede Spalte des Ergebnisses zu einem Eigenwert gehört. Beachten Sie, dass ein Eigenvektor nicht eindeutig ist; er kann durch einen konstanten Faktor skaliert werden. Die Eigenvektoren sind normiert, d. h. wenn V = [x1, x2, …, xn], dann: x12 + x22 + … + xn2 = 1 Quadratmatrix wird zunächst mit Ähnlichkeitstransformationen bearbeitet, bis die Zeilen- und Spaltennormen so nahe wie möglich bei demselben Wert liegen. Die Quadratmatrix wird dann auf die obere Hessenberg-Form reduziert, und die Eigenvektoren werden mit einer Schur-Faktorisierung berechnet. |
Im Komplex-Formatmodus “kartesisch”:
Um das ganze Ergebnis zu sehen, drücken Sie 5 und verwenden dann 7 und 8, um den Cursor zu bewegen. |
|
Katalog > |
|
|
eigVl(Quadratmatrix)ÞListe Ergibt eine Liste von Eigenwerten einer reellen oder komplexen Quadratmatrix. Quadratmatrix wird zunächst mit Ähnlichkeitstransformationen bearbeitet, bis die Zeilen- und Spaltennormen so nahe wie möglich bei demselben Wert liegen. Die Quadratmatrix wird dann auf die obere Hessenberg-Form reduziert, und die Eigenwerte werden aus der oberen Hessenberg-Matrix berechnet. |
Im Komplex-Formatmodus “kartesisch”:
Um das ganze Ergebnis zu sehen, drücken Sie 5 und verwenden dann 7 und 8, um den Cursor zu bewegen. |
|
Siehe If, hier. |
|
|
|
|
|
Katalog > |
|
|
If Boolescher Ausdr1 Then Hinweis zum Eingeben des Beispiels: Anweisungen für die Eingabe von mehrzeiligen Programm- und Funktionsdefinitionen finden Sie im Abschnitt „Calculator“ des Produkthandbuchs. |
|
|
Siehe For, hier. |
|
|
|
|
|
Siehe Func, hier. |
|
|
|
|
|
Siehe If, hier. |
|
|
|
|
|
Siehe Loop, hier. |
|
|
|
|
|
Siehe While, hier. |
|
|
|
|
|
Siehe Prgm, hier. |
|
|
|
|
|
Siehe Try, hier. |
|
|
|
|
|
Katalog > |
|
|
Verwendet die Euler-Methode zum Lösen des Systems
mit abhVar(Var0)=abhVar0 auf dem Intervall [Var0,VarMax]. Gibt eine Matrix zurück, deren erste Zeile die Ausgabewerte von Var definiert und deren zweite Zeile den Wert der ersten Lösungskomponente an den entsprechenden Var-Werten definiert usw. Ausdr ist die rechte Seite, die die gewöhnliche Differentialgleichung (ODE) definiert. AusdrSystem ist das System rechter Seiten, welche das ODE-System definieren (entspricht der Ordnung abhängiger Variablen in ListeAbhVar). AusdrListe ist eine Liste rechter Seiten, welche das ODE-System definieren (entspricht der Ordnung abhängiger Variablen in ListeAbhVar). Var ist die unabhängige Variable. ListeAbhVar ist eine Liste abhängiger Variablen. {Var0, VarMax} ist eine Liste mit zwei Elementen, die die Funktion anweist, von Var0 zu VarMax zu integrieren. ListeAbhVar0 ist eine Liste von Anfangswerten für abhängige Variablen. VarSchritt ist eine Zahl ungleich Null, sodass eulerSchritt ist eine positive ganze Zahl (standardmäßig 1), welche die Anzahl der Euler-Schritte zwischen Ausgabewerten bestimmt. Die tatsächliche von der Euler-Methode verwendete Schrittgröße ist VarSchrittàeulerSchritt. |
Differentialgleichung: y'=0.001*y*(100-y) und y(0)=10
Um das ganze Ergebnis zu sehen, drücken Sie 5 und verwenden dann 7 und 8, um den Cursor zu bewegen.
Gleichungssystem:
mit y1(0)=2 und y2(0)=5
|
|
Hub-Menü |
|
|
eval() ist nur im TI-Innovator™ Hub Befehlsargument von Programmierbefehlen Get, GetStr und Send gültig. Die Software wertet den Ausdruck Expr aus und ersetzt die Anweisung eval() mit dem Ergebnis als Zeichenfolge. Das Argument Expr muss zu einer reellen Zahl vereinfachbar sein. |
Stellen Sie das blaue Element von RGB LED auf halbe Intensität ein.
Setzen Sie das blaue Element auf AUS zurück.
Argument eval() muss zu einer reellen Zahl vereinfachbar sein.
Programm zum Einblenden des roten Elements
Führen Sie das Programm aus.
|
|
Obwohl eval() sein Ergebnis nicht anzeigt, können Sie die resultierende Hub-Zeichenfolge nach Ausführen des Befehls durch Prüfung einer beliebigen der folgenden speziellen Variablen anzeigen. iostr.SendAns Hinweis: Siehe auch Get (hier), GetStr (hier) und Send (hier). |
|
|
Katalog > |
|
|
exact(Ausdr1 [, Toleranz])ÞAusdruck exact(Liste1 [, Toleranz])ÞListe exact(Matrix1 [, Toleranz])ÞMatrix Benutzt den Rechenmodus 'Exakt' und gibt nach Möglichkeit die rationale Zahl zurück, die dem Argument äquivalent ist. Toleranz legt die Toleranz für die Umwandlung fest, wobei die Vorgabe 0 (null) ist. |
|
|
Katalog > |
|
|
Exit (Abbruch) Beendet den aktuellen For, While, oder Loop Block. Exit ist außerhalb dieser drei Schleifenstrukturen (For, While oder Loop) nicht zulässig. Hinweis zum Eingeben des Beispiels: Anweisungen für die Eingabe von mehrzeiligen Programm- und Funktionsdefinitionen finden Sie im Abschnitt „Calculator“ des Produkthandbuchs. |
Funktionslisting:
|
|
Katalog > |
|
|
Ausdr 4exp Drückt Ausdr durch die natürliche Exponentialfunktion e aus. Dies ist ein Anzeigeumwandlungsoperator. Er kann nur am Ende der Eingabezeile verwendet werden. Hinweis: Sie können diesen Operator über die Tastatur Ihres Computers eingeben, indem Sie @>exp eintippen. |
|
|
u Taste |
|
|
exp(Ausdr1)ÞAusdruck Gibt e hoch Ausdr1 zurück. Hinweis: Siehe auch Vorlage e Exponent, hier. Sie können eine komplexe Zahl in der polaren Form rei q eingeben. Verwenden Sie diese aber nur im Winkelmodus Bogenmaß, da die Form im Grad- oder Neugrad-Modus einen Bereichsfehler verursacht. |
|
|
exp(Liste1)ÞListe Gibt e hoch jedes Element der Liste1 zurück. |
|
|
exp(Quadratmatrix1)ÞQuadratmatrix Ergibt den Matrix-Exponenten von Quadratmatrix1. Dies ist nicht gleichbedeutend mit der Berechnung von e hoch jedes Element. Näheres zur Berechnungsmethode finden Sie im Abschnitt cos(). Quadratmatrix1 muss diagonalisierbar sein. Das Ergebnis enthält immer Fließkommazahlen. |
|
|
Katalog > |
|
|
exp4list(Ausdr,Var)ÞListe Untersucht Ausdr auf Gleichungen, die durch das Wort “ Hinweis: exp4list() ist für die Funktionen zeros und cZeros() unnötig, da diese direkt eine Liste von Lösungswerten zurückgeben. Sie können diese Funktion über die Tastatur Ihres Computers eingeben, indem Sie exp@>list(...) eintippen. |
|
|
Katalog > |
|
|
expand(Ausdr1 [, Var])ÞAusdruck expand(Liste1 [,Var])ÞListe expand(Matrix1 [,Var])ÞMatrix expand(Ausdr1) gibt Ausdr1 bezüglich sämtlicher Variablen entwickelt zurück. Die Entwicklung ist eine Polynomentwicklung für Polynome und eine Partialbruchentwicklung für rationale Ausdrücke. expand() versucht Ausdr1 in eine Summe und/oder eine Differenz einfacher Ausdrücke umzuformen. Dagegen versucht factor() Ausdr1 in ein Produkt und/oder einen Quotienten einfacher Faktoren umzuformen. |
|
|
expand(Ausdr1,Var) entwickelt Ausdr1 bezüglich Var. Gleichartige Potenzen von Var werden zusammengefasst. Die Terme und Faktoren werden mit Var als der Hauptvariablen sortiert. Es kann sein, dass als Nebeneffekt in gewissem Umfang eine Faktorisierung oder Entwicklung der zusammengefassten Koeffizienten auftritt. Verglichen mit dem Weglassen von Var spart dies häufig Zeit, Speicherplatz und Platz auf dem Bildschirm und macht den Ausdruck verständlicher. |
|
|
Selbst wenn es nur eine Variable gibt, kann das Einbeziehen von Var eine vollständigere Faktorisierung des Nenners, die für die Partialbruchentwicklung benutzt wird, ermöglichen. Tipp: Für rationale Ausdrücke ist propFrac() eine schnellere, aber weniger weitgehende Alternative zu expand(). Hinweis: Siehe auch comDenom() zu einem Quotienten aus einem entwickelten Zähler und entwickeltem Nenner. |
|
|
expand(Ausdr1,[Var]) vereinfacht auch Logarithmen und Bruchpotenzen ungeachtet von Var. Für weitere Zerlegungen von Logarithmen und Bruchpotenzen können Einschränkungen notwendig werden, um sicherzustellen, dass manche Faktoren nicht negativ sind. expand(Ausdr1, [Var]) vereinfacht auch Absolutwerte, sign() und Exponenten ungeachtet von Var. Hinweis: Siehe auch tExpand() zur trigonometrischen Entwicklung von Winkelsummen und -produkten. |
|
|
Katalog > |
|
|
expr(String)ÞAusdruck Gibt die in String enthaltene Zeichenkette als Ausdruck zurück und führt diesen sofort aus. |
|
|
Katalog > |
|
|
ExpReg X, Y [, [Häuf][, Kategorie, Mit]] Berechnet die exponentielle Regressiony = a·(b)xauf Listen X und Y mit der Häufigkeit Häuf. Eine Zusammenfassung der Ergebnisse wird in der Variablen stat.results gespeichert. (hier.) Alle Listen außer Mit müssen die gleiche Dimension besitzen. X und Y sind Listen von unabhängigen und abhängigen Variablen. Häuf ist eine optionale Liste von Häufigkeitswerten. Jedes Element in Häuf gibt die Häufigkeit für jeden entsprechenden Datenpunkt X und Y an. Der Standardwert ist 1. Alle Elemente müssen Ganzzahlen | 0 sein. Kategorie ist eine Liste von Kategoriecodes für die entsprechenden X und Y Daten. Mit ist eine Liste von einem oder mehreren Kategoriecodes. Nur solche Datenelemente, deren Kategoriecode in dieser Liste enthalten ist, sind in der Berechnung enthalten. Informationen zu den Auswirkungen leerer Elemente in einer Liste finden Sie unter “Leere (ungültige) Elemente” (hier). |
|
|
Ausgabevariable |
Beschreibung |
|
stat.RegEqn |
Regressionsgleichung: a·(b)x |
|
stat.a, stat.b |
Regressionskoeffizienten |
|
stat.r2 |
Koeffizient der linearen Bestimmtheit für transformierte Daten |
|
stat.r |
Korrelationskoeffizient für transformierte Daten (x, ln(y)) |
|
stat.Resid |
Mit dem exponentiellen Modell verknüpfte Residuen |
|
stat.ResidTrans |
Residuum für die lineare Anpassung der transformierten Daten. |
|
stat.XReg |
Liste der Datenpunkte in der modifizierten X List, die schließlich in der Regression mit den Beschränkungen für Häufigkeit, Kategorieliste und Mit Kategorien verwendet wurde |
|
stat.YReg |
Liste der Datenpunkte in der modifizierten Y List, die schließlich in der Regression mit den Beschränkungen für Häufigkeit, Kategorieliste und Mit Kategorien verwendet wurde |
|
stat.FreqReg |
Liste der Häufigkeiten für stat.XReg und stat.YReg |