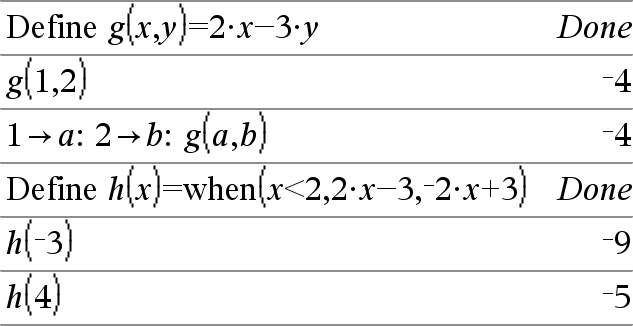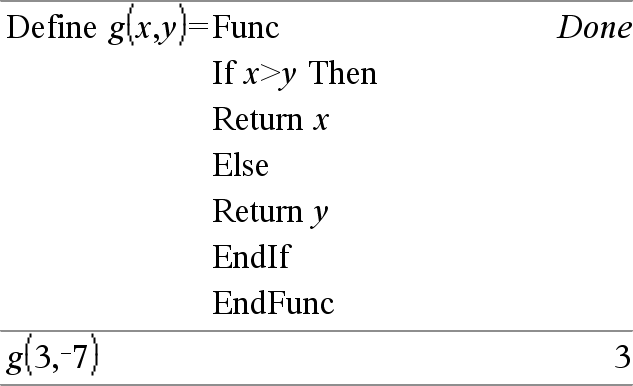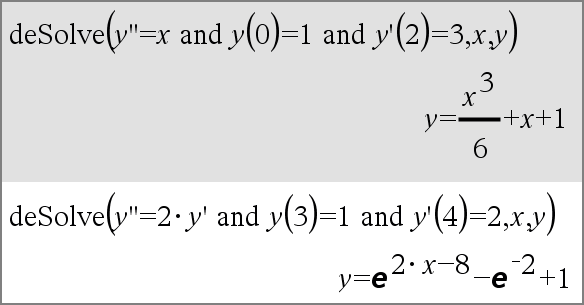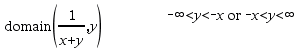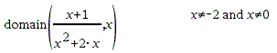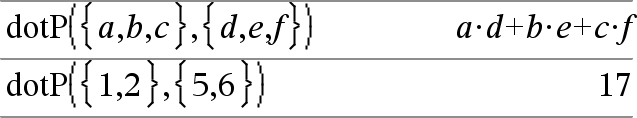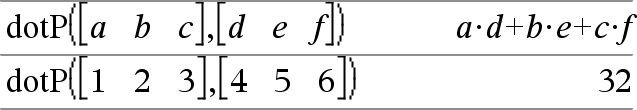dbd(Datum1,Datum2)ÞWert

Zählt die tatsächlichen Tage und gibt die Anzahl der Tage zwischen Datum1 und Datum2 zurück.

Datum1 und Datum2 können Zahlen oder Zahlenlisten innerhalb des Datumsbereichs des Standardkalenders sein. Wenn sowohl Datum1 als auch Datum2 Listen sind, müssen sie dieselbe Länge haben.

Datum1 und Datum2 müssen innerhalb der Jahre 1950 und 2049 liegen.

Sie können Datumseingaben in zwei Formaten vornehmen. Die Datumsformate unterscheiden sich in der Anordnung der Dezimalstellen.

MM.TTJJ (üblicherweise in den USA verwendetes Format)

TTMM.JJ (üblicherweise in Europa verwendetes Format)

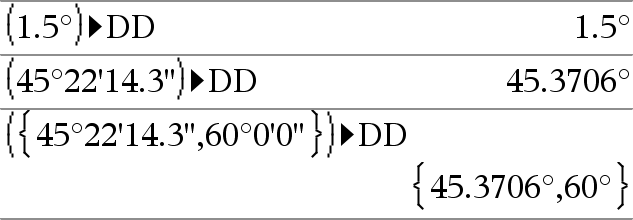
Zahl 4DDÞWert

Liste1 4DDÞListe

Matrix1 4DDÞMatrix

Hinweis: Sie können diesen Operator über die Tastatur Ihres Computers eingeben, indem Sie @>DD eintippen.

Gibt das Dezimaläquivalent des Arguments zurück. Das Argument ist eine Zahl, eine Liste oder eine Matrix, die gemäß der Moduseinstellung als Neugrad, Bogenmaß oder Grad interpretiert wird.

Ausdr1 4DecimalÞAusdruck

Liste1 4DecimalÞAusdruck

Matrix1 4DecimalÞAusdruck

Hinweis: Sie können diesen Operator über die Tastatur Ihres Computers eingeben, indem Sie @>Decimal eintippen.

Zeigt das Argument in Dezimalform an. Dieser Operator kann nur am Ende der Eingabezeile verwendet werden.

Define Function(Param1, Param2, ...) = Func
Block
EndFunc

Define Program(Param1, Param2, ...) = Prgm
Block
EndPrgm

In dieser Form kann die benutzerdefinierte Funktion bzw. das benutzerdefinierte Programm einen Block mit mehreren Anweisungen ausführen.

Block kann eine einzelne Anweisung oder eine Serie von Anweisungen in separaten Zeilen sein. Block kann auch Ausdrücke und Anweisungen enthalten (wie If, Then, Else und For).

Hinweis zum Eingeben des Beispiels: Anweisungen für die Eingabe von mehrzeiligen Programm- und Funktionsdefinitionen finden Sie im Abschnitt „Calculator“ des Produkthandbuchs.

Hinweis: Siehe auch Definiere LibPriv (Define LibPriv), hier, und Definiere LibPub (Define LibPub), hier.

Define LibPriv Var = Expression

Define LibPriv Function(Param1, Param2, ...) = Expression

Define LibPriv Function(Param1, Param2, ...) = Func
Block
EndFunc

Define LibPriv Program(Param1, Param2, ...) = Prgm
Block
EndPrgm

Funktioniert wie Define, definiert jedoch eine Variable, eine Funktion oder ein Programm für eine private Bibliothek. Private Funktionen und Programme werden im Katalog nicht angezeigt.

Hinweis: Siehe auch Definiere (Define), hier, und Definiere LibPub (Define LibPub), hier.

Define LibPub Var = Expression

Define LibPub Function(Param1, Param2, ...) = Expression

Define LibPub Function(Param1, Param2, ...) = Func
Block
EndFunc

Define LibPub Program(Param1, Param2, ...) = Prgm
Block
EndPrgm

Funktioniert wie Definiere (Define), definiert jedoch eine Variable, eine Funktion oder ein Programm für eine öffentliche Bibliothek. Öffentliche Funktionen und Programme werden im Katalog angezeigt, nachdem die Bibliothek gespeichert und aktualisiert wurde.

Hinweis: Siehe auch Definiere (Define), hier, und Definiere LibPriv (Define LibPriv), hier.

DelVar Var. löscht alle Mitglieder der Variablengruppe Var. (wie die Statistikergebnisse stat.nn oder Variablen, die mit der Funktion LibShortcut() erstellt wurden). Der Punkt (.) in dieser Form des Befehls DelVar begrenzt ihn auf das Löschen einer Variablengruppe; die einfache Variable Var ist nicht davon betroffen.

delVoid(Liste1)ÞListe

Gibt eine Liste mit dem Inhalt von Liste1 aus, wobei alle leeren (ungültigen) Elemente entfernt sind.

Weitere Informationen zu leeren Elementen finden Sie (hier).

deSolve(ODE2.OrdnungandRandbedingung1andRandbedingung2, Var, abhängigeVar)Þeine spezielle Lösung

Ergibt eine spezielle Lösung, die ODE2.Ordnung erfüllt und in zwei verschiedenen Punkten angegebene Werte aufweist.

det(Quadratmatrix[, Toleranz])ÞAusdruck

Gibt die Determinante von Quadratmatrix zurück.

Jedes Matrixelement wird wahlweise als 0 behandelt, wenn sein Absolutwert kleiner als Toleranz ist. Diese Toleranz wird nur dann verwendet, wenn die Matrix Fließkommaelemente aufweist und keinerlei symbolische Variablen ohne zugewiesene Werte enthält. Anderenfalls wird Toleranz ignoriert.

diag(Quadratmatrix)ÞZeilenmatrix

Gibt eine Zeilenmatrix zurück, die die Elemente der Hauptdiagonalen von Quadratmatrix enthält.

Quadratmatrix muss eine quadratische Matrix sein.

dim(String)ÞGanzzahl

Gibt die Anzahl der in der Zeichenkette String enthaltenen Zeichen zurück.

Disp AusdruckOderString1 [, AusdruckOderString2] ...

Zeigt die Argumente im Calculator Protokoll an. Die Argumente werden hintereinander angezeigt, dabei werden Leerzeichen zur Trennung verwendet.

Dies ist vor allem bei Programmen und Funktionen nützlich, um die Anzeige von Zwischenberechnungen zu gewährleisten.

Hinweis zum Eingeben des Beispiels: Anweisungen für die Eingabe von mehrzeiligen Programm- und Funktionsdefinitionen finden Sie im Abschnitt „Calculator“ des Produkthandbuchs.

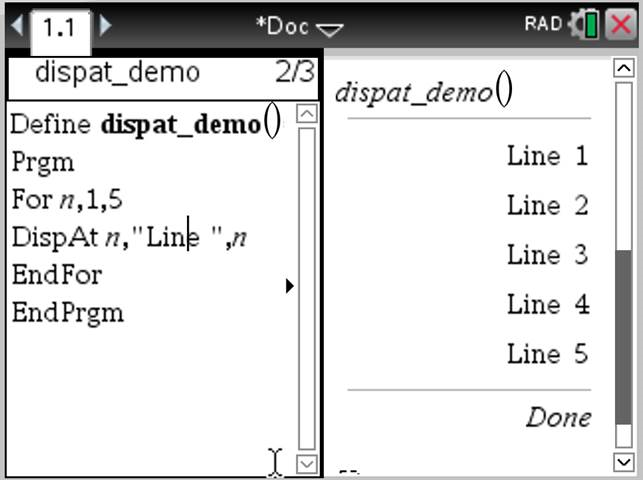
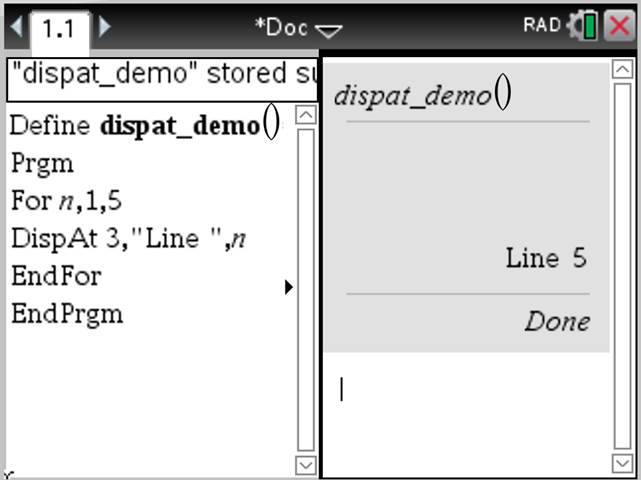
DispAt int,Term1 [,Term2 …] …

Mit DispAt können Sie die Zeile festlegen, in der der angegebene Term oder die angegebene Zeichenkette auf dem Bildschirm angezeigt wird.

Die Zeilennummer kann als Term angegeben werden.

Beachten Sie, dass die Zeilennummer nicht für den gesamten Bildschirm gedacht ist, sondern für den Bereich unmittelbar nach dem Befehl/Programm.

Dieser Befehl ermöglicht die dashboard-ähnliche Ausgabe von Programmen, bei denen der Wert eines Terms oder von einer Sensormessung in der gleichen Zeile aktualisiert wird.

DispAtund Disp können im gleichen Programm verwendet werden.

Hinweis: Die maximale Anzahl ist auf 8 eingestellt, da diese Zahl einem Bildschirm voller Zeilen auf dem Handheld-Bildschirm entspricht – soweit die Zeilen über keine mathematischen 2D-Ausdrücke verfügen. Die genaue Anzahl der Zeilen hängt vom Inhalt der angezeigten Informationen ab.

Ausdr 4DMS

Liste 4DMS

Matrix 4DMS

Hinweis: Sie können diesen Operator über die Tastatur Ihres Computers eingeben, indem Sie @>DMS eintippen.

Interpretiert den Parameter als Winkel und zeigt die entsprechenden GMS-Werte (engl. DMS) an (GGGGGG¡MM'SS.ss''). Siehe ¡, ', '' (hier) zur Erläuterung des DMS-Formats (Grad, Minuten, Sekunden).

Hinweis: 4DMS wandelt Bogenmaß in Grad um, wenn es im Bogenmaß-Modus benutzt wird. Folgt auf die Eingabe das Grad-Symbol ¡, wird keine Umwandlung vorgenommen. Sie können 4DMS nur am Ende einer Eingabezeile benutzen.

domain(Ausdr1, Var) ÞAusdruck

Gibt den Definitionsbereich von Ausdr1 in Bezug auf Var zurück.

domain() kann verwendet werden, um Definitionsbereiche von Funktionen zu erkunden. Es ist auf reelle und endliche Bereiche beschränkt.

Diese Funktionalität ist aufgrund von Schwächen von Computer-Algebra-Vereinfachungs- und Lösungsalgorithmen eingeschränkt.

Bestimmte Funktionen können nicht als Argumente für domain() verwendet werden, unabhängig davon, ob sie explizit oder innerhalb von benutzerdefinierten Variablen und Funktionen auftreten. In dem folgenden Beispiel kann der Ausdruck nicht vereinfacht werden weil ‰() eine nicht zulässige Funktion ist.

dominantTerm(Expr1, Var [, Point])Þexpression

dominantTerm(Expr1, Var [, Point]) | Var>Point  Þexpression

dominantTerm(Expr1, Var [, Point]) | Var<Point  Þexpression

Gibt den dominanten Term einer Potenzreihendarstellung von Expr1 entwickelt um Point zurück. Der dominante Term ist derjenige, dessen Betrag nahe Var = Point am schnellsten anwächst. Die resultierende Potenz von (Var N Point) kann einen negativen und/oder Bruchexponenten haben. Der Koeffizient dieser Potenz kann Logarithmen von (Var N Point) und andere Funktionen von Var enthalten, die von allen Potenzen von (Var N Point) dominiert werden, die dasselbe Exponentenzeichen haben.

Point ist vorgegeben als 0. Point kann ˆ oder Nˆ sein; in diesen Fällen ist der dominante Term eher derjenige mit dem größten Exponenten von Var als der mit dem kleinsten Exponenten von Var.

dominantTerm(…) gibt “dominantTerm(…)” zurück, wenn es keine Darstellung bestimmen kann wie für wesentliche Singularitäten wie z.B. sin(1/z) bei z=0, eN1/z bei z=0 oder ez bei z = ˆ oder Nˆ.

Wenn die Folge oder eine ihrer Ableitungen eine Sprungstelle bei Point hat, enthält das Ergebnis wahrscheinlich Unterausdrücke der Form sign(…) oder abs(…) für eine reelle Expansionsvariable oder (-1)floor(…angle(…)…) für eine komplexe Expansionsvariable, die mit “_” endet. Wenn Sie beabsichtigen, den dominanten Term nur für Werte auf einer Seite von Point zu verwenden, hängen Sie an dominantTerm(...) je nach Bedarf “| Var > Point”, “| Var < Point”, “| “Var | Point” oder “Var { Point” an, um ein einfacheres Ergebnis zu erhalten.

dominantTerm() wird über Listen und Matrizen mit erstem Argument verteilt.

dominantTerm() können Sie verwenden, wenn Sie den einfachsten möglichen Ausdruck wissen möchten, der asymptotisch zu einem anderen Ausdruck wie Var " Point ist. dominantTerm() ist ebenfalls hilfreich, wenn nicht klar ersichtlich ist, welchen Grad der erste Term einer Folge haben wird, der nicht Null ist und Sie nicht iterativ interaktiv oder mit einer Programmschleife schätzen möchten.

Hinweis: Siehe auch series(), hier.

dotP(Vektor1, Vektor2)ÞAusdruck

Gibt das Skalarprodukt zweier Vektoren zurück.

Es müssen beide Zeilenvektoren oder beide Spaltenvektoren sein.