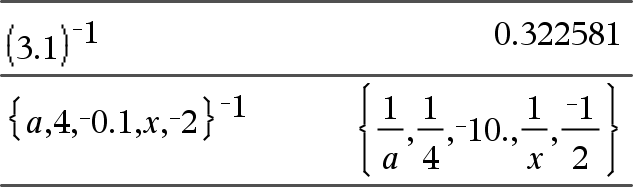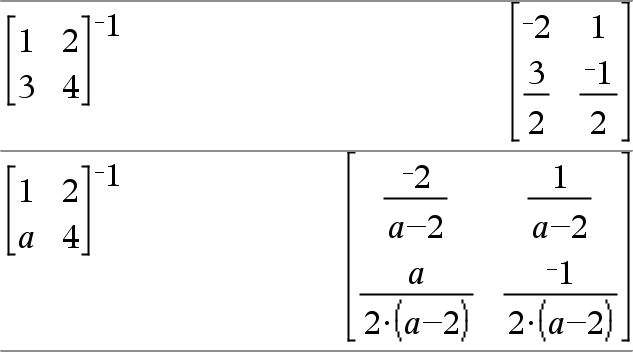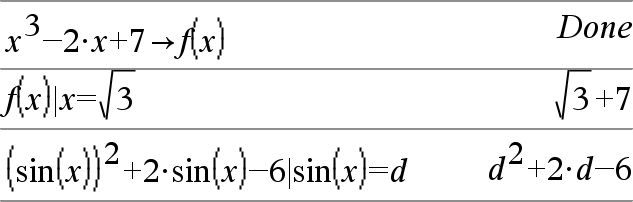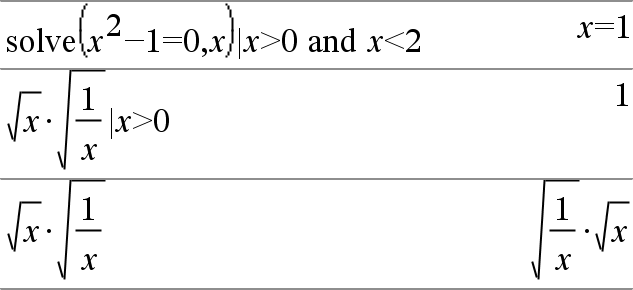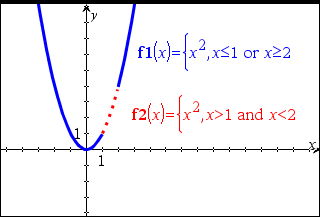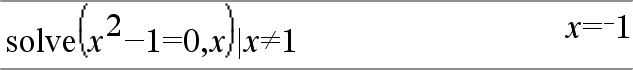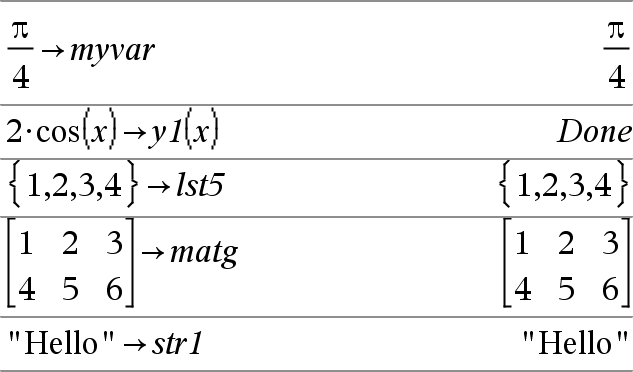|
+Taste |
|
|
Gibt die Summe der beiden Argumente zurück. |
|
|
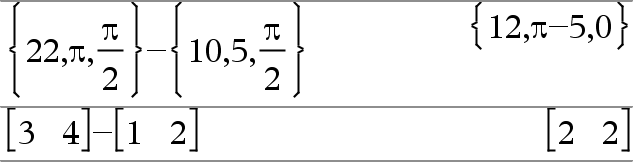
Liste1 + Liste2ÞListe Matrix1 + Matrix2ÞMatrix Gibt eine Liste (bzw. eine Matrix) zurück, die die Summen der entsprechenden Elemente von Liste1 und Liste2 (oder Matrix1 und Matrix2) enthält. Die Argumente müssen die gleiche Dimension besitzen. |
|
|
Liste1 + AusdrÞListe Gibt eine Liste zurück, die die Summen von Ausdr plus jedem Element der Liste1 enthält. |
|
|
Matrix1 + AusdrÞMatrix Gibt eine Matrix zurück, in der Ausdr zu jedem Element der Diagonalen von Matrix1 addiert ist. Matrix1 muss eine quadratische Matrix sein. Hinweis: Verwenden Sie .+ (Punkt Plus) zum Addieren eines Ausdrucks zu jedem Element. |
|
|
-Taste |
|
|
Gibt Ausdr1 minus Ausdr2 zurück. |
|
|
Liste1 N Liste2ÞListe Matrix1 N Matrix2ÞMatrix Subtrahiert die einzelnen Elemente aus Liste2 (oder Matrix2) von denen in Liste1 (oder Matrix1) und gibt die Ergebnisse zurück. Die Argumente müssen die gleiche Dimension besitzen. |
|
|
Liste1 N AusdrÞListe Subtrahiert jedes Element der Liste1 von Ausdr oder subtrahiert Ausdr von jedem Element der Liste1 und gibt eine Liste der Ergebnisse zurück. |
|
|
Matrix1 N AusdrÞMatrix Ausdr N Matrix1 gibt eine Matrix zurück, die Ausdr multipliziert mit der Einheitsmatrix minus Matrix1 ist. Matrix1 muss eine quadratische Matrix sein. Matrix1 N Ausdr gibt eine Matrix zurück, die Ausdr multipliziert mit der Einheitsmatrix subtrahiert von Matrix1 ist. Matrix1 muss eine quadratische Matrix sein. Hinweis: Verwenden Sie .N (Punkt Minus) zum Subtrahieren eines Ausdrucks von jedem Element. |
|
|
rTaste |
|
|
Gibt das Produkt der beiden Argumente zurück. |
|
|
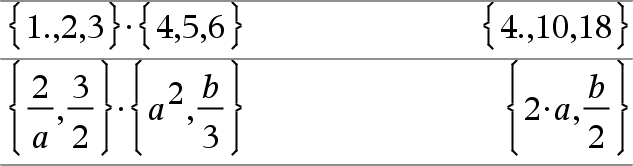
Liste1•Liste2ÞListe Gibt eine Liste zurück, die die Produkte der entsprechenden Elemente aus Liste1 und Liste2 enthält. Die Listen müssen die gleiche Dimension besitzen. |
|
|
Matrix1•Matrix2ÞMatrix Gibt das Matrizenprodukt von Matrix1 und Matrix2 zurück. Die Spaltenanzahl von Matrix1 muss gleich die Zeilenanzahl von Matrix2 sein. |
|
|
Liste1•AusdrÞListe Gibt eine Liste zurück, die die Produkte von Ausdr und jedem Element der Liste1 enthält. |
|
|
Matrix1•AusdrÞMatrix Gibt eine Matrix zurück, die die Produkte von Ausdr und jedem Element der Matrix1 enthält. Hinweis: Verwenden Sie .·(Punkt-Multiplikation) zum Multiplizieren eines Ausdrucks mit jedem Element. |
|
|
pTaste |
|
|
Gibt Ausdr1 dividiert durch Ausdr2 zurück. Hinweis: Siehe auch Vorlage Bruch, hier. |
|
|
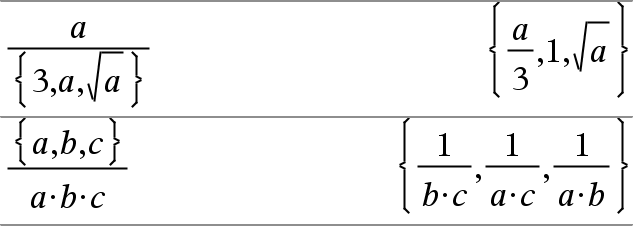
Liste1 ⁄ Liste2ÞListe Gibt eine Liste der Elemente von Liste1 dividiert durch Liste2 zurück. Die Listen müssen die gleiche Dimension besitzen. |
|
|
Liste1 à Ausdr Þ Liste Gibt eine Liste der Elemente von Ausdr dividiert durch Liste1 oderListe1 dividiert durch Ausdr zurück. |
|
|
Gibt eine Matrix zurück, die die Quotienten Matrix1àAusdr enthält. Hinweis: Verwenden Sie . / (Punkt-Division) zum Dividieren eines Ausdrucks durch jedes Element. |
|
|
l Taste |
|
|
Liste1 ^ Liste2 Þ Liste Gibt das erste Argument hoch dem zweiten Argument zurück. Hinweis: Siehe auch Vorlage Exponent, hier. Bei einer Liste wird jedes Element aus Liste1 hoch dem entsprechenden Element aus Liste2 zurückgegeben. Im reellen Bereich benutzen Bruchpotenzen mit gekürztem ungeradem Nenner den reellen statt den Hauptzeig im komplexen Modus. |
|
|
Gibt Ausdr hoch den Elementen von Liste1 zurück. |
|
|
Gibt die Elemente von Liste1 hoch Ausdr zurück. |
|
|
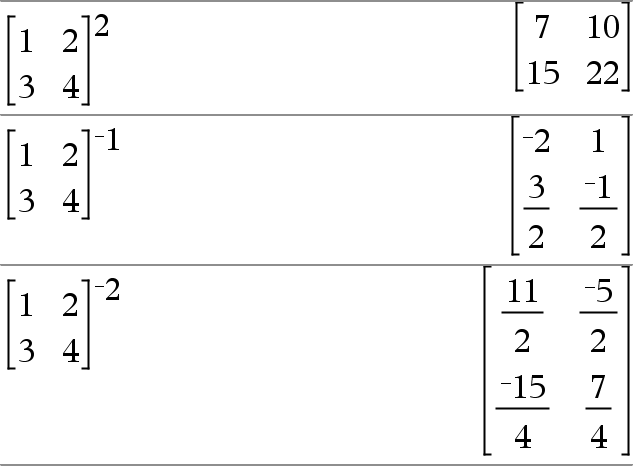
Quadratmatrix1 ^ Ganzzahl Þ Matrix Gibt Quadratmatrix1 hoch Ganzzahl zurück. Quadratmatrix1 muss eine quadratische Matrix sein. Ist Ganzzahl = L1, wird die inverse Matrix berechnet. Ist Ganzzahl < L1, wird die inverse Matrix hoch der entsprechenden positiven Zahl berechnet. |
|
|
q Taste |
|
|
Gibt das Quadrat des Arguments zurück. Liste12 Þ Liste Gibt eine Liste zurück, die die Produkte der Elemente in Liste1 enthält. Quadratmatrix12 Þ Matrix Gibt das Matriz-Quadrat von Quadratmatrix1 zurück. Dies ist nicht gleichbedeutend mit der Berechnung des Quadrats jedes einzelnen Elements. Verwenden Sie .^2, um das Quadrat jedes einzelnen Elements zu berechnen. |
|
|
^+Tasten |
|
|
Matrix1 .+ Matrix2 Þ Matrix Matrix1 .+ Matrix2 gibt eine Matrix zurück, die Summe jedes Elementpaars von Matrix1 und Matrix2 ist.
|
|
|
^-Tasten |
|
|
Matrix1 .N Matrix2 Þ Matrix Matrix1 .NMatrix2 gibt eine Matrix zurück, die die Differenz jedes Elementpaars von Matrix1 und Matrix2 ist.
|
|
|
^rTasten |
|
|
Matrix1 .· Matrix2 Þ Matrix
Matrix1 .· Matrix2 gibt eine Matrix zurück, die das Produkt jedes Elementpaars von Matrix1 und Matrix2 ist.
|
|
|
^p Tasten |
|
|
Matrix1 . / Matrix2 Þ Matrix
Matrix1 . / Matrix2 gibt eine Matrix zurück, die der Quotient jedes Elementpaars von Matrix1 und Matrix2 ist.
|
|
|
^l Tasten |
|
|
Matrix1 .^ Matrix2 Þ Matrix
Matrix1 .^ Matrix2 gibt eine Matrix zurück, in der jedes Element aus Matrix2 Exponent des entsprechenden Elements aus Matrix1 ist.
|
|
|
v Taste |
|
|
L
LListe1 Þ Liste LMatrix1 Þ Matrix Gibt die Negation des Arguments zurück. Bei einer Liste oder Matrix werden alle Elemente negiert zurückgegeben. Ist das Argument eine binäre oder hexadezimale ganze Zahl, ergibt die Negation das Zweierkomplement. |
Im Bin-Modus:
Wichtig: Null, nicht Buchstabe O
Um das ganze Ergebnis zu sehen, drücken Sie 5 und verwenden dann 7 und 8, um den Cursor zu bewegen. |
|
/k Tasten |
|
|
Liste1 % Þ Liste Matrix1 % Þ Matrix Ergibt Bei einer Liste oder einer Matrix wird eine Liste/Matrix zurückgegeben, in der jedes Element durch 100 dividiert ist. |
Hinweis: Erzwingen eines Näherungsergebnisses, Handheld: Drücken Sie / ·.
|
|
= Taste |
|
|
Ausdr1 = Ausdr2ÞBoolescher Ausdruck Liste1 = Liste2Þ Boolesche Liste Matrix1 = Matrix2Þ Boolesche Matrix Gibt wahr zurück, wenn Ausdr1 bei Auswertung gleich Ausdr2 ist. Gibt falsch zurück, wenn Ausdr1 bei Auswertung ungleich Ausdr2 ist. In allen anderen Fällen wird eine vereinfachte Form der Gleichung zurückgegeben. Bei Listen und Matrizen werden die Ergebnisse des Vergleichs der einzelnen Elemente zurückgegeben. Hinweis zum Eingeben des Beispiels: Anweisungen für die Eingabe von mehrzeiligen Programm- und Funktionsdefinitionen finden Sie im Abschnitt „Calculator“ des Produkthandbuchs. |
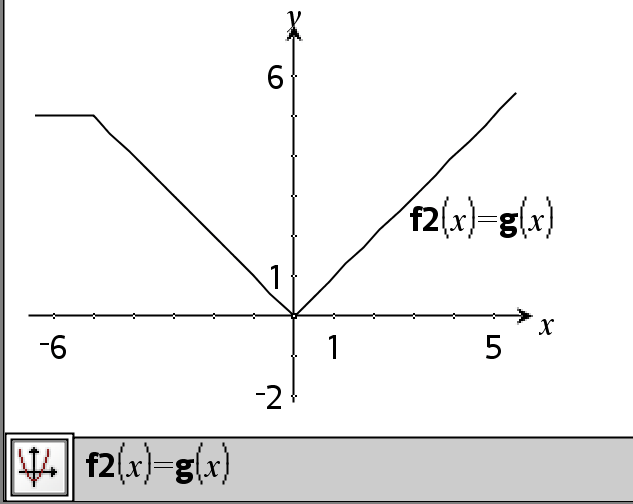
Beispielfunktion mit den mathematischen Vergleichssymbolen: =, ƒ, <, {, >, |
Ergebnis der graphischen Darstellung g(x)
|
|
/= Tasten |
|
|
Ausdr1 ƒ Ausdr2 Þ Boolescher Ausdruck Liste1 ƒ Liste2 Þ Boolesche Liste Matrix1 ƒ Matrix2 Þ Boolesche Matrix Gibt wahr zurück, wenn Ausdr1 bei Auswertung ungleich Ausdr2 ist. Gibt falsch zurück, wenn Ausdr1 bei Auswertung gleich Ausdr2 ist. In allen anderen Fällen wird eine vereinfachte Form der Gleichung zurückgegeben. Bei Listen und Matrizen werden die Ergebnisse des Vergleichs der einzelnen Elemente zurückgegeben. Hinweis: Sie können diesen Operator über die Tastatur Ihres Computers eingeben, indem Sie /= eintippen |
Siehe Beispiel bei “=” (gleich). |
|
/= Tasten |
|
|
Ausdr1 < Ausdr2 Þ Boolescher Ausdruck Liste1 < Liste2 Þ Boolesche Liste Matrix1 < Matrix2 Þ Boolesche Matrix Gibt wahr zurück, wenn Ausdr1 bei Auswertung kleiner als Ausdr2 ist. Gibt falsch zurück, wenn Ausdr1 bei Auswertung größer oder gleich Ausdr2 ist. In allen anderen Fällen wird eine vereinfachte Form der Gleichung zurückgegeben. Bei Listen und Matrizen werden die Ergebnisse des Vergleichs der einzelnen Elemente zurückgegeben. |
Siehe Beispiel bei “=” (gleich). |
|
/= Tasten |
|
|
Ausdr1 { Ausdr2 Þ Boolescher Ausdruck Liste1 { Liste2 Þ Boolesche Liste Matrix1 { Matrix2 Þ Boolesche Matrix Gibt wahr zurück, wenn Ausdr1 bei Auswertung kleiner oder gleich Ausdr2 ist. Gibt falsch zurück, wenn Ausdr1 bei Auswertung größer als Ausdr2 ist. In allen anderen Fällen wird eine vereinfachte Form der Gleichung zurückgegeben. Bei Listen und Matrizen werden die Ergebnisse des Vergleichs der einzelnen Elemente zurückgegeben. Hinweis: Sie können diesen Operator über die Tastatur Ihres Computers eingeben, indem Sie das Tastenkürzel <= |
Siehe Beispiel bei “=” (gleich). |
|
/= Tasten |
|
|
Ausdr1 > Ausdr2 Þ Boolescher Ausdruck Liste1 > Liste2 Þ Boolesche Liste Matrix1 > Matrix2 Þ Boolesche Matrix Gibt wahr zurück, wenn Ausdr1 bei Auswertung größer als Ausdr2 ist. Gibt falsch zurück, wenn Ausdr1 bei Auswertung kleiner oder gleich Ausdr2 ist. In allen anderen Fällen wird eine vereinfachte Form der Gleichung zurückgegeben. Bei Listen und Matrizen werden die Ergebnisse des Vergleichs der einzelnen Elemente zurückgegeben. |
Siehe Beispiel bei “=” (gleich). |
|
/= Tasten |
|
|
Ausdr1 | Ausdr2 Þ Boolescher Ausdruck Liste1 | Liste2 Þ Boolesche Liste Matrix1 | Matrix2 Þ Boolesche Matrix Gibt wahr zurück, wenn Ausdr1 bei Auswertung größer oder gleich Ausdr2 ist. Gibt falsch zurück, wenn Ausdr1 bei Auswertung kleiner oder gleich Ausdr2 ist. In allen anderen Fällen wird eine vereinfachte Form der Gleichung zurückgegeben. Bei Listen und Matrizen werden die Ergebnisse des Vergleichs der einzelnen Elemente zurückgegeben. Hinweis: Sie können diesen Operator über die Tastatur Ihres Computers eingeben, indem Sie das Tastenkürzel >= |
Siehe Beispiel bei “=” (gleich). |
|
/= Tasten |
|
|
BoolescherAusd1 Þ BoolescherAusdr2 ergibt Boolescher Ausdruck BoolescheListe1 Þ BoolescheLiset2 ergibt Boolesche Liste BoolescheMatrix1 Þ BoolescheMatrix2 ergibt Boolesche Matrix Ganzzahl1 Þ Ganzzahl2 ergibt Ganzzahl
Wertet den Ausdruck Bei Listen und Matrizen werden die Ergebnisse des Vergleichs der einzelnen Elemente zurückgegeben Hinweis: Sie können diesen Operator über die Tastatur Ihres Computers eingeben, indem Sie das Tastenkürzel => |
|
|
/= Tasten |
|
|
BoolescherAusdr1 Û BoolescherAusdr2 ergibt Boolescher Ausdruck BoolescheListe1 Û BoolescheLiset2 ergibt Boolesche Liste BoolescheMatrix1 Û BoolescheMatrix2 ergibt Boolesche Matrix Ganzzahl1 Û Ganzzahl2 ergibt Ganzzahl
Gibt die Negation einer Bei Listen und Matrizen werden die Ergebnisse des Vergleichs der einzelnen Elemente zurückgegeben. Hinweis: Sie können diesen Operator über die Tastatur Ihres Computers eingeben, indem Sie <=> drücken |
|
|
º Taste |
|
|
Liste1! Þ Liste Matrix1! Þ Matrix Gibt die Fakultät des Arguments zurück. Bei Listen und Matrizen wird eine Liste/Matrix mit der Fakultät der einzelnen Elemente zurückgegeben. |
|
|
& |
/k Tasten |
|
String1 & String2 Þ String Gibt einen String zurück, der durch Anfügen von String2 an String1 gebildet wurde. |
|
|
Katalog > |
||||||||||
|
d(Ausdr1, Var[, Ordnung])ÞAusdruck d(Liste1, Var[, Ordnung])ÞListe d(Matrix1, Var[, Ordnung])ÞMatrix Gibt die erste Ableitung des ersten Arguments bezüglich der Variablen Var zurück. Ordnung (sofern angegeben) muss eine ganze Zahl sein. Ist die Ordnung kleiner als Null, ist das Ergebnis eine Anti-Ableitung (Integration). Hinweis: Sie können diese Funktion über die Tastatur Ihres Computers eingeben, indem Sie
Wenn die Variable aus Schritt 1 einen gespeicherten Wert oder einen Wert hat, der durch den womit-Operator („|“) spezifiziert ist, wird dieser Wert im Ergebnis aus Schritt 3 ersetzt. Hinweis: Siehe auch Erste Ableitung, hier; Zweite Ableitung, hier; und n-te Ableitung, hier. |
|
|
Katalog > |
|
|
‰(Ausdr1, Var[, Untere, Obere]) Þ Ausdruck ‰(Ausdr1, Var[, Konstante]) Þ Ausdruck Gibt das Integral von Ausdr1 bezüglich der Variablen Var von Untere bis Obere zurück. Hinweis: Siehe auch Vorlage Bestimmtes Integral und Vorlage Unbestimmtes Integral, hier. Hinweis: Sie können diese Funktion über die Tastatur Ihres Computers eingeben, indem Sie Integral(...) eintippen. |
|
|
Gibt ein unbestimmtes Integral zurück, wenn UntGreenze und ObGreenze nicht angegeben werden. Eine symbolische Integrationskonstante wird weggelassen, sofern Sie nicht das Argument Konstante einfügen. |
|
|
Gleichwertig gültige unbestimmte Integrale können durch eine numerische Konstante voneinander abweichen. Eine solche Konstante kann verborgen sein - insbesondere, wenn ein unbestimmtes Integral logarithmische oder inverse trigonometrische Funktionen enthält. Außerdem werden manchmal stückweise konstante Ausdrücke hinzugefügt, um einem unbestimmten Integral über ein größeres Intervall Gültigkeit zu verleihen als bei der üblichen Formel. |
|
|
‰() gibt sich selbst zurück bei Stücken von Ausdr1, die es nicht als explizite endliche Kombination seiner integrierten Funktionen und Operatoren bestimmen kann. Sind sowohl UntGreenze als auch ObGreenze angegeben, wird versucht, Unstetigkeiten oder unstetige Ableitungen im Intervall UntGreenze < Var < ObGreenze zu finden, um das Intervall an diesen Stellen unterteilen zu können. |
|
|
Ist der Modus Auto oder Näherung auf Auto eingestellt, wird eine numerische Integration vorgenommen, wo dies möglich ist, wenn kein unbestimmtes Integral oder kein Grenzwert ermittelt werden kann. |
|
|
Bei der Einstellung Approximiert wird die numerische Integration, wo möglich, zuerst versucht. Unbestimmte Integrale werden nur dann gesucht, wenn die numerische Integration unzulässig ist oder fehlschlägt. |
Hinweis: Erzwingen eines Näherungsergebnisses, Handheld: Drücken Sie / ·.
|
|
‰() können verschachtelt werden, um Mehrfach-Integrale zu bearbeiten. Die Integrationsgrenzen können von außerhalb liegenden Integrationsvariablen abhängen. Hinweis: Siehe auch nInt(), hier. |
|
|
/q Tasten |
|
|
‡
‡ (Liste1)ÞListe Gibt die Quadratwurzel des Arguments zurück. Bei einer Liste wird die Quadratwurzel für jedes Element von Liste1 zurückgegeben. Hinweis: Sie können diese Funktion über die Tastatur Ihres Computers eingeben, indem Sie sqrt(...) eintippen. Hinweis: Siehe auch Vorlage Quadratwurzel, hier. |
|
|
Katalog > |
|
|
P(Ausdr1, Var, Von, Bis)ÞAusdruck Hinweis: Sie können diese Funktion über die Tastatur Ihres Computers eingeben, indem Sie prodSeq(...) eintippen. Wertet Ausdr1 für jeden Wert von Var zwischen Von und Bis aus und gibt das Produkt der Ergebnisse zurück. Hinweis: Siehe auch Vorlage Produkt (P), hier. |
|
|
P(Ausdr1, Var, Von, VonN1)Þ1 P(Ausdr1, Var, Von, Bis) Þ1/P(Ausdr1, Var, Bis+1, VonN1) if Bis < VonN1
Die verwendeten Produktformeln wurden ausgehend von der folgenden Quelle entwickelt: Ronald L. Graham, Donald E. Knuth, Oren Patashnik: Concrete Mathematics: A Foundation for Computer Science. Reading, Massachusetts: Addison-Wesley 1994. |
|
|
Katalog > |
|
|
G(Ausdr1, Var, Von, Bis)ÞAusdruck Hinweis: Sie können diese Funktion über die Tastatur Ihres Computers eingeben, indem Sie sumSeq(...) eintippen. Wertet Ausdr1 für jeden Wert von Var zwischen Von und Bis aus und gibt die Summe der Ergebnisse zurück. Hinweis: Siehe auch Vorlage Summe, hier. |
|
|
G(Ausdr1, Var, Von, VonN1)Þ0 G(Ausdr1, Var, Von, Bis) ÞLG(Ausdr1, Var, Bis+1, VonN1) if Bis < VonN1
Die verwendeten Summenformeln wurden ausgehend von der folgenden Quelle entwickelt: Ronald L. Graham, Donald E. Knuth, Oren Patashnik: Concrete Mathematics: A Foundation for Computer Science. Reading, Massachusetts: Addison-Wesley 1994. |
|
|
Katalog > |
||||||||||
|
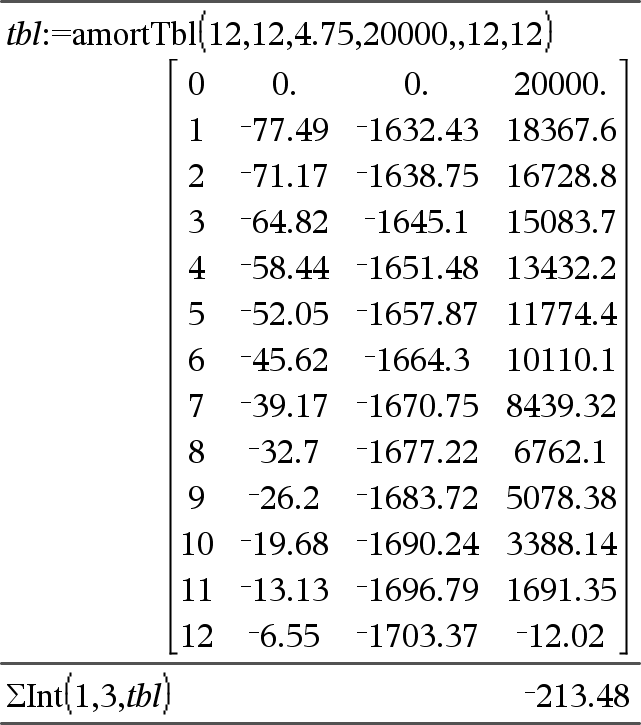
GInt(NPmt1, NPmt2, N, I, PV,[Pmt], [FV], [PpY], [CpY], [PmtAt], [WertRunden])ÞWert GInt(NPmt1,NPmt2,AmortTabelle)ÞWert Amortisationsfunktion, die die Summe der Zinsen innerhalb eines angegebenen Zahlungsbereichs berechnet. NPmt1 und NPmt2 definieren Anfang und Ende des Zahlungsbereichs. N, I, PV, Pmt, FV, PpY, CpY und PmtAt werden in der TVM-Argumentetabelle (hier) beschrieben.
WertRunden legt die Anzahl der Dezimalstellen für das Runden fest. Standard=2. GInt(NPmt1,NPmt2,AmortTable) berechnet die Summe der Zinsen auf der Grundlage der Amortisationstabelle AmortTabelle. Das Argument AmortTabelle muss eine Matrix in der unter amortTbl(), hier, beschriebenen Form sein. Hinweis: Siehe auch GPrn() auf dieser und Bal(), hier. |
|
|
Katalog > |
||||||||||
|
GPrn(NPmt1, NPmt2, N, I, PV, [Pmt], [FV], [PpY], [CpY], [PmtAt], [WertRunden])ÞWert GPrn(NPmt1,NPmt2,AmortTabelle)ÞWert Amortisationsfunktion, die die Summe der Tilgungszahlungen innerhalb eines angegebenen Zahlungsbereichs berechnet. NPmt1 und NPmt2 definieren Anfang und Ende des Zahlungsbereichs. N, I, PV, Pmt, FV, PpY, CpY und PmtAt werden in der TVM-Argumentetabelle (hier) beschrieben.
WertRunden legt die Anzahl der Dezimalstellen für das Runden fest. Standard=2. GPrn(NPmt1,NPmt2,AmortTabelle) berechnet die Summe der gezahlten Tilgungsbeträge auf der Grundlage der Amortisationstabelle AmortTabelle. Das Argument AmortTabelle muss eine Matrix in der unter amortTbl(), hier, beschriebenen Form sein. Hinweis: Siehe auch GInt() auf dieser und Bal(), hier. |
|
|
/k Tasten |
|
|
# varNameString Greift auf die Variable namens VarNameString zu. So können Sie innerhalb einer Funktion Variablen unter Verwendung von Strings erzeugen. |
Erzeugt oder greift auf die Variable xyz zu.
Gibt den Wert der Variable (r) zurück, dessen Name in Variable s1 gespeichert ist. |
|
i Taste |
|
|
MantisseEExponent Gibt eine Zahl in wissenschaftlicher Schreibweise ein. Die Zahl wird als Mantisse × 10Exponent interpretiert. Tipp: Wenn Sie eine Potenz von 10 eingeben möchten, ohne ein Dezimalwertergebnis zu verursachen, verwenden Sie 10^Ganzzahl. Hinweis: Sie können diesen Operator über die Tastatur Ihres Computers eingeben, indem Sie @E eintippen. Tippen Sie zum Beispiel 2.3@E4 ein, um 2.3E4 einzugeben. |
|
|
1 Taste |
|
|
Ausdr1gÞAusdruck Ausdr1gÞAusdruck Liste1gÞListe Matrix1gÞMatrix Diese Funktion gibt Ihnen die Möglichkeit, im Grad- oder Bogenmaß-Modus einen Winkel in Neugrad anzugeben. Im Winkelmodus Bogenmaß wird Ausdr1 mit p/200 multipliziert. Im Winkelmodus Grad wird Ausdr1 mit g/100 multipliziert. Im Neugrad-Modus wird Ausdr1 unverändert zurückgegeben. Hinweis: Sie können dieses Sonderzeichen über die Tastatur Ihres Computers eingeben, indem Sie @g eintippen. |
Im Grad-, Neugrad- oder Bogenmaß-Modus:
|
|
1 Taste |
|
|
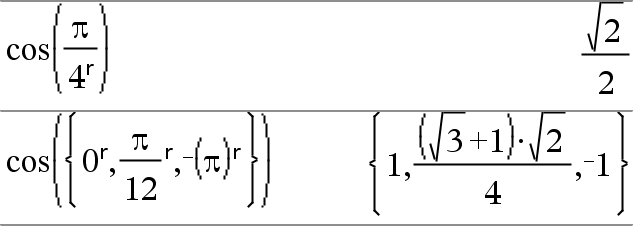
Liste1RÞListe Matrix1RÞMatrix Diese Funktion gibt Ihnen die Möglichkeit, im Grad- oder Neugrad-Modus einen Winkel im Bogenmaß anzugeben. Im Winkelmodus Grad wird das Argument mit 180/p multipliziert. Im Winkelmodus Bogenmaß wird das Argument unverändert zurückgegeben. Im Neugrad-Modus wird das Argument mit 200/p multipliziert. Tipp: Verwenden Sie R in einer Funktionsdefinition, wenn Sie bei Ausführung der Funktion das Bogenmaß frei von der Winkelmoduseinstellung erzwingen möchten. Hinweis: Sie können dieses Sonderzeichen über die Tastatur Ihres Computers eingeben, indem Sie @r eintippen. |
Im Winkelmodus Grad, Neugrad oder Bogenmaß:
|
|
1 Taste |
|
|
Liste1¡ÞListe Matrix1¡ÞMatrix Diese Funktion gibt Ihnen die Möglichkeit, im Neugrad- oder Bogenmaß-Modus einen Winkel in Grad anzugeben. Im Winkelmodus Bogenmaß wird das Argument mit p/180 multipliziert. Im Winkelmodus Grad wird das Argument unverändert zurückgegeben. Im Winkelmodus Neugrad wird das Argument mit 10/9 multipliziert. Hinweis: Sie können dieses Sonderzeichen über die Tastatur Ihres Computers eingeben, indem Sie @d eintippen. |
Im Winkelmodus Grad, Neugrad oder Bogenmaß:
Im Winkelmodus Bogenmaß: Hinweis: Erzwingen eines Näherungsergebnisses, Handheld: Drücken Sie / ·.
|
|
/k Tasten |
|||||||
|
dd¡mm'ss.ss''ÞAusdruck ddEine positive oder negative Zahl mmEine nicht negative Zahl ss.ssEine nicht negative Zahl Gibt dd+(mm/60)+(ss.ss/3600) zurück. Mit einer solchen Eingabe auf der 60er‑Basis können Sie:
Hinweis: Nach ss.ss werden zwei Apostrophe ('') gesetzt, kein Anführungszeichen ("). |
Im Grad-Modus:
|
|
/k Tasten |
|
|
[Radius,±q_Winkel]ÞVektor (Eingabe polar) [Radius,±q_Winkel,Z_Koordinate]ÞVektor (Eingabe zylindrisch) [Radius,±q_Winkel,±q_Winkel]ÞVektor (Eingabe sphärisch) Gibt Koordinaten als Vektor zurück, wobei die aktuelle Einstellung für Vektorformat gilt: kartesisch, zylindrisch oder sphärisch. Hinweis: Sie können dieses Sonderzeichen über die Tastatur Ihres Computers eingeben, indem Sie @< eintippen. |
Im Bogenmaß-Modus mit Vektorformat eingestellt auf: kartesisch
zylindrisch
sphärisch
|
|
(Größe ± Winkel)ÞkomplexerWert (Eingabe polar) Dient zur Eingabe eines komplexen Werts in polarer (r±q) Form. Der Winkel wird gemäß der aktuellen Winkelmoduseinstellung interpretiert. |
Im Winkelmodus Bogenmaß und Komplex-Formatmodus “kartesisch”:
Hinweis: Erzwingen eines Näherungsergebnisses, Handheld: Drücken Sie / ·.
|
|
º Taste
|
|
|
Variable ' Variable '' Gibt in einer Differentialgleichung einen Ableitungsstrich ein. Ein Ableitungsstrich kennzeichnet eine Differentialgleichung erster Ordnung, zwei Ableitungsstriche kennzeichnen eine Differentialgleichung zweiter Ordnung usw. |
|
|
Siehe “Leere (ungültige) Elemente” , hier. |
|
|
|
|
|
/_ Tasten |
|
|
Ausdr_Einheit Kennzeichnet die Einheiten für einen Ausdr. Alle Einheitennamen müssen mit einem Unterstrich beginnen. Sie können entweder vordefinierte Einheiten verwenden oder Ihre eigenen erstellen. Eine Liste vordefinierter Einheiten finden Sie im Katalog auf der Registerkarte Einheiten-Konversion (Unit Conversions). Sie können Einheitennamen aus dem Katalog auswählen oder sie direkt eingeben. |
Hinweis: Das Umrechnungssymbol 4 können Sie im Katalog finden. Klicken Sie auf |
|
Variable_ Besitzt Variable keinen Wert, so wird sie behandelt, als würde sie eine komplexe Zahl darstellen. Die Variable wird ohne das Zeichen _ standardmäßig als reell behandelt. Besitzt Variable einen Wert, so wird das Zeichen _ ignoriert und Variable behält ihren ursprünglichen Datentyp bei. Hinweis: Eine komplexe Zahl kann ohne Unterstrich _ in Variablen gespeichert werden. Bei Berechnungen wie cSolve() und cZeros() empfiehlt sich allerdings die Verwendung von _, um beste Ergebnisse zu erzielen. |
z sei undefiniert:
|
|
/k Tasten |
|||||||
|
Ausdr_Einheit1 4 _Einheit2ÞAusdr_Einheit2 Konvertiert einen Ausdruck von einer Einheit in eine andere. Der Unterstrich _ kennzeichnet die Einheiten. Diese Einheiten müssen sich in derselben Kategorie befinden, z.B. Länge oder Fläche Eine Liste vordefinierter Einheiten finden Sie im Katalog auf der Registerkarte Einheiten-Konversion (Unit Conversions):
Sie können die Einheitennamen auch manuell eingeben. Um bei der Eingabe von Einheitennamen auf dem Handheld “_” einzugeben, drücken Sie /_. Hinweis: Verwenden Sie zum Konvertieren von Temperatureinheiten tmpCnv() und @tmpCnv(). Der Konvertierungsoperator 4 ist nicht für Temperatureinheiten anwendbar. |
|
|
Katalog > |
|
|
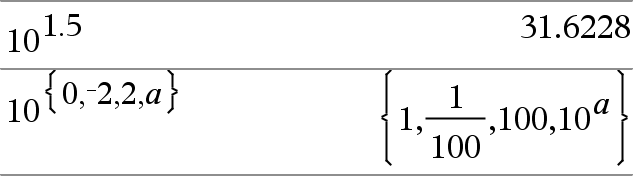
10^(Ausdr1)ÞAusdruck 10^(Liste1)ÞListe Gibt 10 hoch Argument zurück. Bei einer Liste wird 10 hoch jedem Element von Liste1 zurückgegeben. |
|
|
10^(Quadratmatrix1)ÞQuadratmatrix Ergibt 10 hoch Quadratmatrix1. Dies ist nicht gleichbedeutend mit der Berechnung von 10 hoch jedem Element. Näheres zur Berechnungsmethode finden Sie im Abschnitt cos(). Quadratmatrix1 muss diagonalisierbar sein. Das Ergebnis enthält immer Fließkommazahlen. |
|
|
Katalog > |
|
|
Liste1 ^/ÞListe Gibt den Kehrwert des Arguments zurück. Bei einer Liste wird für jedes Element von Liste1 der Kehrwert zurückgegeben. |
|
|
Quadratmatrix1 ^/ÞQuadratmatrix Gibt die Inverse von Qudratmatrix1 zurück. Quadratmatrix1 muss eine nicht-singuläre quadratische Matrix sein. |
|
|
/k Tasten |
||||||||||
|
Ausdr | BoolescherAusdr1 [ Ausdr | BoolescherAusdr1 [ Das womit-Symbol („|“) dient als binärer Operator. Der Operand links von | ist ein Ausdruck. Der Operand rechts von | gibt eine oder mehrere Relationen an, die auf die Vereinfachung des Ausdrucks einwirken sollen. Bei Angabe mehrerer Relationen nach dem | sind diese jeweils mit logischen „ Der womit-Operator erfüllt drei Grundaufgaben:
|
|
|||||||||
|
Ersetzungen werden in Form einer Gleichung angegeben, wie etwa x=3 oder y=sin(x). Am wirksamsten ist eine Ersetzung, wenn die linke eine einfache Variable ist. Ausdr | Variable = Wert bewirkt, dass jedes Mal, wenn Variable in Ausdr vorkommt, Wert ersetzt wird. |
|
|||||||||
|
Intervallbeschränkungen werden in Form einer oder mehrerer mit logischen „ |
|
|||||||||
|
Ausschließungen verwenden den relationalen Operator „ungleich“ (/= oder ƒ), um einen bestimmten Wert bei der Operation auszuschließen. |
|
|
/h Taste |
|
|
Liste & Var Matrix & Var Expr & Funktion(Param1,...) List & Funktion(Param1,...) Matrix & Funktion(Param1,...) Wenn Variable Var noch nicht existiert, wird Var erzeugt und auf Ausdr, Liste oder Matrix initialisiert. Wenn Var existiert und nicht gesperrt oder geschützt ist, wird der Variableninhalt durch Ausdr, Liste oder Matrix ersetzt. Tipp: Wenn Sie symbolische Rechnungen mit undefinierten Variablen vornehmen möchten, sollten Sie vermeiden, Werte in Variablen mit häufig benutzten Einzeichennamen abzuspeichern (etwa den Variablen a, b, c, x, y, z usw.). Hinweis: Sie können diesen Operator über die Tastatur Ihres Computers eingeben, indem Sie das Tastenkürzel =: eintippen. Geben Sie zum Beispiel pi/4 =: myvar ein. |
|
|
/t Tasten |
|
|
Var := Liste Var := Matrix Function(Param1,...) := Ausdr Function(Param1,...) := Liste Function(Param1,...) := Matrix Wenn Variable Var noch nicht existiert, wird Var erzeugt und auf Ausdr, Liste oder Matrix initialisiert. Wenn Var existiert und nicht gesperrt oder geschützt ist, wird der Variableninhalt durch Ausdr, Liste bzw. Matrix ersetzt.
|
|
|
/k Tasten |
|
|
© [Text] © verarbeitet Text als Kommentarzeile und ermöglicht so die Eingabe von Anmerkungen zu von Ihnen erstellten Funktionen und Programmen. © kann an den Zeilenanfang oder an eine beliebige Stelle der Zeile gesetzt werden. Alles, was rechts von © bis zum Zeilenende steht, gilt als Kommentar. Hinweis zum Eingeben des Beispiels: Anweisungen für die Eingabe von mehrzeiligen Programm- und Funktionsdefinitionen finden Sie im Abschnitt „Calculator“ des Produkthandbuchs. |
|
|
0B Tasten, 0H Tasten |
|
|
0b binäre_Zahl 0h hexadezimale_Zahl Kennzeichnet eine Dual- bzw. Hexadezimalzahl. Zur Eingabe einer Dual- oder Hexadezimalzahl muss unabhängig vom jeweiligen Basis-Modus das Präfix 0b bzw. 0h verwendet werden. Eine Zahl ohne Präfix wird als dezimal behandelt (Basis 10). Die Ergebnisse werden im jeweiligen Basis-Modus angezeigt. |
Im Dec-Modus:
Im Bin-Modus:
Im Hex-Modus:
|








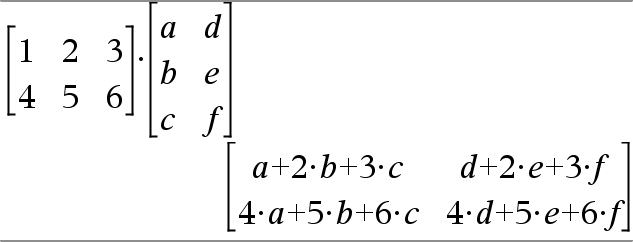












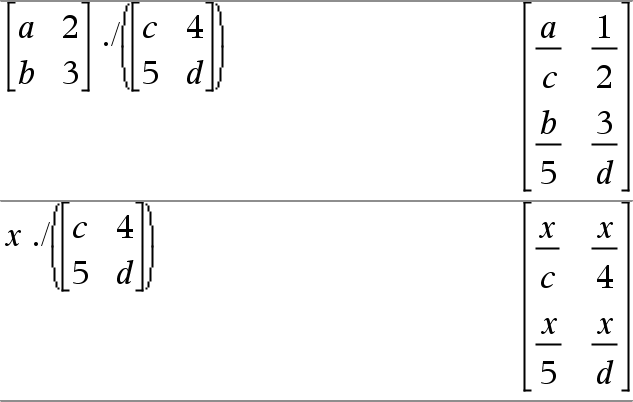

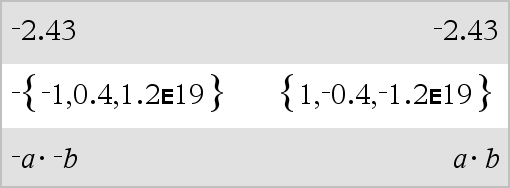
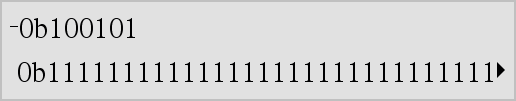
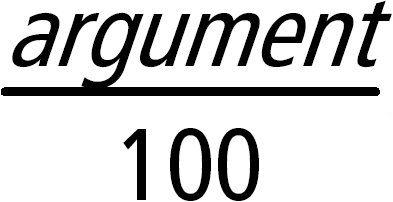
 aus.
aus.


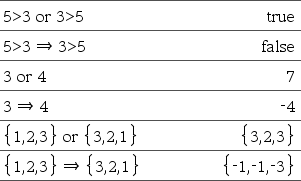
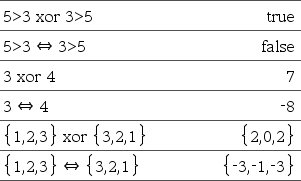



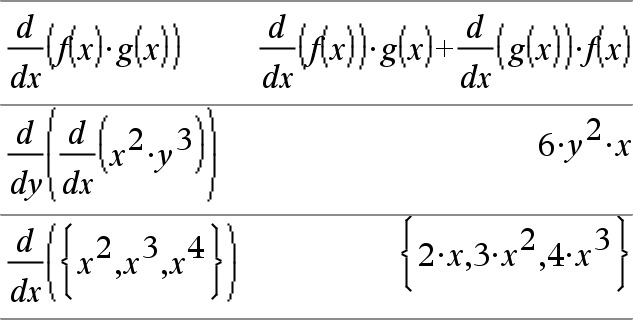


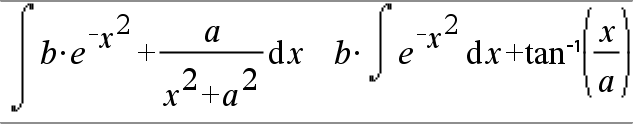

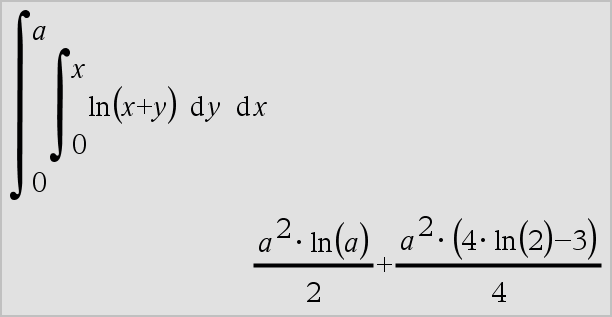

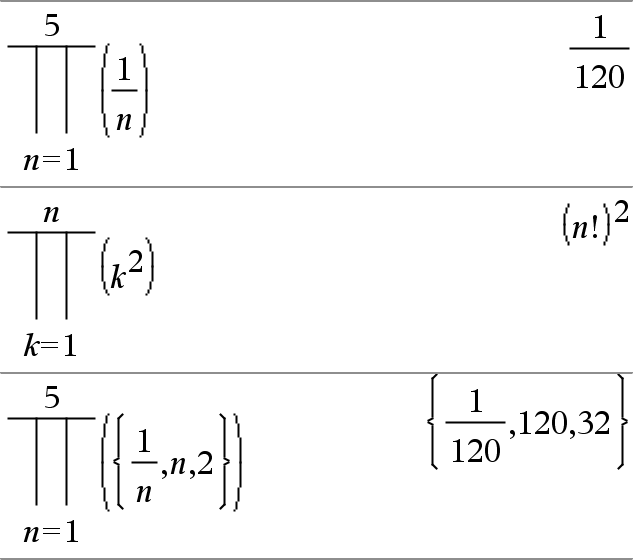

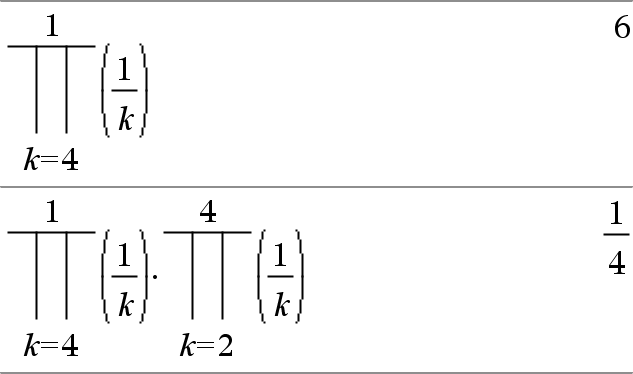
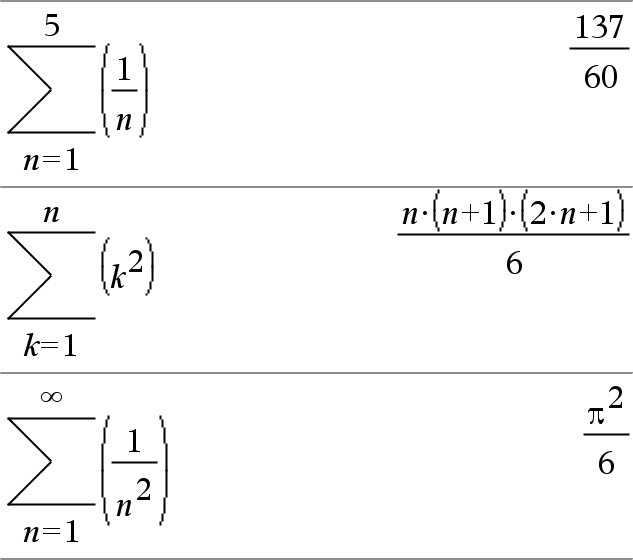

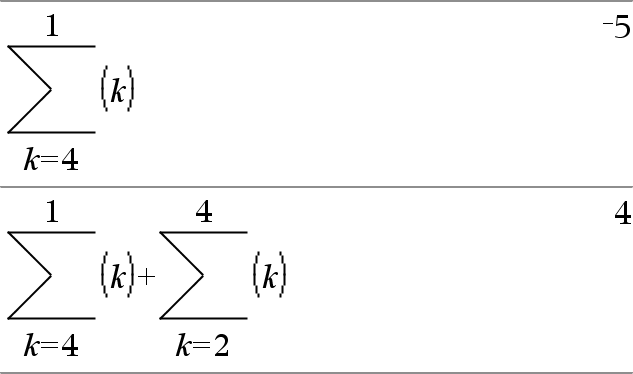
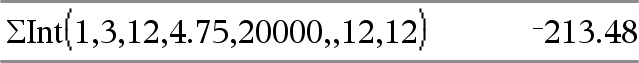
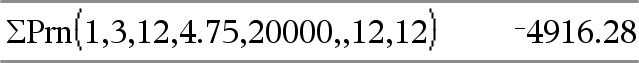






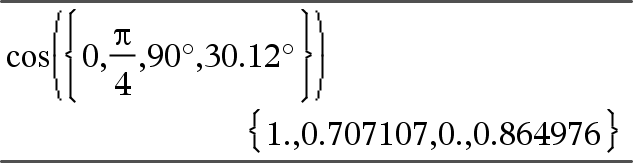

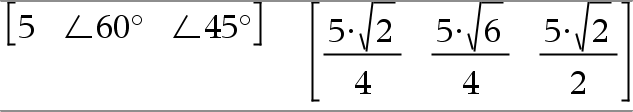
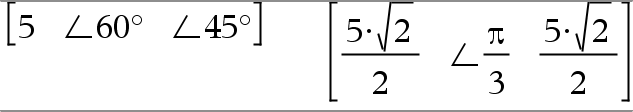

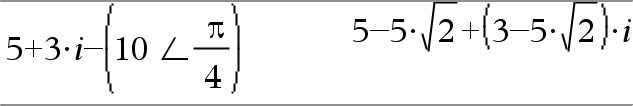
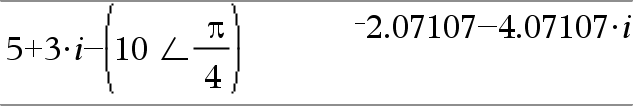
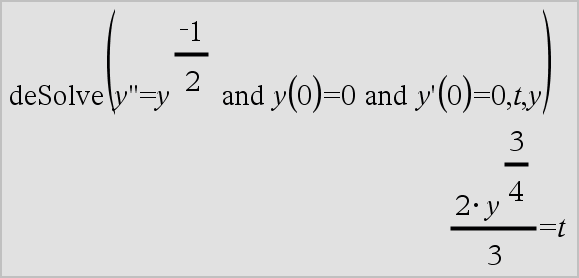

 und dann auf
und dann auf