In Lesson 22.2 you found Maclaurin series that approximate functions near x = 0. This lesson investigates how to find a series that approximates a function near x = a, where a is any real number.

Defining a Taylor Series

Given a function f that has all its higher order derivatives, the series

where

is called the Taylor series for f centered at a. The Taylor series is a power series that approximates the function f near x = a.

The partial sum

is called the nth-order Taylor polynomial for f centered at a.

Every Maclaurin series, including those studied in Lesson 22.2, is a Taylor series centered at zero.

Finding Taylor Polynomials

The TI-89 taylor( command can be used to find partial sums of Taylor series.

Taylor Command The syntax for the taylor( command is taylor(expression, var, order, point) where expression, var, and order are defined as before and point is the value of "a" around which the series is centered. The parameter point is optional and if omitted the series generated will be a Maclaurin series, which is centered at 0.

Find the second-order Taylor polynomial centered at 1 for the function f(x) = e^x.

• Enter taylor(e^x, x, 2, 1)

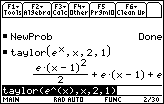
Near

The series above is similar to the Maclaurin series for y = e^x found in Lesson 22.2. However, the terms in this series have powers of (x - 1) rather than powers of x and the coefficients contain the values of the derivatives evaluated at x = 1. The coefficient of the term (x - 1)^k is

More Taylor Polynomials

The polynomial you found in Lesson 22.2, , was tangent to y = e^x at x = 0 and has the same concavity as y = e^x at that point. The polynomial , which is centered at
x = 1, is tangent to y = e^x at x = 1 and has the same concavity as y = e^x at that point.

22.3.1 Find the fifth-degree Taylor polynomial centered at 1 for y = ln x and interpret the result. Click here for the answer.

22.3.2 Find the fourth-degree Taylor polynomial centered at 1 for . Click here for the answer.

22.3.3 Describe the relationship between the two polynomials found in 22.3.1 and 22.3.2. Click here for the answer.

22.3.4 Predict the relationship between the fifth-degree Maclaurin polynomial for y = sin x and the fourth-degree Maclaurin polynomial for y = cos x. Click here for the answer.

Verify your prediction of the relationship between the Maclaurin polynomials for
y = sin x and for y = cos x with the commands show below.

• Execute taylor(sin(x), x, 5)

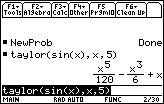
• Enter the derivative command d( on the Edit Line
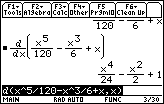
• Paste the last result from the History Area to the Edit Line
• Execute d(x^5/120 – x^3/6 + x, x)

Find the fourth-degree Maclaurin polynomial for y = cos x.

• Execute taylor(cos(x), x, 4)

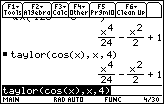
The results are the same as predicted.