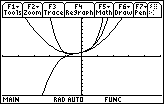
The graphs appear to coincide approximately on the interval (-1/2, 1/2).
y = 1 + x + x2 + ... + x10 =
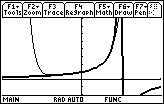
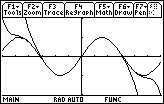
The graphs appear to converge to y = sin x around x = 0.
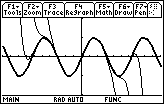

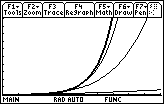
As more terms are added, the interval where the partial sums are approximately the same as ex widens. The interval of convergence for the infinite power series is (–
![]() ,
,
![]() )
)
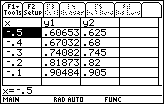
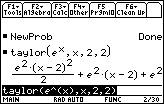
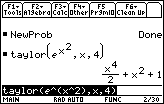
The quadratic polynomial is 0.01847 greater than the actual value of y = ex when x = -0.5 and 0.02372 less than the actual value of y = ex when x = 0.5.
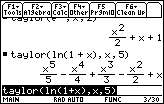
![]()

Near
![]() .
.
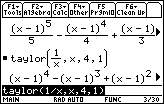
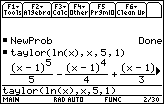
Near
![]() .
.
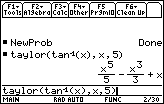
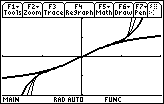
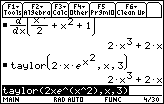
The interval of convergence appears to be (-1,1).

©Copyright 2007 All rights reserved. | Trademarks | Privacy Policy | Link Policy