In this lesson you will explore an application that is modeled by using exponential decay. The model used is similar to the one explored in Lesson 19.1.

Modeling Cooling Temperatures

A hot liquid left in a cup cools to the temperature of the surroundings. Newton's Law of Cooling describes the liquid's temperature and it says that:
    the temperature cools at a rate proportional to the difference between the liquid's temperature and the temperature of its surroundings.

Let the following variables represent the relevant quantities.

tL = Temperature of the liquid

tS = Temperature of the surroundings

t = Time

tL₀ = Temperature of the liquid at t = 0

By Newton's Law of Cooling,

tL' = –k(tL – tS)

where k is the constant of proportionality and tL' represents the rate at which the temperature of the liquid is changing. The negative sign in front of k indicates that the temperature of the liquid is decreasing.

Finding the Temperature Equation

An equation for temperature can be found by solving the differential equation with the initial condition that the temperature of the liquid at t = 0 is tL₀.

Solve the initial-value problem tL' = –k(tL – tS) and tL(0) = tL₀

• Perform NewProb
• deSolve(tL' = -k*(tL - tS) and tL(0) = tLo, t ,tL)

Insert the multiplication symbol between -k and (tL-tS) and use the letter "o" in tLo.

Upper and Lower Case Letters The TI-89 converts all upper-case letters to lower case in displayed results.

The equation that gives the temperature of the liquid at time t is

tL = (tL₀ – tS)e^–kt + tS

Finding a Specific Solution

A specific solution to a cooling problem whose solution is given by tL = (tL₀ – tS)e^–kt + tS can be found by using the following procedure.

1. Find the value of k by using values of the initial temperature, the temperature of the surroundings and particular values of the liquid's temperature at a given time.
2. Using the value of k found, the equation that gives the liquid's temperature can be used to find temperatures at other times.

Suppose a cup of water was heated to a temperature of 65°C and placed in a refrigerator that had a temperature of 5°C. The water cooled to a temperature of 11°C in 30 minutes. Find the temperature of the water after 60 minutes.

The solution is found by using the values below.

The initial temperature of the water is 65: tLo = 65.

The surrounding temperature is 5: tS = 5.

Specific values used to find k are tL = 11 when t = 30.

The question asks you to find the temperature of the water after 60 minutes.

Store the given values in tLo and tS with the following commands:

Deleting a Variable's Value The variables tLo and tS have been defined with the values 65 and 5. NewProb will not delete these variables because their names are longer than one letter. If you would like to delete these variables at a later time, you will need to use the DelVar command, which is found in the Catalog. DelVar tLo, tS Alternatively, you can press [VAR-LINK] and [F1: MANAGE] to delete the variable.

Solve for k by entering the command "solve(" on the Edit Line, pasting the equation for TL from the History Area and completing the command by inserting the particular information tL = 11 and t = 30.

• solve(tl = (tlo - ts)*e^(-k*t) + ts, k) | tl=11 and t=30

To determine the temperature of the liquid after 60 minutes, evaluate the expression

tL = (tLo – tS)e ^ (–k * t) + tS with and t = 60:

• Paste the equation for tL to the Edit Line from the History Area
• Press
• Paste the expression 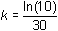to the end of the current expression in the Edit Line
• Enter "and t = 60" to complete the command

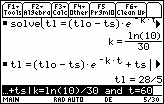
The water will be about 28/5, or 5.6°C, in 60 minutes.

19.2.1 A cup of water was heated to a temperature of 70°C and placed in a refrigerator that had a temperature of 8°C. The water cooled to a temperature of 14°C in 30 minutes. Find the temperature of the water after 60 minutes.
Click here for the answer.