In this lesson you will explore the first of three applications where the change in an amount is directly proportional to the amount present. The first type of application is continuously compounded interest, which is represented by an exponential growth model.
Modeling Continuous Compound Interest
When interest on an account is compounded continuously, the account grows at a rate that is directly proportional to the size of the account. In other words the larger the account the faster it grows. This can be described by the differential equation
A' = rA
where A is the size of the account after t years and r is the annual interest rate in decimal form. A', the first derivative of A with respect to time, represents the rate at which A is changing.
Exploring Continuous Compound Interest
Suppose an account has an annual interest rate of 6.5% and it is compounded continuously. The equation for the amount in the account can be found by solving the the initial value problem
A' = 0.065A and A(0) = p
The first equation indicates that the rate of change of the amount in the account, A', is directly proportional to the amount in the account, A. The constant of proportionality is 0.065. The second equation indicates that the initial amount at time 0 is p.
- Perform NewProb
- Enter deSolve(a' = 0.065a and a(0)=p,t,a).
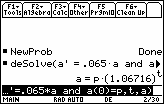
The amount in the account after t years is approximately a = p(1.06716)t, where p is the original amount in the account.
|
|||
|
|
|||
Finding Doubling Time
Find the time required to double the original amount by solving 2p = p · (1.06716)t for t.
- Solve(2p=p·(1.06716)^t,t)
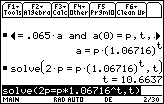
The account will double in about 10.7 years.
19.1.1 Find the doubling time for an investment that is compounded continuously at 8%.
Click here for the answer.
Finding Future Amounts
Suppose $1000 is deposited into an account that pays interest compounded continuously at an annual rate of 7%. Determine how much the account will be worth in 30 years.
- Perform NewProb
- Solve the initial value problem a' = 0.07a and a(0) = 1000
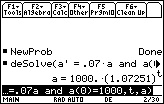
- Evaluate a = 1000(1.07251)t with t = 30
Paste the last expression in the History Area to the Edit Line and then append "| t=30".

The investment will grow to $8,166.17 in 30 years.
19.1.2 How much will in initial investment of $5,000 be worth in 35 years if it earns interest compounded continuously at an annual rate of 8.5%?
Click here for the answer.
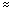 1.06716.
1.06716.