This lesson introduces the Arc Length Theorem and uses it's formula to compute the length of an arc of a curve. The lesson also explores using the TI-89's arc length feature, which is found in the Graph menu, and the arc length function, which is a built-in TI-89 function.

The length of an arc of a section of a curve can be found by using an integral, as shown in the following theorem.

Arc Length Theorem

If a curve y = f(x) has a continuous derivative on the interval [a, b], its arc length is given by

Using the Theorem to Find Arc Length

The theorem often gives integrals that are difficult or impossible to evaluate by hand. The TI-89 can be very helpful in evaluating or approximating these integrals.

Find the length of the curve y = x^2/3 on the interval [1, 2].

• Define f(x)=x^(2/3)
• Evaluate the integral by entering

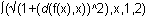
Keep the entry in the History Area for use later in this lesson.

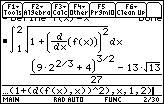
The decimal approximation of the exact result is 1.16024 units.

Using the Arc Length Feature

There is an arc length feature in the Graph Math menu.

• Graph y = x^2/3 in a [0, 3] x [0, 3] window

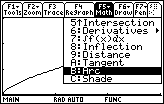
• Open the Math menu by pressing
• Scroll down the menu and highlight "B:Arc"

• Select the Arc feature by pressing

The calculator should prompt you for the first point, which is the left bound of the arc.

• Enter 1

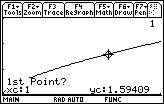
After pressing to save the left endpoint of the interval, the cursor will move to the left bound and you should see a prompt for the second point, which is the right bound.

• Enter 2

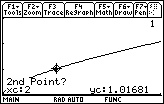
After pressing to save the right endpoint of the interval, you will see the graph with markers for the bounds. The approximate arc length is displayed at the bottom of the screen.

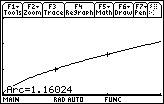
The answer matches the approximation found using the theorem.

17.3.1 Find the exact length of the curve y = x² on the interval [-1, 2] and find a decimal approximation.

Pasting from the History Area Don't clear the History Area before doing the problem. After defining f(x)=x^2 you can scroll in the History Area and paste the previous definite integral for arc length to the Edit Line. Edit the limits of integration and press to see the new arc length.

Click here for the answer.

17.3.2 Use the Arc feature of the Graph Math menu to approximate the arc length of y = x² on the interval [-1, 2]. Compare the result with the answer found in Question 17.3.1.
Click here for the answer.

Using the arcLen Function

The arcLen function, which is found in the catalog or by pressing , can also be used to find arc lengths.

arcLen Syntax The syntax for the arcLen function is arcLen(expression,var,start,end)

• Execute NewProb
• Define f(x)=x^(2/3)
• Display the catalog by pressing and press ([A])
• Scroll down until the cursor points to arcLen(

• Paste "arcLen(" to the Edit Line by pressing
• Enter arcLen(f(x),x,1,2)

This is the same answer obtained using the theorem at the beginning of this lesson.