In previous modules you used the definite integral to find the area bounded by a function and the x-axis. In each case the graph of the function was above the x-axis. In this lesson you will see what happens when the function dips below the x-axis. You will also investigate the concept of the definite integral as a net area function.

All the curves explored in Module 16 were above the x-axis and the net area functions were always positive and increasing. The following investigates a definite integral when part of the curve is below the x-axis.

• Graph y = sin x in a [0, 2 ] x [-1, 1] window

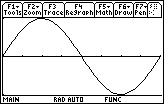
• Evaluate the integral 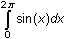by using the integral key

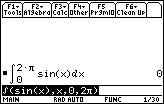
How can the result be zero? The area bounded by y = sin x and the x-axis certainly is not zero. To help answer this question, break the interval of integration into two subintervals that represent the areas above and below the x-axis: (0, ) and ( , 2 ).

• Evaluate 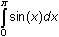and

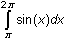
Finding Positive and Negative Integrals

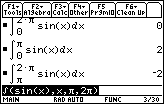
Review the graph of y = sin x and the values of the definite integrals and .

Toggle between Screens You can toggle between the Home screen and the Graph screen by pressing .

 

The graph from 0 to is above the x-axis and the corresponding definite integral is positive.

The graph from to 2 is below the x-axis and the corresponding definite integral is negative.

Finding Net Area

The definite integral represents the value of the net area, or the area above the x-axis minus the area below the x-axis. The net area between the curve y = sin x and the x-axis is zero because it is the sum of 2, the area above the axis, and –2, the negative of the area below the axis.

17.1.1 Use the definite integral feature in the F5:Math menu of the Graph screen to approximate the values of

Click here for the answer.

Visualizing

You may obtain the general shape of a corresponding net area function on the interval [0, 2 ] by examining the graph of y = sin x.

• Refresh the graph of y = sin x by pressing

The following characteristics of the net area function can be determined from the graph of the curve y = sin x. Look at the graph while reading the tables below.

Interval	Curve Function	Area Function
and	increasing	concave upward
	decreasing	concave downward

Using the fact that
the value of the curve function is the derivative of the net area function,
the x-values of maximums, minimums and points of inflection can be identified by examining how the curve is changing.

x-value	Curve Function is Changing	Area Function
x =	from positive to negative	maximum
	from increasing to decreasing	point of inflection
	from decreasing to increasing	point of inflection

Other characteristics of the net area function include:

1. The net area when x = 0 is 0.
2. The net area on the interval [0, ] is 2 and the net area function begins to decrease at that point, so the maximum of the net area function is 2 when x = .
3. The net area on the interval [0, 2 ] is 0, so the net area function is 0 when x = 2 .

With these characteristics you can draw a graph of the net area function , as shown below together with the graph of the curve.

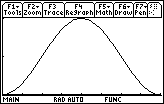
y = sin x

Visualizing the general shape of the integral function is often very helpful.

Extending the Procedure to Other Curves

17.1.2 Graph the curve and find the net area bounded by y = x³ – 3x² – x + 3 and the x-axis on the interval [0, 4].

Click here for the answer.

Visualizing

The characteristics of the net area function can be found by examining the graph of the curve function. The graph of the curve is shown below in a [0, 4] x [ -5, 15] window with a list of the net area function's characteristics.

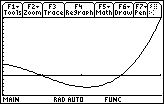
y = x3 – 3x2 – x + 3

When x = 0 the net area function is 0. The net area function is concave downward on (0, 2.1547) because the curve is decreasing there. The net area function is concave upward on (2.1547, 4) because the curve is increasing there. Because the curve changes from positive to negative at x = 1, the net area function has a local maximum there. Because the curve changes from negative to positive at x = 3, the net area function has a local minimum there. The area from 0 to 1 appears to be the same as the area from 1 to 2, so the net area function is 0 when x = 2. This can be confirmed by evaluating the integral From 2 to somewhere beyond 3 the net area function is negative because more of the area is below the x-axis to that point. Somewhere beyond 3 the net area function becomes positive because more area is above the x-axis than below it.

The graphs of the curve function and the net area function are shown below for comparison.

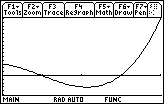
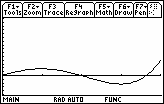
y = x3 – 3x2 – x + 3

17.1.3 Approximate the graph of a net area function that corresponds to the following curve from 0 to 4.

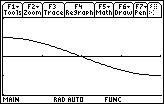
Click here for the answer.