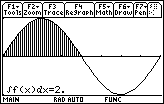


The value of the integral over [0,
![]() ] where the area is above the x-axis, is 2. The value of the integral over [
] where the area is above the x-axis, is 2. The value of the integral over [
![]() ,2
,2
![]() ] where the area is below the x-axis, is -2. Therefore the net area over
[0, 2
] where the area is below the x-axis, is -2. Therefore the net area over
[0, 2
![]() ] is 0.
] is 0.
The net area is
![]() square units, which is the sum of the two areas that lie above the x-axis minus the area that lies below the x-axis.
square units, which is the sum of the two areas that lie above the x-axis minus the area that lies below the x-axis.
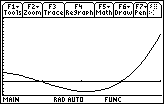
- The curve is decreasing on (0, 4), so the area function is concave downward on the interval.
- The curve is positive when x < 2 and negative when x > 2, so the area function has a maximum at x = 2.
- The curve appears to have equal areas above and below the x-axis on the interval, so the area function is 0 when x = 4.
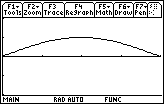
A Net Area Function
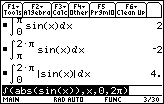
The total area between f(x) = sin x and the x-axis between x = 0 and x = 2
![]() is 4 square units.
is 4 square units.
The TI-89 is not able to integrate
![]() , as indicated by the result being the same as the command.
, as indicated by the result being the same as the command.
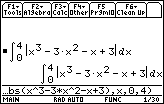
However, the graph of y = x3 – 3x2 – x + 3 on the interval [0, 4] has two regions above the x-axis and one below.
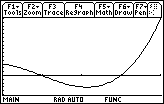
The window is [0, 4] x [-5, 15].
After finding the zeros of the curve (x = 1 and x = 3), integrate the curve over the separate intervals
![]()
![]()
![]()
The total area is
![]() square units.
square units.
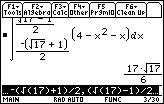
The area between the curves is
![]() , or approximately 11.6821 square units.
, or approximately 11.6821 square units.
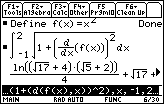
The exact answer is
![]() , which is approximately 6.12573 units.
, which is approximately 6.12573 units.
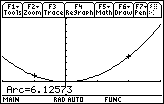
The result is the same as the decimal approximation found in Question 17.3.1.
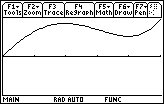
One possible net area function is shown below.
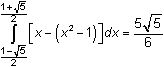
©Copyright 2007 All rights reserved. | Trademarks | Privacy Policy | Link Policy