- Use the Derivative feature of the Graph Math menu to find f '(1.5).
-
Use the Tangent feature of the Graph Math menu to find the equation of the tangent line to
y = f(x) at x = 1.5. -
Refresh the graph screen by pressing
 and use the Inflection feature of the Graph Math menu to find the inflection point of y = f(x).
and use the Inflection feature of the Graph Math menu to find the inflection point of y = f(x).
- Find the intervals where the graph of f is concave upward and where it is concave downward.
- Display the graphs of the function f and its derivative and use the graph of the derivative to determine where the turning points of f occur.
- Use the graph of the derivative of f to determine where f is increasing and where f is decreasing.
-
Use the Derivative key to find the second derivative of
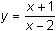
Define f(x) = –x3 + 2x2 + 4x –3 and graph it in a [-7.9, 7.9] x [-6, 6] window.
Click here to check your answers.