In Module 8 we saw that the value of the derivative of f at x is given by the slope of the line tangent to the graph of f at x. In this lesson you will explore what the first derivative says about the graph of the original function by using the Derivative and Tangent features of the calculator.

If f is a function, then its first derivative is denoted by f ' , which is read "f prime," and the value of the first derivative at x = a is f '(a). The calculator denotes the first derivative of f as , which is an alternate notation. If y = f(x), other notations include , and dy/dx.

Using the Derivative Feature on the Graph Screen

Follow the procedure given below to graph a function and use the Derivative feature of the Graph screen's Math menu to compute its derivative.

• Graph y = x³ – 2x² – 5x + 6 in a [-5, 5] x [-10, 10] window

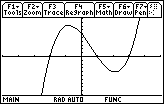
Find the value of the derivative at x = -2 with the Derivative feature in the F5:Math menu.

• Display the Math menu by pressing
• Highlight 6:Derivatives by using the cursor movement keys
• Open the Derivative submenu by pressing

• Select dy/dx by pressing

You should see the graph and a prompt for the x-coordinate at which the derivative is to be evaluated.

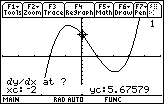
• Enter -2 as the x-coordinate by pressing

• Set the value of the x-coordinate by pressing

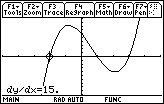
The value of the derivative of f(x) = x³ – 2x² – 5x + 6 at x = -2 is 15.

Using the Tangent Feature

You can use the Tangent feature of the Graph Math menu to see the graph of a tangent line at a specific point along with the equation for that tangent line.

• Open the Math menu and select A:Tangent

After you make the selection, you should see the graph of the function and a prompt for the x-coordinate of the point of tangency.

• Enter -2. Then press

 

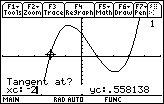
The TI-89 displays the graph of the tangent line and its equation is shown at the bottom of the screen. The equation of the tangent line in the example above is y = 15x + 30.

9.1.1 How does the equation of the tangent line display the value of the derivative at x = -2? Click here for the answer.

9.1.2 The table below contains points on the graph of the function f(x) = x³ – 2x² – 5x + 6. Use the Derivative feature to find the derivative at each point shown and record the values.

x	–2	–1	0	1	2	3
f(x)	0	8	6	0	–4	0
f ' (x)

Click here for the answer.

9.1.3 What do you notice about the function values on the intervals where the derivative is positive compared with the function values on the intervals where the derivative is negative?
Click here for answer.

• Redraw the graph and clear the tangent line by pressing

Derivative and Tangent Features on the Graph Screen The Derivative and the Tangent features on the graph screen give approximate results. The Derivative command on the Home Screen gives exact results.

Finding Turning Points from the Derivative

Every

A turning point of the graph of a function is a point where the function changes from increasing to decreasing or changes from decreasing to increasing.

turning point of a function has a derivative of zero at that point if it is differentiable at that point. Graphing the derivative with the function can illustrate how to find these turning points.

• Set y2=d(y1(x),x)

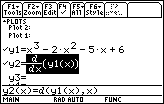
• Display the graph of the function and its derivative by pressing

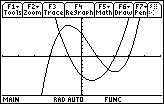
The function is increasing exactly where the derivative is positive, and decreasing exactly where the derivative is negative. On the graph of the derivative find the x-value of the zero to the left of the origin.

• Select the Zero feature in the F5:Math menu
• Select the graph of the derivative by pressing
  A small 2 should appear in the upper right-hand corner to indicate that the graph defined in y2 is selected.
• Set the lower bound by moving the cursor to the left of the desired zero and pressing
• Set the upper bound by moving the cursor to the right of the desired zero and pressing

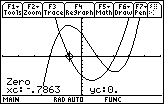
One of the zeros of the derivative is approximately x = -0.7863.

9.1.4 Use the Zero feature of the F5:Math menu to find the other zero of the derivative. Click here for the answer.

Summarizing the Relationship between f and f '

The following characteristics of the function f(x) = x³ – 2x² – 5x + 6 can be determined from the graph of its first derivative.

The derivative is zero at x = -0.7863 and at x = 2.11963, which are the x-values of the turning points.

The function is increasing on the intervals (- , -0.7863) and (2.11963, ) because its first derivative is positive there.

The function is decreasing on the interval (-0.7863, 2.11963) because its first derivative is negative there.