|
Module 9 - Answers
|
|
|
|
Lesson 1
|
|
|
|
Answer 1
|
|
|
|
9.1.1
The slope of the tangent line is the coefficient of x in the tangent's equation, y = 15x + 30. Because the slope of the tangent line at a point is also the value of the derivative at that point, the derivative at x = –2 is 15, the coefficient of x in the equation for the tangent.
|
|
|

|

|
|
Answer 2
|
|
|
|
9.1.2
|
x
|
–2
|
–1
|
0
|
1
|
2
|
3
|
|
f(x)
|
0
|
8
|
6
|
0
|
–4
|
0
|
|
f' (x)
|
15
|
2
|
–5
|
–6
|
–1
|
10
|
|
|
|

|

|
|
Answer 3
|
|
|
|
9.1.3
The function is increasing where the derivative is positive and decreasing where the derivative is negative.
|
|
|

|

|
|
Answer 4
|
|
|
|
9.1.4
The other zero is approximately x = 2.11963.
|
|
|

|

|
|
Lesson 2
|
|
|
|
Answer 1
|
|
|
|
9.2.1
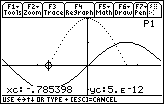
The slopes of the tangent lines increase on the interval
 and decrease on the interval
and decrease on the interval
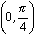 .
.
|
|
|

|

|
|
Answer 2
|
|
|
|
9.2.2
If the derivative (f') is increasing, then its derivative (f") must be positive. If the derivative (f') is decreasing, then its derivative (f") must be negative. When the second derivative is positive the original function is concave up. When the second derivative is negative the original function is concave down. The graph of y = sin2x appears to change from concave upward to concave downward at x = 0.
|
|
|

|

|
|
Answer 3
|
|
|
|
9.2.3
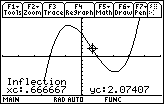
The coordinates of the inflection point are approximately (0.67, 2.07)
|
|
|

|

|
|
Answer 4
|
|
|
|
9.2.4
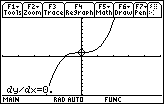
The first derivative is zero at x = 0. This is not a turning point but rather an inflection point. Both the first and second derivatives are zero at this point and the concavity changes from concave downward to concave upward there.
|
|
|

|

|
|
Self Test
|
|
|
|
Answer 1
|
|
|
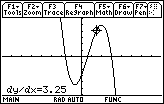
|
|
|
|
Answer 2
|
|
|

|
|
|
|
Answer 3
|
|
|
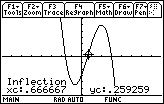
|
|
|
|
Answer 4
|
|
|
The graph of f is concave upward on the interval (-
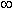 , 0.6667) and concave downward on the interval (0.6667,
, 0.6667) and concave downward on the interval (0.6667,
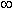 )
)
|
|
|
|
Answer 5
|
|
|
Turning points of f occur at x = –0.667 and x = 2.


|
|
|
|
Answer 6
|
|
|
f is increasing on the interval (-0.667, 2) and decreasing on the intervals (-
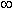 , -0.667) and (2,
, -0.667) and (2,
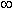 ).
).
|
|
|
|
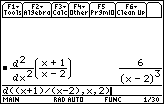
Answer 7
|
|
|
|
|
|

|
©Copyright
2007 All rights reserved. |
Trademarks
|
Privacy Policy
|
Link Policy
|

![]() and decrease on the interval
and decrease on the interval
![]() .
.







