In this lesson you will use a computer algebra system to create a mathematical laboratory where experiments are conducted, patterns are discovered, and conjectures are made. This type of inductive learning fosters a sense of ownership and interest in the concept discovered. Discovering patterns and making conjectures can motivate learning about proof.

Factoring the Difference of Two Squares

This example illustrates inductive, or discovery, learning. The concept to be developed is factoring the difference of two squares. In later modules, lessons that discover calculus concepts are developed.

The procedure we will use to discover patterns is

• Explore several related examples
• Describe verbally the pattern of the result
• Predict more results
• Test the prediction
• Extend the type of examples explored
• Generalize

Explore Factoring x² – 4

To factor x² – 4,

• Clear the Home Screen and all one-letter variables with the New Problem command by pressing
• Paste the factor( command to the Edit Line by pressing
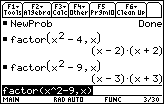
• Complete the command factor(x^2–4,x) by pressing

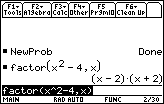
The factors of x² – 4 are x – 2 and x + 2.

Explore Factoring x² – 9

• Edit the expression in the Edit Line by pressing to move the cursor to the end of the expression and then by pressing to erase the 4 and replace it with 9
• Press to see the result

You may want to factor other examples of the difference of two squares to determine a pattern relating the original expression and its factors. After a few examples, you will probably notice a pattern. Can you predict the result of the next two commands before entering them? Write your predictions down before entering the commands into the calculator.

Explore by Factoring Other Examples

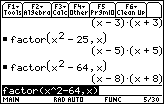
• factor(x^2 – 25, x)
• factor(x^2 – 64, x)

Describe the Pattern Verbally

2.3.1 When you see the pattern, describe it verbally and express it with an algebraic expression. Click here for the answer.

Predict the Pattern of the Factors of The Difference of Two Squares

2.3.2 Predict the factors of x² – a² . Click here for the answer.

Test the Prediction

2.3.3 Check your prediction.

• Factor x² – a² by using the factor( command.

  Remember "a" is an ALPHA feature above the key. Click here for the answer.

Extend and Check

2.3.4 Predict the factors of x² – 5. Click here for the answer.

2.3.5 Factor x² – 5 by using the factor( command. Click here for the answer.

Generalize

2.3.6 Predict the factors of x² – a . Click here for the answer.

Factoring Over Different Number Sets The command factor(x^2–5,x) gives a different result than factor(x^2–5). The first command factors over the real numbers. The second command factors over the rational numbers. The command cfactor( factors over the complex numbers. This command is found in the F2:Algebra, A:Complex submenu. You could also type the entire command or add a "c" in front of the factor( command.

2.3.7 Try cfactor(x^2+4,x).

Click here for the answer.

Binomial Expansion

You will now explore expanding expressions like (x + 1)ⁿ, which are called binomial expansions. The pattern of the powers of the variable in the expansion is

We want to find the values of the coefficients. In the following exploration you should look for a pattern in these coefficients and how they relate to the power of the expansion, n.

• Start fresh by selecting NewProb from the Clean Up menu on the Home screen by pressing

The Expand( Command

To explore binomial expansions, you will use the expand( command, which is in the Algebra menu of the Home screen.

Explore the Expansion of (x + 1)²

To expand the expression (x + 1)²,

• Paste the expand( command to the Edit Line by pressing
• Complete the command expand ((x + 1)²) by pressing

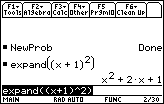
When n = 2, the coefficients of the expansion are 1, 2, 1.

Explore the Expansion of (x + 1)³

• Edit the expression in the Edit Line to cube the binomial by pressing

When n = 3, the coefficients are 1, 3, 3, 1.

Explore the Expansion of (x + 1)⁴ and the Expansion of (x + 1)⁵

• Raise the binomial to the fourth power with
• Edit the expression in the Edit Line to raise the binomial to the fifth power

When n = 4, the coefficients are 1, 4, 6, 4, 1.

When n = 5, the coefficients are 1, 5, 10, 10, 5, 1.

Describe the Pattern

The coefficients found by expanding (x + 1)ⁿ, when n = 2,3,4,5 are shown in the respective rows of the triangle below.

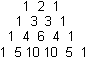
2.3.8 Describe the pattern shown in the triangle above. Click here for the answer.

You can expand the triangle, both below and above the existing rows, and use the new rows to determine the coefficients of other expansions of (x + 1)ⁿ .

Predict (x + 1)⁶ and Confirm

2.3.9 Use the next line below the triangle shown above to predict (x + 1)⁶ and then check your answer with the expand( command. Click here for the answer.

We will not extend and generalize this topic at this time.

Discovery Learning

Using the TI-89, you are able to see the results of many binomial expansions more quickly than would be possible with only paper and pencil. This facilitates inductive learning. The Explore, Describe, Predict, Confirm, Extend, and Generalize procedure is a more active form of learning than reading or listening. Hopefully, when you use this procedure, you have more of a sense of discovering the theorem, rather than just being told the result.

The Expand( Command The expand( command, which is found on the Home screen's Algebra menu, can be used to expand other expressions.

2.3.10 Expand the product (x + 1) (x² – x + 1) by using the expand( command.

Click here for the answer.