Lesson 27.1 introduced polar coordinates and Lesson 27.2 investigated the graphs of polar equations. This lesson explores finding the area bounded by polar graphs.

Finding the Area Bounded by Polar Graphs

The area of the region between the origin and the curve r = f( ) for is given by the definite integral

.

This definite integral can be used to find the area of the region enclosed by the cardioid
r = 2(1 + cos ).

The complete graph of this function is plotted using the interval , so the area is given by the definite integral

.

The integral may be evaluated on your TI-83.

• Enter 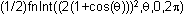on the Home screen.

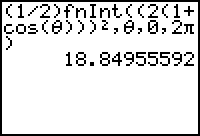
The area enclosed by the cardioid is approximately 18.8496 square units. The exact area is 6 square units.

27.3.1 Find the area enclosed by the curve r = 2 on the interval . Click here for the answer.

Finding the Area Between Two Polar Curves

The area bounded by two polar curves where on the interval is given by

.

This definite integral can be used to find the area that lies inside the circle r = 1 and outside the cardioid r = 1 – cos .

First illustrate the area by graphing both curves.

• Set r1 = 1.
• Set r2 = 1 – cos( ).
• Use a [0, 2 , /24] x [-4, 4, 1] x [-3, 3, 1] viewing window

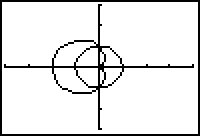
The area inside the circle and outside the cardioid lies in the first and fourth quadrants.

To find the area between the curves you need to know the points of intersection of the curves. The TI-83 can display coordinates in Polar form.

• Press [FORMAT], which is above , to open the Format menu and select PolarGC (Polar Graphing Coordinates).

• Return to the graph and Trace to the first point of intersection.

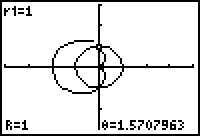
The first point of intersection occurs when .

• Trace to find the second point of intersection.

The second point of intersection occurs when .

In most cases, we can find all of the intersections by looking at appropriate graphs. What we cannot necessarily find as easily are the polar coordinates corresponding to the point of intersection for each of the two functions. Because of the infinite multiple representation problem, one point of intersection might be on the two different curves for different values of . Even though one point might be on both curves (a point of intersection), it might be on the two curves for different values of , and that can cause complications when we try to find areas this way.

The two points of intersection are at and . However, the values of in the interval correspond to the parts of the graphs that are in quadrants II and III. We want the area bounded by the graphs in quadrants IV and I. In order to obtain the proper limits of integration notice that the polar point is the same as so the desired area is found by letting range from - /2 to /2.

The definite integral that gives the area is

.

• Enter .

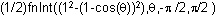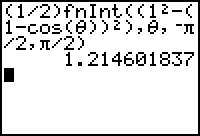
The area is approximately 1.215 square units.

27.3.2 Find the area of the region inside the circle r = 3 sin and outside the cardoid r = 1 + sin . Click here for the answer.