It is often useful to find a vector function that models the path of a projectile. Such a function can yield the particle's position at time t as well as its velocity and acceleration. This lesson will explore finding the function that models the path of such an object given some initial information.

Finding the Position Vector

A projectile is fired from ground level. If the starting point for the projectile is considered to be the origin and if air resistance is neglected, the position vector for the projectile at time t is

where v₀ is the initial velocity of the projectile, is the angle from the horizontal at which the projectile is fired and g is the acceleration due to gravity. When t is measured in seconds and distance is measured in feet, the acceleration due to gravity is given by g = 32 ft/sec each second. If distance is measured in meters, g = 9.8 m/sec².

The position vector can also be represented with the corresponding parametric equations

.

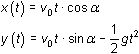A Specific Example

Suppose a projectile is fired at an angle of = 20° from the horizontal with an initial velocity of 180 ft/sec. Graph the path of the projectile using 32 ft/sec² for g.

• Select Degree in the Mode menu.

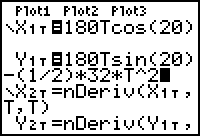
• Set X_1T = 180*T*cos(20).
• Set Y_1T = 180*T*sin(20) - (1/2)*32*T^2.
• Unselect X_2T and Y_2T.
• Unselect X_3T and Y_3T.

• Enter the following window values: [0, 5, 0.1] x [0, 800, 100] x [-50, 100, 10].
• Graph the path of the object.

26.3.1 Use the trace key to approximate when the projectile reaches its highest point and estimate the position vector at the highest point. Click here for the answer.

Recalling Previous Functions

If you have not cleared the variables X_2T, Y_2T and X_3T, Y_3T since Lesson 26.2, these variables should still be defined as the velocity and acceleration vectors for the position vector stored in X_1T and Y_1T. If you have cleared these variables, redefine them as they were defined in Lesson 26.2.

• Set X_2T = nDeriv(X_1T,T,T).
• Set Y_2T = nDeriv(Y_1T,T,T).
• Set X_3T = nDeriv(X_2T,T,T).
• Set Y_3T = nDeriv(Y_2T,T,T).

26.3.2 Select the velocity parametric equations. Evaluate the velocity vector at the value of t when the projectile reaches its highest point. Interpret the meaning of this vector in terms of the projectile motion.

Click here for the answer.

The vertical speed of a projectile when it reaches its highest point is always zero, but in the last problem, our answer was slightly different from zero. That is because we used t = 1.9 seconds for our computation, and that is not the time that the projectile actually reaches its peak. Using a smaller value of Tstep would allow allow us to find the time at the peak more accurately, but it would also result in the graphs being displayed more slowly.

26.3.3 Select the acceleration parametric equations. Evaluate the acceleration vector at several values of t. Interpret the meaning of this vector in terms of the projectile motion.

Click here for the answer.