In this lesson you will learn to define vectors, use different notations to describe vectors, and perform two types of vector multiplication: scalar multiplication and dot products. Unit vectors will be discussed and vector projections will be illustrated.

Defining Vectors

Quantities that have both magnitude and direction are called vectors and are often represented by directed line segments, as illustrated below.

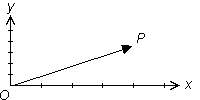
The vector shown has an initial point at O and a terminal point at P.

Representing Vectors

Any two-dimensional vector may be represented as a directed line segment with initial point at the origin, and vectors that have an initial point at the origin can be represented with the coordinates of the tip of the arrow. For example, a vector that goes from the origin to the point (3, 2) is represented with the notation <3, 2>. For the vector v = <a, b>, a and b are called the coordinates or components of v, or more specifically, the x-coordinate and y-coordinate of v.

Unit Vectors i and j

The vector i is one unit long and points along the positive x-axis and the vector j is one unit long and points along the positive y-axis. Because the vectors i and j are each one unit long they are called unit vectors. Both i and j are shown below along with the vector a, which has terminal point (3, 2).

Notice that a, i, and j are written in bold to signify that they are vectors.

Representing Vectors using i and j

A vector can also be represented using the unit vectors i and j. For example, the vector a = <3, 2> can be written as

The Length of a Vector

The length or magnitude of any vector a = <x, y> is

.

The length of a = <3, 2> is units.

Scalar Multiplication of Vectors

Letting c represent a

A scalar is a real number. It has magnitude but no direction.

scalar and a represent a vector, the scalar multiple ca of a is

1. a vector whose length is |c| times that of the length of a and
2. a vector whose direction is
   1. the same as a if c is positive and
   2. the opposite direction from a if c is negative.

The coordinates of ca are found by multiplying each coordinate of a by c.

26.1.1 What is the scalar multiple 2 <3, -1>? Click here for the answer.

A Unit Vector

Any vector whose magnitude is one is called a unit vector. It is often useful to find the unit vector that points in the same direction as a given vector a. In order to find this vector, each component of a is divided by the magnitude of a.

To determine a unit vector that points in the same direction as a = <3,2>, find the magnitude of a and then multiply the vector by the reciprocal of the magnitude.

The magnitude of a is , so the unit vector is

.

26.1.2 Determine a unit vector that points in the same direction as a = <-2, 5>. Click here for the answer.

Dot Products of Vectors

There is a second type of multiplication involving vectors called the dot product. Dot products are widely used in physics. For example, they are used to calculate the work done by a force acting on an object.

The dot product of the two vectors and is defined to be

That is, the dot product of two vectors is the sum of the products of their corresponding components. Notice that the result of the dot product of two vectors is a real number, not a vector.

26.1.3 Let and . Compute the dot product a · b. Click here for the answer.

An Alternate Definition of Dot Product

The dot product can also be defined as the product of the magnitude of a, the magnitude of b, and the cosine of the angle between a and b. If is the angle between a and b

.

Projecting One Vector onto Another Vector

A projection can be obtained by dropping a perpendicular from the head of one vector to the line containing the other. When the two vectors have the same initial point, the projection of b onto a

1. is parallel to a and
2. has the length of the projection onto b.

  

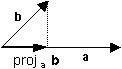
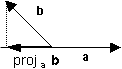
The Component of b Along a

The magnitude of the projection of b onto a, |proj_ab|, is also called the component of b along a. It is denoted as comp_ab and is equal to the magnitude of b times the cosine of , the angle between a and b. Because , comp_ab is also equal to the dot product of a and b divided by the magnitude of a. Symbolically,

.

26.1.4 Find comp_ab and comp_ba if and . Click here for the answer.