The arc length of a segment of a curve was found in Module 19. This lesson will investigate finding the arc length of a parametric curve by using a function that you will define and store in the Y= editor.

Arc Length of a Parametric Curve

The length of a parametric curve between t = a and t = b is given by the definite integral

The TI-83 can be used to find the length of the parametric curve below for .

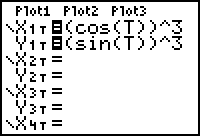
Enter the functions into the Y= editor.

• Set X_1T = (cos(T))^3.
• Set Y_1T = (sin(T))^3.

A Function to Compute Arc Length

Because you probably do not want to enter the complicated integral each time, an arc length function can be defined in a set of parametric equations and used for curves defined by X_1T and Y_1T.

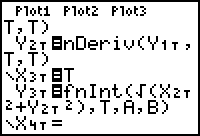
• Set X_2T = nDeriv(X_1T,T,T). Press to paste X_1T into the line.
• Set Y_2T = nDeriv(Y_1T,T,T). Press to paste Y_1T into the line.

• Define X_3T = T. (This procedure will work if you leave X_3T blank.)
• Define

• Return to the Home screen and store 0 in A and /2 in B.

• Enter Y_3T on the Home screen to compute the arc length.

The arc length of the curve x = cos³t, y = sin³t between t = 0 and t = /2 appears to be about 1.5 units.

Remember that nDeriv( is only approximate. If the functions are simple enough you can use symbolic derivatives to possibly improve accuracy.

25.3.1 Find the length of this parametric curve for . You should only need to change the values stored in A and B and then enter Y_3T again on the Home screen.

Click here for the answer.

The graph of the parametric equations x = cos³t, y = sin³t will show why both arc lengths are the same.

• Unselect the second and third pairs of parametric equations in the Y= editor and graph the first parametric equation in a [0, 2 , 0.1] x [-3, 3, 1] x [-2, 2, 1] window.

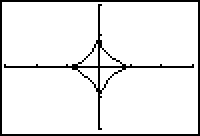
The graph is called a hypocycloid. The symmetry of the graph shows why the arc lengths are the same for and for .

The Length of the Spiral of Archimedes

The Spiral of Archimedes is defined by the parametric equations x = tcos(t), y = tsin(t).

Find the length of the spiral for .

The parametric equations in X_1T and Y_1T should be changed to the new equations, however the derivatives and integral in the other parametric equations should remain the same.

• Define X_1T = T · cos(T).
• Define Y_1T = T · sin(T).

• Store 0 in A and 20 in B.
• Enter Y_3T on the Home screen.

The approximate arc length is 202.095 units. This result is difficult to obtain with pencil and paper.

Illustrating the Spiral of Archimedes

• Graph the spiral in a [0, 20, 0.1] x [-30, 30, 10] x [-30, 30, 10] window.

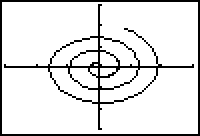
25.3.2 Find the length of the spiral for . Click here for the answer.