Module 25 - Parametric Equations

Module 25 - Parametric Equations

Introduction | Lesson 1 | Lesson 2 | Lesson 3 | Self-Test

Lesson 25.2: Chain Rule for Parametric Equations

This lesson investigates the procedure to find derivatives, such as , , and , for parametric equations x = f(t), y = g(t).

The Chain Rule

Suppose a curve is defined by the parametric equations

x = f(t)

y = g(t)

The Chain Rule states that the derivative for the parametric curve is the ratio of to . Symbolically,

Finding First Derivatives

The values of the derivatives dy/dt, dx/dt, and dy/dx for a set of parametric equations can be found using the TI-83. Suppose you wish to find the values of the derivatives when t = 0.5 for the parametric equations

x(t) = sec t
y(t) = tan t

Recall that and that dy/dt represents the rate of change of y with respect to t, dx/dt represents the rate of change of x with respect to t, and dy/dx represents the rate of change of y with respect to x.

Define X_1T =1/cos(T).
Define Y_1T = tan(T).

Finding Derivatives from a Graph

The derivatives at a point on the graph of a parametric curve can be found by using the derivative features of the CALC menu on the Graph screen.

Set the Window values to [0, 2 , 0.1] x [-3, 3, 1] x [-5, 5, 1] and graph the parametric equations.

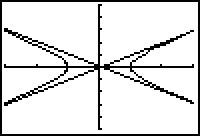
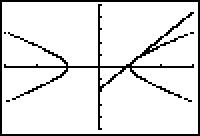
The graph is a hyperbola. The two diagonal lines are not part of the graph. The two lines are similar to the vertical lines that often appear in graphs of functions that have vertical asymptotes.

Using Dot Style

If you graph the parametric equations using Dot style the diagonal lines will not be displayed.

When you graph using Dot style you may want to make the value of Tstep smaller to increase the resolution of the graph but smaller values of Tstep also increase the time required to graph the curve.

Dot graphing style can be selected by moving the cursor to the icon on the left of X_1T and pressing until appears.

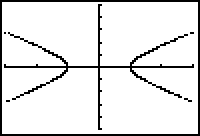
Set Tstep to 0.01 and redraw the graph in Dot graphing style.

Open the CALC menu by pressing [CALC].

Select "2:dy/dx."

The calculator returns to the graph.

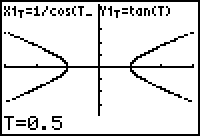
Type 0.5 to enter the value for T.

Press to calculate the derivative.

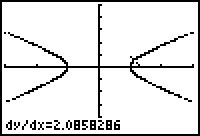
The value of dy/dx at t = 0.5 is approximately 2.0858. That is, the y-values are increasing about 2.0858 times as fast as the x-values.

25.2.1 Use the CALC menu to find the value of dy/dt and dx/dt at t = 0.5. Do these values satisfy the Chain Rule for parametric equations? Click here for the answer.

Finding the Equation of the Tangent Line

The slope of the tangent line is dy/dx 2.0858. To find the x and y coordinates of the point on the curve when t = 0.5, use the value feature in the CALC menu.

Open the CALC menu and select "1:value."
Enter 0.5 for T.

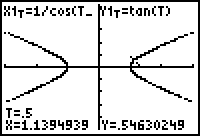
The coordinates of the point on the curve when t = 0.5 are approximately (1.1395, 0.5463). Using the point just found and the value of dy/dx for the slope of the line, the equation of the tangent line is

y = 2.0858(x - 1.1395) + 0.5463.

Graph this function parametrically.

Enter X_2T = T.
Enter Y_2T = 2.0858(T - 1.1395) + 0.5463.

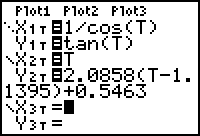
Display the graphs of the hyperbola and the tangent line at t = 0.5.

25.2.2 Graph the curve given by the parametric equations below and find the equation of the tangent line to the curve when t = 2.

x = t - sin(t)
y = 1 - cos(t)

Click here for the answer.

< Back | Next >