In this lesson the graphs of various families of parametric curves are explored. Look for patterns in the curves as the parameters in the equations are changed.

Graphing Families of Parametric Curves

Parametric equations often represent interesting graphs that cannot be graphed using the Function mode.

A Cycloid

Imagine you are stopped at an intersection and a bicycle crosses the intersection in front of you. A reflector is attached to the rim of the bicycle tire. The TI-83 can display the path that the reflector will take.

• Select parametric and radian mode in the Mode screen.

• Enter the following parametric equations:

X_1T = T - sin(T)

Y_1T = 1 - cos(T)

• Enter the following viewing window:

[0, 6 , 0.1] x [0, 6 , 1] x [-5, 7, 1]

• Display the graph.

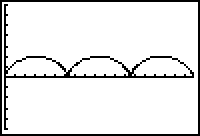
The graph illustrates the path the reflector would follow as the bicycle wheel goes through three revolutions. The curve is called a cycloid.

The equations for a general cycloid are

25.1.1 In the previous example the value of a was 1. Predict the effect of changing the value of a to 2. Check your prediction with your TI-83. Click here for the answer.

25.1.2 How is the value of a related to the bicycle? Click here for the answer.

Epicycloid

Imagine the tire in the cycloid problem rolls around another circle rather than along level ground.

If the radius of the tire is A and the radius of the large circle is B, the following parametric equations will show the path.

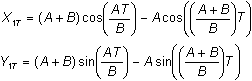
• Enter the equations in the Y= editor.

Suppose the radius of the tire is 1 unit and the radius of the large circle is 5 units.

• Return to the Home screen and store 1 in A and 5 in B.

• Graph in a [0,10 , 0.1] x [-15,15,1] x [-10,10,1] window.

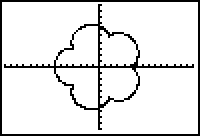
This graph is called an epicycloid and this particular one has 5 "petals."

25.1.3 Graph the epicycloid when the radius of the tire is 2 units and the radius of the large circle is 7 units. How many revolutions of the tire are completed before the reflector returns to its starting point? Click here for the answer.